电话:0551-63600808-8207
nnt 时间:2021-01-11 阅读:()
邮箱:wshuang@ustc.
edu.
cn王双老师§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福散射公式()2224012144sin/2dZedEσπεθ=卢瑟福散射公式表征了α粒子散射到θ角方向上单位立体角内,每个原子的有效散射截面.
反映了散射到θ角方向上单位立体角内的概率.
ddσ称为微分散射截面,其量纲是面积.
§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福散射公式dσtθSndndndNStdNtdnSSσσΣ===α粒子散射到θ角方向上锥面立体角d内的概率散射到θ角方向上单位立体角内的概率()2224012144sin/2dndZeNtNtnddEσπεθ==§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福散射公式[例1.
2]设α粒子是钋源放射的,能量为5.
3MeV,散射体为金箔,厚为1μm,ρ=1.
93*104kg·m-3,Z=79,A=197,试求:(1)α粒子通过金箔在60°角方向的卢瑟福微分散射截面;(2)散射角大于90°的所有α粒子占全部入射粒子的百分比.
222460022240224232()12144sin/22144sin/22791(1.
44eVnm)45.
3MeVsin301.
8410cmdZedEeZEθσθπεθπεθ=°==*=*°=*222222022250144sin/248.
51044AdnzZedNtnENtezZAEπππππεθρππε===*∫∫[解](1)60°角方向的卢瑟福微分散射截面:(2)散射角大于90°的所有α粒子占全部入射粒子的百分比:201.
444eeVnmπε=复合常数H.
GEIGERandE.
MARSDEN,TheLawsofDeflexionofaParticlesthroughLargeAngles,PhilosophicalMagazine,Series6,Volume25,Number148,April1913(1)随角度的变化关系;(2)随散射体厚度的变化关系;(3)随入射粒子速度(能量)的变化关系;(4)随散射材料的原子量的变化关系.
§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证()222401244sin/2ZeddnnNtEπεθ=AngleθScintillationsperminute.
1--------sin4θdn*(sin4θ/2)Withoutfoil.
Withfoil.
Correctedforeffectwithoutfoil.
Correctedfordecay,dn.
1500.
24.
954.
756.
951.
156.
01352.
68.
35.
78.
351.
386.
11203.
810.
36.
59.
51.
795.
31050.
610.
610.
014.
62.
535.
8750.
028.
628.
641.
97.
255.
8600.
369.
268.
910116.
06.
3(1)随角度的变化关系()2224012sin/2.
44ZednnNtdconstEθπε==§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证(2)随散射体厚度的变化关系§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证()222401244sin/2ZeddnnNtEtπεθ=∝I.
NumberofsheetsofmicaII.
RangeRofαparticlesafterleavingmicaIII.
Relativevaluesof1/ν4IV.
Numberdnofscintillationsperminute.
V.
dn*v405.
51.
024.
72514.
761.
2129.
02424.
051.
5033.
42233.
321.
91442342.
512.
84812851.
844.
321012361.
049.
2225528§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证(3)随入射粒子速度的变化关系()22244012.
42sin/2ZeddnvnNtconstmπεθ==I.
Substance.
II.
Atomicweight.
A.
III.
Airequivalentincm.
IV.
NumberofscintillationsperminutecorrectedfordecayV.
Numberdnofscintillationspercm.
airequivalent.
VI.
A3/2.
VII.
dn/A3/2.
Gold.
.
.
.
.
.
.
1970.
22913358127700.
21Tin.
1190.
44111927013000.
21Silver.
.
.
.
.
.
107.
90.
26251.
719811200.
18Copper.
.
.
.
63.
60.
616711155070.
23Aluminium.
27.
12.
057134.
61410.
24§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证(4)随散射材料的原子量A的变化关系()22224012.
44sin/2dnednNtconstZEπεθ==§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证新物理量:原子核电荷数ZJ.
Chadwick(1891-1974)1920年,JamesChadwick直接测量了Cu,Ag和Pt的Z()222401244sin/2eddnnZNtEπεθ=发现在1.
5%的误差范围内与原子序数(在元素周期表上的排序)相同.
Mendeleev's1871periodictableD.
Mendeleev(1834-1907)§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正假设靶原子核的反冲(有限大小的M)(1)忽略核外电子的作用(me>mα);(4)忽略了多次散射.
卢瑟福散射公式用到质心系仍成立,转换到实验室系222222202cos1sin()1244sin(1cos)1sin2LLLLLLLLmMdZedmEMθθσθθπεθθ+=*+§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正E0EθL靶原子核的反冲(有限大小的M)散射α粒子的能量2220cossinLLmMmEEmMθθ+=+当θ很小时,E和E0差别不大;当θ>90°(背散射),E和E0差别较大.
极限情况:θ180°002~1MmmEEEMmM→+§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正例如:E0=5MeV,m=4u.
对于C元素,24~151.
6712EMeVMeV**=对于Si元素,24~153.
5728EMeVMeV**=Rutherford-Backscattering-Spectrometry应用:卢瑟福背散射谱仪§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正小角偏差(1)核外电子的屏蔽效应;瞄准距离b很大22bctgDθ=(2)多次散射导致小角增强.
大角偏差思考题:如何测量180°附近的α粒子散射双原子散射模型来解释.
1980年代,发现在180°背散射附近十分之几度范围内,非晶和多晶薄箔的散射实验值比用卢瑟福公式算出的大,通常可以增大1~2倍.
§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正原子核的大小()222401244sin/2ZeddnnNtEπεθ=固定θ角,dn∝1/E2dn∝1/E202242bbEctgDZeθπε==固定θ角,E越大b越小.
小到一定程度,α粒子会进入原子核,散射关系发生突变(强核力起作用).
突变点的α粒子正好掠过原子核表面,最近距离rm即近似为原子核半径.
§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正原子核的大小dn∝1/E2角动量守恒22200112224mmZeEmvmvrπε==+0mmmvbmvr=能量守恒0mmvvbr=022mvDctgrθ=得(一元二次方程,取"+"解)20121csc1csc22422mDZerEθθπε=+=+§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正原子核的大小dn∝1/E2图中的例子,转折点发生在25MeV201csc42meZrEθπε=+7911.
44125sin30eVnmMeV=+°14~1.
3610m*14~10m10~10m§1.
3.
2卢瑟福原子模型和散射公式--截面的进一步讨论dσtdndndnNStdS∝n单位时间内在θ角方向dΩ立体角内探测到的被散射的粒子数dnθ散射中心数目单位面积入射粒子数强度探测器所张立体角§1.
3.
2卢瑟福原子模型和散射公式--截面的进一步讨论dσtdndndnANStdANtndS==n单位时间内在θ角方向dΩ立体角内探测到的被散射的粒子数dnθdnANtdn=一个粒子被散射到θ角方向dΩ立体角内的概率§1.
3.
2卢瑟福原子模型和散射公式--截面的进一步讨论两个因子:因子1:Nt散射体的原子数密度和厚度.
因子2:1dndAnNtddσ==θ**=角方向d立体角内的散射粒子数入射粒子数单位面积的靶原子数探测器所张立体角表示单位面积内垂直入射一个粒子(n=1)时,被这个面积内的一个靶原子(Nt=1)散射到θ角方向单位立体角内的概率.
该因子与入射粒子数、靶的形状和靶粒子数均无关,只决定于发生相互作用的粒子与散射中心的性质以及它们之间相互作用的动力学性质.
§1.
3.
2卢瑟福原子模型和散射公式--截面的进一步讨论dndNtdndσ=ddσ()2224012144sin/2dZedEσπεθ=微观相互作用机制宏观可观测量α粒子与原子的库仑散射过程总散射截面或积分截面0()()2sinddddddπσθσθσπθθ==∫∫§1.
3.
3卢瑟福原子模型的困难确定的原子大小14~10m10~10m以氢原子为例,假设原子核静止(M>>me),核外电子在原子核的库仑场中以半径r做圆周运动.
则有22204vemrrπε=电子动能22011224eTmvrπε==电子在库仑场中的势能(r→∞,V=0)204eVrπε=电子的总能量2220001124424eeeETVrrrπεπεπε对r没有限制,但实际情况是原子大小约为10-10m.
§1.
3.
3卢瑟福原子模型的困难原子的稳定性做圆周运动的核外电子辐射电磁波而损失能量.
20124eErπε=E↓r↓原子"塌缩"§1.
3.
3卢瑟福原子模型的困难[例1.
3]设H原子中电子绕原子核作圆周运动,原子的初始半径为10-10m,请由经典电磁理论估计电子落到原子核上的时间.
[解]由拉莫尔公式,一个以加速度a运动的带电粒子的辐射功率为:而,由此由,得圆周运动的加速度,有因此可得22306dEeaPdtcπε==dEdEdrdtdrdt=drdEdEdtdrdt=20124eErπε=201124dEedrrπε=222014vearmrπε==2222304134dredtmrcπε=222302434dtmrcdreπε=20233100241104RtdtmRcseπε==≈∫§1.
3.
3卢瑟福原子模型的困难原子的辐射特性原子辐射电磁波的频率应等于电子做圆周运动周期的频率,以氢原子为例:2vfrπ=14~10m10~10m204evmrπε=30124efmrππε=连续的原子光谱分立的原子光谱§1.
3.
3卢瑟福原子模型的困难Wemayregardthepresentstateoftheuniverseastheeffectofitspastandthecauseofitsfuture.
Anintellectwhichatacertainmomentwouldknowallforcesthatsetnatureinmotion,andallpositionsofallitemsofwhichnatureiscomposed,ifthisintellectwerealsovastenoughtosubmitthesedatatoanalysis,itwouldembraceinasingleformulathemovementsofthegreatestbodiesoftheuniverseandthoseofthetiniestatom;forsuchanintellectnothingwouldbeuncertainandthefuturejustlikethepastwouldbepresentbeforeitseyes.
—PierreSimonLaplaceScientificdeterminism19世纪末经典物理的困难黑体辐射、光电效应、原子的分立线光谱等不透明物体反射吸收透射transmissionτ,absorptionα,andreflectionρthermalradiationofabody§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射§1.
4能量量子化和光的波粒二象性理想黑体§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射吸收全部辐射(100%吸收)的物体称为理想黑体.
热平衡时,吸收与辐射达到平衡.
辐射本领1879年,J.
Stefan建立了黑体单位面积的辐射本领与温度关系的经验公式.
4RTσ=(Stefan公式)(Stefan常数)8245.
670310WmKσ=*1884年,Boltzmann推导了这一结果.
吸收的同时,对外辐射电磁波,即黑体辐射.
黑体辐射的波长分布§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射()Rdλλ单位面积上发射波长在λ~λ+dλ电磁辐射的辐射本领.
()Rλ维恩(W.
Wien)位移定律§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射3=2.
89810mTmKλ=*常数§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射太阳的黑体辐射谱§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射黑体的辐射本领R取决于腔体内热平衡的辐射场的能量密度u.
1()()4Rcuλλ=14Rcu=能量密度u,是腔体内单位体积的辐射能.
能量密度u(λ),是腔体内单位体积内,波长在λ~λ+dλ的辐射能.
,()RRλ实验测量理论计算,()uuλ§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射波长在λ~λ+dλ间隔内,腔中单位体积的驻波电磁场的振荡模式的数目:经典理论计算()uλ4()8nλπλ=将这些振荡看作一维谐振子,在热平衡下,服从Maxwell-Boltzmann分布,其能量分布函数/()BEkTfECe=立方体腔中的振荡模式(C是归一化常数,kB是Boltzmann常数)振子(振荡模式)的平均能量/00()BEkTBEEfEdECEedEkT∞∞==∫∫§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射经典理论计算()uλ4()()8BBunkTkTλλπλ==Rayleigh-Jeans公式当λ→0,u(λ)→∞MaxPlanckApril23,1858–October4,1947TheNobelPrizeinPhysics1918Planck,Max.
(1900).
"EntropyandTemperatureofRadiantHeat.
"AnnalenderPhysik,vol.
1.
no4.
April,pg.
719-37.
§1.
4.
1黑体辐射与Planck的量子假说—量子假说1900年,普朗克宣称经验公式251/()1ccueλλλ=MaxPlanckApril23,1858–October4,1947TheNobelPrizeinPhysics1918Planck,Max.
(1901).
"OntheLawofDistributionofEnergyintheNormalSpectrum".
AnnalenderPhysik,vol.
4,p.
5531901年,普朗克进一步作了一点奇怪的假设,推导出了公式.
假设谐振子的能量不是连续的,即能量只能取一个最小单元的整数倍.
普朗克量子假说,0,1,2,3,Ennε==hεν=不同频率谐振的能量子h是一个普适的常数,现在称为普朗克常数.
§1.
4.
1黑体辐射与Planck的量子假说—量子假说h=6.
626*10-34Js能量分布函数//nBBEkTnkTnfCeCeε==归一化常数C/01BnkTnCeε∞==∑/1BkTCeε=振子(振荡模式)的平均能量/00nBEkTnnnnnEEfECe∞∞====∑∑/1BhkTheνν=154//8()()811BBhckThckThchcunEeeλλλπλλλπλ===能量密度251/()1ccueλλλ=经验公式§1.
4.
1黑体辐射与Planck的量子假说—量子假说5/8()1BhckThcueλπλλ=§1.
4.
1黑体辐射与Planck的量子假说—量子假说长波极限:设/BxhckTλ=是小量/11/1/BhckTBBehckThckTλλλ548()8/BBhcukThckTπλλπλλ≈=
edu.
cn王双老师§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福散射公式()2224012144sin/2dZedEσπεθ=卢瑟福散射公式表征了α粒子散射到θ角方向上单位立体角内,每个原子的有效散射截面.
反映了散射到θ角方向上单位立体角内的概率.
ddσ称为微分散射截面,其量纲是面积.
§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福散射公式dσtθSndndndNStdNtdnSSσσΣ===α粒子散射到θ角方向上锥面立体角d内的概率散射到θ角方向上单位立体角内的概率()2224012144sin/2dndZeNtNtnddEσπεθ==§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福散射公式[例1.
2]设α粒子是钋源放射的,能量为5.
3MeV,散射体为金箔,厚为1μm,ρ=1.
93*104kg·m-3,Z=79,A=197,试求:(1)α粒子通过金箔在60°角方向的卢瑟福微分散射截面;(2)散射角大于90°的所有α粒子占全部入射粒子的百分比.
222460022240224232()12144sin/22144sin/22791(1.
44eVnm)45.
3MeVsin301.
8410cmdZedEeZEθσθπεθπεθ=°==*=*°=*222222022250144sin/248.
51044AdnzZedNtnENtezZAEπππππεθρππε===*∫∫[解](1)60°角方向的卢瑟福微分散射截面:(2)散射角大于90°的所有α粒子占全部入射粒子的百分比:201.
444eeVnmπε=复合常数H.
GEIGERandE.
MARSDEN,TheLawsofDeflexionofaParticlesthroughLargeAngles,PhilosophicalMagazine,Series6,Volume25,Number148,April1913(1)随角度的变化关系;(2)随散射体厚度的变化关系;(3)随入射粒子速度(能量)的变化关系;(4)随散射材料的原子量的变化关系.
§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证()222401244sin/2ZeddnnNtEπεθ=AngleθScintillationsperminute.
1--------sin4θdn*(sin4θ/2)Withoutfoil.
Withfoil.
Correctedforeffectwithoutfoil.
Correctedfordecay,dn.
1500.
24.
954.
756.
951.
156.
01352.
68.
35.
78.
351.
386.
11203.
810.
36.
59.
51.
795.
31050.
610.
610.
014.
62.
535.
8750.
028.
628.
641.
97.
255.
8600.
369.
268.
910116.
06.
3(1)随角度的变化关系()2224012sin/2.
44ZednnNtdconstEθπε==§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证(2)随散射体厚度的变化关系§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证()222401244sin/2ZeddnnNtEtπεθ=∝I.
NumberofsheetsofmicaII.
RangeRofαparticlesafterleavingmicaIII.
Relativevaluesof1/ν4IV.
Numberdnofscintillationsperminute.
V.
dn*v405.
51.
024.
72514.
761.
2129.
02424.
051.
5033.
42233.
321.
91442342.
512.
84812851.
844.
321012361.
049.
2225528§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证(3)随入射粒子速度的变化关系()22244012.
42sin/2ZeddnvnNtconstmπεθ==I.
Substance.
II.
Atomicweight.
A.
III.
Airequivalentincm.
IV.
NumberofscintillationsperminutecorrectedfordecayV.
Numberdnofscintillationspercm.
airequivalent.
VI.
A3/2.
VII.
dn/A3/2.
Gold.
.
.
.
.
.
.
1970.
22913358127700.
21Tin.
1190.
44111927013000.
21Silver.
.
.
.
.
.
107.
90.
26251.
719811200.
18Copper.
.
.
.
63.
60.
616711155070.
23Aluminium.
27.
12.
057134.
61410.
24§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证(4)随散射材料的原子量A的变化关系()22224012.
44sin/2dnednNtconstZEπεθ==§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的实验验证新物理量:原子核电荷数ZJ.
Chadwick(1891-1974)1920年,JamesChadwick直接测量了Cu,Ag和Pt的Z()222401244sin/2eddnnZNtEπεθ=发现在1.
5%的误差范围内与原子序数(在元素周期表上的排序)相同.
Mendeleev's1871periodictableD.
Mendeleev(1834-1907)§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正假设靶原子核的反冲(有限大小的M)(1)忽略核外电子的作用(me>mα);(4)忽略了多次散射.
卢瑟福散射公式用到质心系仍成立,转换到实验室系222222202cos1sin()1244sin(1cos)1sin2LLLLLLLLmMdZedmEMθθσθθπεθθ+=*+§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正E0EθL靶原子核的反冲(有限大小的M)散射α粒子的能量2220cossinLLmMmEEmMθθ+=+当θ很小时,E和E0差别不大;当θ>90°(背散射),E和E0差别较大.
极限情况:θ180°002~1MmmEEEMmM→+§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正例如:E0=5MeV,m=4u.
对于C元素,24~151.
6712EMeVMeV**=对于Si元素,24~153.
5728EMeVMeV**=Rutherford-Backscattering-Spectrometry应用:卢瑟福背散射谱仪§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正小角偏差(1)核外电子的屏蔽效应;瞄准距离b很大22bctgDθ=(2)多次散射导致小角增强.
大角偏差思考题:如何测量180°附近的α粒子散射双原子散射模型来解释.
1980年代,发现在180°背散射附近十分之几度范围内,非晶和多晶薄箔的散射实验值比用卢瑟福公式算出的大,通常可以增大1~2倍.
§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正原子核的大小()222401244sin/2ZeddnnNtEπεθ=固定θ角,dn∝1/E2dn∝1/E202242bbEctgDZeθπε==固定θ角,E越大b越小.
小到一定程度,α粒子会进入原子核,散射关系发生突变(强核力起作用).
突变点的α粒子正好掠过原子核表面,最近距离rm即近似为原子核半径.
§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正原子核的大小dn∝1/E2角动量守恒22200112224mmZeEmvmvrπε==+0mmmvbmvr=能量守恒0mmvvbr=022mvDctgrθ=得(一元二次方程,取"+"解)20121csc1csc22422mDZerEθθπε=+=+§1.
3.
2卢瑟福原子模型和散射公式--卢瑟福公式的修正原子核的大小dn∝1/E2图中的例子,转折点发生在25MeV201csc42meZrEθπε=+7911.
44125sin30eVnmMeV=+°14~1.
3610m*14~10m10~10m§1.
3.
2卢瑟福原子模型和散射公式--截面的进一步讨论dσtdndndnNStdS∝n单位时间内在θ角方向dΩ立体角内探测到的被散射的粒子数dnθ散射中心数目单位面积入射粒子数强度探测器所张立体角§1.
3.
2卢瑟福原子模型和散射公式--截面的进一步讨论dσtdndndnANStdANtndS==n单位时间内在θ角方向dΩ立体角内探测到的被散射的粒子数dnθdnANtdn=一个粒子被散射到θ角方向dΩ立体角内的概率§1.
3.
2卢瑟福原子模型和散射公式--截面的进一步讨论两个因子:因子1:Nt散射体的原子数密度和厚度.
因子2:1dndAnNtddσ==θ**=角方向d立体角内的散射粒子数入射粒子数单位面积的靶原子数探测器所张立体角表示单位面积内垂直入射一个粒子(n=1)时,被这个面积内的一个靶原子(Nt=1)散射到θ角方向单位立体角内的概率.
该因子与入射粒子数、靶的形状和靶粒子数均无关,只决定于发生相互作用的粒子与散射中心的性质以及它们之间相互作用的动力学性质.
§1.
3.
2卢瑟福原子模型和散射公式--截面的进一步讨论dndNtdndσ=ddσ()2224012144sin/2dZedEσπεθ=微观相互作用机制宏观可观测量α粒子与原子的库仑散射过程总散射截面或积分截面0()()2sinddddddπσθσθσπθθ==∫∫§1.
3.
3卢瑟福原子模型的困难确定的原子大小14~10m10~10m以氢原子为例,假设原子核静止(M>>me),核外电子在原子核的库仑场中以半径r做圆周运动.
则有22204vemrrπε=电子动能22011224eTmvrπε==电子在库仑场中的势能(r→∞,V=0)204eVrπε=电子的总能量2220001124424eeeETVrrrπεπεπε对r没有限制,但实际情况是原子大小约为10-10m.
§1.
3.
3卢瑟福原子模型的困难原子的稳定性做圆周运动的核外电子辐射电磁波而损失能量.
20124eErπε=E↓r↓原子"塌缩"§1.
3.
3卢瑟福原子模型的困难[例1.
3]设H原子中电子绕原子核作圆周运动,原子的初始半径为10-10m,请由经典电磁理论估计电子落到原子核上的时间.
[解]由拉莫尔公式,一个以加速度a运动的带电粒子的辐射功率为:而,由此由,得圆周运动的加速度,有因此可得22306dEeaPdtcπε==dEdEdrdtdrdt=drdEdEdtdrdt=20124eErπε=201124dEedrrπε=222014vearmrπε==2222304134dredtmrcπε=222302434dtmrcdreπε=20233100241104RtdtmRcseπε==≈∫§1.
3.
3卢瑟福原子模型的困难原子的辐射特性原子辐射电磁波的频率应等于电子做圆周运动周期的频率,以氢原子为例:2vfrπ=14~10m10~10m204evmrπε=30124efmrππε=连续的原子光谱分立的原子光谱§1.
3.
3卢瑟福原子模型的困难Wemayregardthepresentstateoftheuniverseastheeffectofitspastandthecauseofitsfuture.
Anintellectwhichatacertainmomentwouldknowallforcesthatsetnatureinmotion,andallpositionsofallitemsofwhichnatureiscomposed,ifthisintellectwerealsovastenoughtosubmitthesedatatoanalysis,itwouldembraceinasingleformulathemovementsofthegreatestbodiesoftheuniverseandthoseofthetiniestatom;forsuchanintellectnothingwouldbeuncertainandthefuturejustlikethepastwouldbepresentbeforeitseyes.
—PierreSimonLaplaceScientificdeterminism19世纪末经典物理的困难黑体辐射、光电效应、原子的分立线光谱等不透明物体反射吸收透射transmissionτ,absorptionα,andreflectionρthermalradiationofabody§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射§1.
4能量量子化和光的波粒二象性理想黑体§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射吸收全部辐射(100%吸收)的物体称为理想黑体.
热平衡时,吸收与辐射达到平衡.
辐射本领1879年,J.
Stefan建立了黑体单位面积的辐射本领与温度关系的经验公式.
4RTσ=(Stefan公式)(Stefan常数)8245.
670310WmKσ=*1884年,Boltzmann推导了这一结果.
吸收的同时,对外辐射电磁波,即黑体辐射.
黑体辐射的波长分布§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射()Rdλλ单位面积上发射波长在λ~λ+dλ电磁辐射的辐射本领.
()Rλ维恩(W.
Wien)位移定律§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射3=2.
89810mTmKλ=*常数§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射太阳的黑体辐射谱§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射黑体的辐射本领R取决于腔体内热平衡的辐射场的能量密度u.
1()()4Rcuλλ=14Rcu=能量密度u,是腔体内单位体积的辐射能.
能量密度u(λ),是腔体内单位体积内,波长在λ~λ+dλ的辐射能.
,()RRλ实验测量理论计算,()uuλ§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射波长在λ~λ+dλ间隔内,腔中单位体积的驻波电磁场的振荡模式的数目:经典理论计算()uλ4()8nλπλ=将这些振荡看作一维谐振子,在热平衡下,服从Maxwell-Boltzmann分布,其能量分布函数/()BEkTfECe=立方体腔中的振荡模式(C是归一化常数,kB是Boltzmann常数)振子(振荡模式)的平均能量/00()BEkTBEEfEdECEedEkT∞∞==∫∫§1.
4.
1黑体辐射与Planck的量子假说—黑体辐射经典理论计算()uλ4()()8BBunkTkTλλπλ==Rayleigh-Jeans公式当λ→0,u(λ)→∞MaxPlanckApril23,1858–October4,1947TheNobelPrizeinPhysics1918Planck,Max.
(1900).
"EntropyandTemperatureofRadiantHeat.
"AnnalenderPhysik,vol.
1.
no4.
April,pg.
719-37.
§1.
4.
1黑体辐射与Planck的量子假说—量子假说1900年,普朗克宣称经验公式251/()1ccueλλλ=MaxPlanckApril23,1858–October4,1947TheNobelPrizeinPhysics1918Planck,Max.
(1901).
"OntheLawofDistributionofEnergyintheNormalSpectrum".
AnnalenderPhysik,vol.
4,p.
5531901年,普朗克进一步作了一点奇怪的假设,推导出了公式.
假设谐振子的能量不是连续的,即能量只能取一个最小单元的整数倍.
普朗克量子假说,0,1,2,3,Ennε==hεν=不同频率谐振的能量子h是一个普适的常数,现在称为普朗克常数.
§1.
4.
1黑体辐射与Planck的量子假说—量子假说h=6.
626*10-34Js能量分布函数//nBBEkTnkTnfCeCeε==归一化常数C/01BnkTnCeε∞==∑/1BkTCeε=振子(振荡模式)的平均能量/00nBEkTnnnnnEEfECe∞∞====∑∑/1BhkTheνν=154//8()()811BBhckThckThchcunEeeλλλπλλλπλ===能量密度251/()1ccueλλλ=经验公式§1.
4.
1黑体辐射与Planck的量子假说—量子假说5/8()1BhckThcueλπλλ=§1.
4.
1黑体辐射与Planck的量子假说—量子假说长波极限:设/BxhckTλ=是小量/11/1/BhckTBBehckThckTλλλ548()8/BBhcukThckTπλλπλλ≈=
- 电话:0551-63600808-8207相关文档
- 癌症中基因环境的相互作用
- diplopiannt
- 1.5nnt
- cahepucannt
- Methodologicalnnt
- lowestnnt
LayerStack$10.04/月(可选中国香港、日本、新加坡和洛杉矶)高性能AMD EPYC (霄龙)云服务器,
LayerStack(成立于2017年),当前正在9折促销旗下的云服务器,LayerStack的云服务器采用第 3 代 AMD EPYC™ (霄龙) 处理器,DDR4内存和企业级 PCIe Gen 4 NVMe SSD。数据中心可选中国香港、日本、新加坡和洛杉矶!其中中国香港、日本和新加坡分为国际线路和CN2线路,如果选择CN2线路,价格每月要+3.2美元,付款支持paypal,支付宝,信用卡等!...

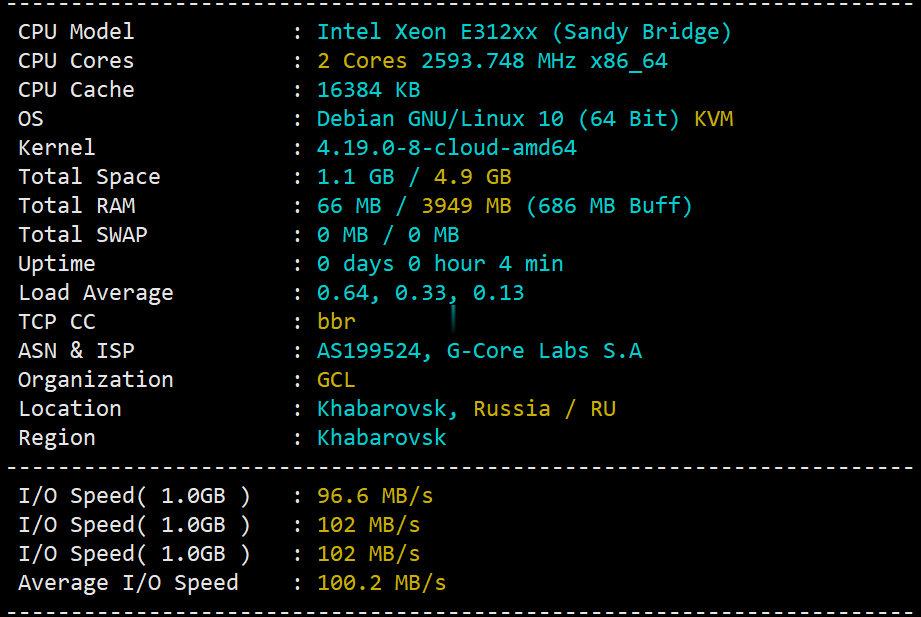
gcorelabs远东khabarovsk伯力Cloud云服务器测评,告诉你gcorelabs云服务器怎么样
说明一下:gcorelabs的俄罗斯远东机房“伯力”既有“Virtual servers”也有“CLOUD SERVICES”,前者是VPS,后者是云服务器,不是一回事;由于平日大家习惯把VPS和云服务器当做一回事儿,所以这里要特别说明一下。本次测评的是gcorelabs的cloud,也就是云服务器。 官方网站:https://gcorelabs.com 支持:数字加密货币、信用卡、PayPal...
搬瓦工VPS:新增荷兰机房“联通”线路的VPS,10Gbps带宽,可在美国cn2gia、日本软银、荷兰“联通”之间随意切换
搬瓦工今天正式对外开卖荷兰阿姆斯特丹机房走联通AS9929高端线路的VPS,官方标注为“NL - China Unicom Amsterdam(ENUL_9)”,三网都走联通高端网络,即使是在欧洲,国内访问也就是飞快。搬瓦工的依旧是10Gbps带宽,可以在美国cn2 gia、日本软银与荷兰AS9929之间免费切换。官方网站:https://bwh81.net优惠码:BWH3HYATVBJW,节约6...
nnt为你推荐
-
广东虚拟主机如果营业执照上的注册地址是属于广东地区对客户的虚拟主机或者域名的地有没有限制?已备案域名查询怎样知道一个网站是不是真的已经备案?网络服务器租用现在网站服务器租赁一年多少钱?免费虚拟主机申请在哪个网站申请的免费虚拟主机可以绑定顶级域名?求高手指点!com域名注册.com的域名注册需要什么证件和资料吗?国内ip代理全国各省代理IP查询ip怎么查询IP地址韩国虚拟主机香港和韩国的虚拟主机哪个比较好?虚拟主机管理系统推荐几个适合windows的免费虚拟主机管理系统合肥虚拟主机虚拟主机哪里买好一些?