numbers98成人网
98成人网 时间:2021-04-11 阅读:()
MoosaeiFixedPointTheoryandApplications2014,2014:98http://www.
fixedpointtheoryandapplications.
com/content/2014/1/98RESEARCHOpenAccessCommonxedpointsforsomegeneralizedcontractionpairsinconvexmetricspacesMohammadMoosaei**Correspondence:m.
moosaei@basu.
ac.
irDepartmentofMathematics,Bu-AliSinaUniversity,Hamedan,IranAbstractThepresentstudyfocusesonprovingtheexistenceofcoincidencepointsforself-mappingssatisfyingageneralizedcontractiveconditionwithintheframeworkofconvexmetricspaces.
Theexistenceofcommonxedpointsforweaklycompatibleself-mappingsaswellasBanachoperatorpairsundercertaingeneralizedcontractionsinaconvexmetricspaceisalsoestablished.
MSC:47H09;47H10;47H19;54H25Keywords:Banachoperatorpairs;coincidencepoints;commonxedpoints;compatiblemappings;convexmetricspaces;xedpoints;weaklycompatiblepair1IntroductionandpreliminariesIn,Takahashi[]introducedthenotionofconvexityinmetricspacesandprovedthatallnormedspacesandtheirconvexsubsetsareconvexmetricspaces.
Healsogavesomeexamplesoftheconvexmetricspaceswhicharenotembeddedinanynormed/Banachspaces.
AfterwardGuay,SinghandWhittield[],BegandAzam[],Beg,Azam,AliandMinhas[],ShimizuandTakahashi[],Ciric[],Beg[,],BegandAbbas[],andmanyotherauthorshavestudiedxedpointtheoremsinconvexmetricspaces.
Inthispaper,weintroduce(α,β,γ,η)-generalizedcontractionpairsandstudytheexis-tenceofacoincidencepointforsuchpairsinaconvexmetricspaceundercertaincondi-tions(seeTheorem.
).
Consequently,weprovetheexistenceofacommonxedpointforweaklycompatiblemappingsandalsoBanachoperatorpairswhichare(α,β,γ,η)-generalizedcontractionpairs(seeTheorem.
andTheorem.
).
Wenowreviewnotationsanddenitionsneeded.
WedenotebyNandRthesetofnaturalnumbersandthesetofrealnumbers,respectively.
WealsodenotebyItheidentitymapping.
Inwhatfollows,(X,d)isametricspace,andCisanonemptysubsetofX.
Denition.
LetSandTbetwoself-mappingsofC.
ApointxofCiscalled(i)axedpointofTifTx=x,(ii)acommonxedpointofthepair(S,T)ifSx=Tx=x,and(iii)acoincidencepointofthepair(S,T)ifSx=Tx.
ThesetofxedpointsofTisdenotedbyF(T).
Thesetofcommonxedpoints(respec-tively,coincidencepoints)ofthepair(S,T)isdenotedbyF(S,T)(respectively,C(S,T)).
NotethatC(I,T)=F(T).
Denition.
LetSandTbetwoself-mappingsofC.
ThemappingTiscalled2014Moosaei;licenseeSpringer.
ThisisanOpenAccessarticledistributedunderthetermsoftheCreativeCommonsAttribu-tionLicense(http://creativecommons.
org/licenses/by/2.
0),whichpermitsunrestricteduse,distribution,andreproductioninanymedium,providedtheoriginalworkisproperlycited.
MoosaeiFixedPointTheoryandApplications2014,2014:98Page2of8http://www.
fixedpointtheoryandapplications.
com/content/2014/1/98(i)acontractionifthereexistsk∈[,)suchthatd(Tx,Ty)≤kd(x,y)forallx,y∈C,(ii)anS-contractionifthereexistsk∈[,)suchthatd(Tx,Ty)≤kd(Sx,Sy)forallx,y∈C,(iii)nonexpansiveifd(Tx,Ty)≤d(x,y)forallx,y∈C,and(iv)S-nonexpansiveifd(Tx,Ty)≤d(Sx,Sy)forallx,y∈C.
Denition.
LetSandTbetwoself-mappingsofC.
Thepair(S,T)issaidtobe(i)commutingifSTx=TSxforallx∈C,(ii)R-weaklycommuting[]ifthereexistsR>suchthatd(STx,TSx)≤Rd(Sx,Tx)forallx∈C.
IfR=,thenthemappingsarecalledweaklycommuting[],(iii)compatible[]iflimn→∞d(STxn,TSxn)=,whenever{xn}∞n=isasequenceinCsuchthatlimn→∞Sxn=limn→∞Txn=xforsomex∈C,and(iv)weaklycompatibleiftheycommuteonC(S,T)i.
e.
STx=TSxforallx∈C(S,T)(see[,]formoredetails).
Itiswellknownthatcommutingmappingsareweaklycommuting,andweaklycommut-ingmappingsareR-weaklymappings.
Moreover,R-weaklymappingsarecompatible,andcompatiblemappingsareweaklycompatible.
Thefollowingexampleshowsthattheconversesoftheaboveresultsarenottrueingeneral.
Example.
LetX=Rwiththeusualmetricd(x,y)=|x–y|forallx,y∈X,wehave:()LetC=[,].
LetSx=xandTx=xforallx∈C.
ItistrivialthatSandTareweaklycommutingbutarenotcommuting.
()LetC=[,∞].
ConsiderSx=x–andTx=xforallx∈C.
ThenSandTare-weaklycommutingbutarenotweaklycommuting(see[]).
()LetC=X,Sx=x,Tx=x,x∈C.
ThenSandTarecompatiblebutarenotR-weaklycommuting(see[,,]formoredetails).
()LetC=[,],anddeneself-mappingsSandTofCbyS()=,S(x)=iforηorη,thenηorηorη<α+γholds.
CompetinginterestsTheauthordeclaresthattheyhavenocompetinginterests.
AcknowledgementsTheauthorisgratefultothereviewersfortheirvaluablecommentswhichimprovedthecontentsofthemanuscript.
Received:28November2013Accepted:27March2014Published:16Apr2014MoosaeiFixedPointTheoryandApplications2014,2014:98Page8of8http://www.
fixedpointtheoryandapplications.
com/content/2014/1/98References1.
Takahashi,T:AconvexityinmetricspacesandnonexpansivemappingI.
KodaiMath.
Semin.
Rep.
22,142-149(1970)2.
Guay,MD,Singh,KL,Whiteld,JHM:Fixedpointtheoremsfornonexpansivemappingsinconvexmetricspaces.
In:ProceedingsofConferenceonNonlinearAnalysis.
LectureNotesinPureandAppliedMathematics,vol.
80,pp.
179-189.
Dekker,NewYork(1982)3.
Beg,I,Azam,A:Fixedpointonstar-shapedsubsetsofconvexmetricspaces.
IndianJ.
PureAppl.
Math.
18,594-596(1987)4.
Beg,I,Azam,A,Ali,F,Minhas,T:Somexedpointtheoremsinconvexmetricspaces.
Rend.
Circ.
Mat.
PalermoXL,307-315(1991)5.
Shimizu,T,Takahashi,W:Fixedpointtheoremsincertainconvexmetricspaces.
Math.
Jpn.
37,855-859(1992)6.
Ciric,L:Onsomediscontinuousxedpointtheoremsinconvexmetricspaces.
Czechoslov.
Math.
J.
43(188),319-326(1993)7.
Beg,I:Structureofthesetofxedpointsofnonexpansivemappingsonconvexmetricspaces.
Ann.
Univ.
MariaeCurie-Skodowska,Sect.
ALII,7-14(1998)8.
Beg,I:Inequalitiesinmetricspaceswithapplications.
Topol.
MethodsNonlinearAnal.
17,183-190(2001)9.
Beg,I,Abbas,M:FixedpointsandbestapproximationinMengerconvexmetricspaces.
Arch.
Math.
41,389-397(2005)10.
Pant,RP:Commonxedpointsofnoncommutingmappings.
J.
Math.
Anal.
Appl.
188,436-440(1994)11.
Sessa,S:Onaweakcommutativityconditionofmappingsinxedpointconsiderations.
Publ.
Inst.
Math.
32,149-153(1982)12.
Jungck,G:Compatiblemappingsandcommonxedpoints.
Int.
J.
Math.
Math.
Sci.
9,771-779(1986)13.
Jungck,G,Rhoades,BE:Fixedpointforsetvaluedfunctionswithoutcontinuity.
IndianJ.
PureAppl.
Math.
29(3),227-238(1998)14.
Chugh,R,Kumar,S:Commonxedpointsforweaklycompatiblemaps.
Proc.
IndianAcad.
Sci.
Math.
Sci.
111,241-247(2001)15.
Jungck,G:Commonxedpointsforcommutingandcompatiblemapsoncompacta.
Proc.
Am.
Math.
Soc.
103,978-983(1988)16.
Jungck,G:CommonxedpointtheoremsforcompatibleselfmapsofHausdortopologicalspaces.
FixedPointTheoryAppl.
3,355-363(2005)17.
Chen,J,Li,Z:Commonxed-pointsforBanachoperatorpairsinbestapproximation.
J.
Math.
Anal.
Appl.
336,1466-1475(2007)18.
Hussain,N:CommonxedpointsinbestapproximationforBanachoperatorpairswithCirictypeI-contractions.
J.
Math.
Anal.
Appl.
338,1351-1363(2008)19.
Agarwal,RP,O'Regan,D,Sahu,DR:FixedPointTheoryforLipschitzian-TypeMappingswithApplications.
Springer,Heidelberg(2009)20.
Hussain,N,Abbas,M,Kim,JK:CommonxedpointandinvariantapproximationinMengerconvexmetricspaces.
Bull.
KoreanMath.
Soc.
48,671-680(2008)21.
Moosaei,M:Fixedpointtheoremsinconvexmetricspaces.
FixedPointTheoryAppl.
2012,ArticleID164(2012).
doi:10.
1186/1687-1812-2012-16410.
1186/1687-1812-2014-98Citethisarticleas:Moosaei:Commonxedpointsforsomegeneralizedcontractionpairsinconvexmetricspaces.
FixedPointTheoryandApplications2014,2014:98
fixedpointtheoryandapplications.
com/content/2014/1/98RESEARCHOpenAccessCommonxedpointsforsomegeneralizedcontractionpairsinconvexmetricspacesMohammadMoosaei**Correspondence:m.
moosaei@basu.
ac.
irDepartmentofMathematics,Bu-AliSinaUniversity,Hamedan,IranAbstractThepresentstudyfocusesonprovingtheexistenceofcoincidencepointsforself-mappingssatisfyingageneralizedcontractiveconditionwithintheframeworkofconvexmetricspaces.
Theexistenceofcommonxedpointsforweaklycompatibleself-mappingsaswellasBanachoperatorpairsundercertaingeneralizedcontractionsinaconvexmetricspaceisalsoestablished.
MSC:47H09;47H10;47H19;54H25Keywords:Banachoperatorpairs;coincidencepoints;commonxedpoints;compatiblemappings;convexmetricspaces;xedpoints;weaklycompatiblepair1IntroductionandpreliminariesIn,Takahashi[]introducedthenotionofconvexityinmetricspacesandprovedthatallnormedspacesandtheirconvexsubsetsareconvexmetricspaces.
Healsogavesomeexamplesoftheconvexmetricspaceswhicharenotembeddedinanynormed/Banachspaces.
AfterwardGuay,SinghandWhittield[],BegandAzam[],Beg,Azam,AliandMinhas[],ShimizuandTakahashi[],Ciric[],Beg[,],BegandAbbas[],andmanyotherauthorshavestudiedxedpointtheoremsinconvexmetricspaces.
Inthispaper,weintroduce(α,β,γ,η)-generalizedcontractionpairsandstudytheexis-tenceofacoincidencepointforsuchpairsinaconvexmetricspaceundercertaincondi-tions(seeTheorem.
).
Consequently,weprovetheexistenceofacommonxedpointforweaklycompatiblemappingsandalsoBanachoperatorpairswhichare(α,β,γ,η)-generalizedcontractionpairs(seeTheorem.
andTheorem.
).
Wenowreviewnotationsanddenitionsneeded.
WedenotebyNandRthesetofnaturalnumbersandthesetofrealnumbers,respectively.
WealsodenotebyItheidentitymapping.
Inwhatfollows,(X,d)isametricspace,andCisanonemptysubsetofX.
Denition.
LetSandTbetwoself-mappingsofC.
ApointxofCiscalled(i)axedpointofTifTx=x,(ii)acommonxedpointofthepair(S,T)ifSx=Tx=x,and(iii)acoincidencepointofthepair(S,T)ifSx=Tx.
ThesetofxedpointsofTisdenotedbyF(T).
Thesetofcommonxedpoints(respec-tively,coincidencepoints)ofthepair(S,T)isdenotedbyF(S,T)(respectively,C(S,T)).
NotethatC(I,T)=F(T).
Denition.
LetSandTbetwoself-mappingsofC.
ThemappingTiscalled2014Moosaei;licenseeSpringer.
ThisisanOpenAccessarticledistributedunderthetermsoftheCreativeCommonsAttribu-tionLicense(http://creativecommons.
org/licenses/by/2.
0),whichpermitsunrestricteduse,distribution,andreproductioninanymedium,providedtheoriginalworkisproperlycited.
MoosaeiFixedPointTheoryandApplications2014,2014:98Page2of8http://www.
fixedpointtheoryandapplications.
com/content/2014/1/98(i)acontractionifthereexistsk∈[,)suchthatd(Tx,Ty)≤kd(x,y)forallx,y∈C,(ii)anS-contractionifthereexistsk∈[,)suchthatd(Tx,Ty)≤kd(Sx,Sy)forallx,y∈C,(iii)nonexpansiveifd(Tx,Ty)≤d(x,y)forallx,y∈C,and(iv)S-nonexpansiveifd(Tx,Ty)≤d(Sx,Sy)forallx,y∈C.
Denition.
LetSandTbetwoself-mappingsofC.
Thepair(S,T)issaidtobe(i)commutingifSTx=TSxforallx∈C,(ii)R-weaklycommuting[]ifthereexistsR>suchthatd(STx,TSx)≤Rd(Sx,Tx)forallx∈C.
IfR=,thenthemappingsarecalledweaklycommuting[],(iii)compatible[]iflimn→∞d(STxn,TSxn)=,whenever{xn}∞n=isasequenceinCsuchthatlimn→∞Sxn=limn→∞Txn=xforsomex∈C,and(iv)weaklycompatibleiftheycommuteonC(S,T)i.
e.
STx=TSxforallx∈C(S,T)(see[,]formoredetails).
Itiswellknownthatcommutingmappingsareweaklycommuting,andweaklycommut-ingmappingsareR-weaklymappings.
Moreover,R-weaklymappingsarecompatible,andcompatiblemappingsareweaklycompatible.
Thefollowingexampleshowsthattheconversesoftheaboveresultsarenottrueingeneral.
Example.
LetX=Rwiththeusualmetricd(x,y)=|x–y|forallx,y∈X,wehave:()LetC=[,].
LetSx=xandTx=xforallx∈C.
ItistrivialthatSandTareweaklycommutingbutarenotcommuting.
()LetC=[,∞].
ConsiderSx=x–andTx=xforallx∈C.
ThenSandTare-weaklycommutingbutarenotweaklycommuting(see[]).
()LetC=X,Sx=x,Tx=x,x∈C.
ThenSandTarecompatiblebutarenotR-weaklycommuting(see[,,]formoredetails).
()LetC=[,],anddeneself-mappingsSandTofCbyS()=,S(x)=iforηorη,thenηorηorη<α+γholds.
CompetinginterestsTheauthordeclaresthattheyhavenocompetinginterests.
AcknowledgementsTheauthorisgratefultothereviewersfortheirvaluablecommentswhichimprovedthecontentsofthemanuscript.
Received:28November2013Accepted:27March2014Published:16Apr2014MoosaeiFixedPointTheoryandApplications2014,2014:98Page8of8http://www.
fixedpointtheoryandapplications.
com/content/2014/1/98References1.
Takahashi,T:AconvexityinmetricspacesandnonexpansivemappingI.
KodaiMath.
Semin.
Rep.
22,142-149(1970)2.
Guay,MD,Singh,KL,Whiteld,JHM:Fixedpointtheoremsfornonexpansivemappingsinconvexmetricspaces.
In:ProceedingsofConferenceonNonlinearAnalysis.
LectureNotesinPureandAppliedMathematics,vol.
80,pp.
179-189.
Dekker,NewYork(1982)3.
Beg,I,Azam,A:Fixedpointonstar-shapedsubsetsofconvexmetricspaces.
IndianJ.
PureAppl.
Math.
18,594-596(1987)4.
Beg,I,Azam,A,Ali,F,Minhas,T:Somexedpointtheoremsinconvexmetricspaces.
Rend.
Circ.
Mat.
PalermoXL,307-315(1991)5.
Shimizu,T,Takahashi,W:Fixedpointtheoremsincertainconvexmetricspaces.
Math.
Jpn.
37,855-859(1992)6.
Ciric,L:Onsomediscontinuousxedpointtheoremsinconvexmetricspaces.
Czechoslov.
Math.
J.
43(188),319-326(1993)7.
Beg,I:Structureofthesetofxedpointsofnonexpansivemappingsonconvexmetricspaces.
Ann.
Univ.
MariaeCurie-Skodowska,Sect.
ALII,7-14(1998)8.
Beg,I:Inequalitiesinmetricspaceswithapplications.
Topol.
MethodsNonlinearAnal.
17,183-190(2001)9.
Beg,I,Abbas,M:FixedpointsandbestapproximationinMengerconvexmetricspaces.
Arch.
Math.
41,389-397(2005)10.
Pant,RP:Commonxedpointsofnoncommutingmappings.
J.
Math.
Anal.
Appl.
188,436-440(1994)11.
Sessa,S:Onaweakcommutativityconditionofmappingsinxedpointconsiderations.
Publ.
Inst.
Math.
32,149-153(1982)12.
Jungck,G:Compatiblemappingsandcommonxedpoints.
Int.
J.
Math.
Math.
Sci.
9,771-779(1986)13.
Jungck,G,Rhoades,BE:Fixedpointforsetvaluedfunctionswithoutcontinuity.
IndianJ.
PureAppl.
Math.
29(3),227-238(1998)14.
Chugh,R,Kumar,S:Commonxedpointsforweaklycompatiblemaps.
Proc.
IndianAcad.
Sci.
Math.
Sci.
111,241-247(2001)15.
Jungck,G:Commonxedpointsforcommutingandcompatiblemapsoncompacta.
Proc.
Am.
Math.
Soc.
103,978-983(1988)16.
Jungck,G:CommonxedpointtheoremsforcompatibleselfmapsofHausdortopologicalspaces.
FixedPointTheoryAppl.
3,355-363(2005)17.
Chen,J,Li,Z:Commonxed-pointsforBanachoperatorpairsinbestapproximation.
J.
Math.
Anal.
Appl.
336,1466-1475(2007)18.
Hussain,N:CommonxedpointsinbestapproximationforBanachoperatorpairswithCirictypeI-contractions.
J.
Math.
Anal.
Appl.
338,1351-1363(2008)19.
Agarwal,RP,O'Regan,D,Sahu,DR:FixedPointTheoryforLipschitzian-TypeMappingswithApplications.
Springer,Heidelberg(2009)20.
Hussain,N,Abbas,M,Kim,JK:CommonxedpointandinvariantapproximationinMengerconvexmetricspaces.
Bull.
KoreanMath.
Soc.
48,671-680(2008)21.
Moosaei,M:Fixedpointtheoremsinconvexmetricspaces.
FixedPointTheoryAppl.
2012,ArticleID164(2012).
doi:10.
1186/1687-1812-2012-16410.
1186/1687-1812-2014-98Citethisarticleas:Moosaei:Commonxedpointsforsomegeneralizedcontractionpairsinconvexmetricspaces.
FixedPointTheoryandApplications2014,2014:98
RangCloud19.8元/月,香港cn2云主机,美国西雅图高防云主机28元/月起
rangcloud怎么样?rangcloud是去年年初开办的国人商家,RangCloud是一家以销售NAT起步,后续逐渐开始拓展到VPS及云主机业务,目前有中国香港、美国西雅图、韩国NAT、广州移动、江门移动、镇江BGP、山东联通、山东BGP等机房。目前,RangCloud提供香港CN2线路云服务器,电信走CN2、联通移动直连,云主机采用PCle固态硬盘,19.8元/月起,支持建站使用;美国高防云...

无忧云(25元/月),国内BGP高防云服务器 2核2G5M
无忧云官网无忧云怎么样 无忧云服务器好不好 无忧云值不值得购买 无忧云,无忧云是一家成立于2017年的老牌商家旗下的服务器销售品牌,现由深圳市云上无忧网络科技有限公司运营,是正规持证IDC/ISP/IRCS商家,主要销售国内、中国香港、国外服务器产品,线路有腾讯云国外线路、自营香港CN2线路等,都是中国大陆直连线路,非常适合免北岸建站业务需求和各种负载较高的项目,同时国内服务器也有多个BGP以及高...

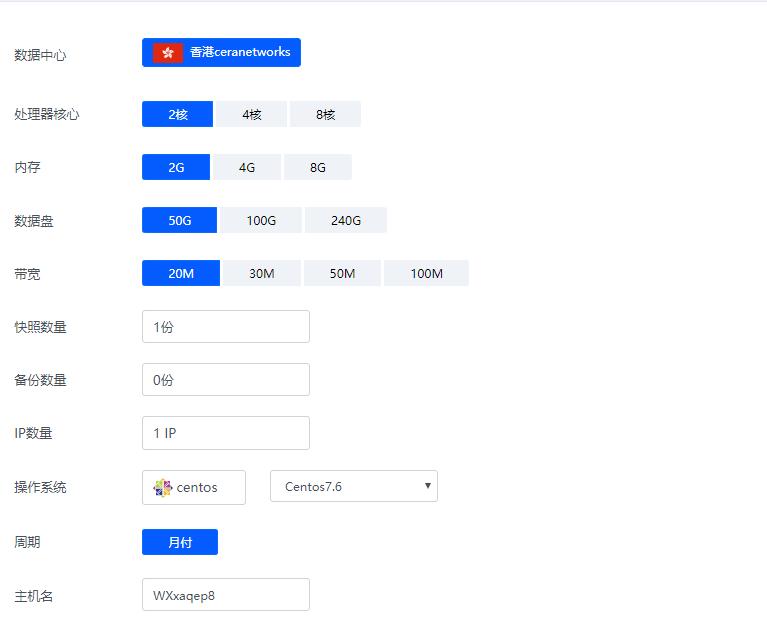
香港ceranetworks(69元/月) 2核2G 50G硬盘 20M 50M 100M 不限流量
香港ceranetworks提速啦是成立于2012年的十分老牌的一个商家这次给大家评测的是 香港ceranetworks 8核16G 100M 这款产品 提速啦老板真的是豪气每次都给高配我测试 不像别的商家每次就给1核1G,废话不多说开始跑脚本。香港ceranetworks 2核2G 50G硬盘20M 69元/月30M 99元/月50M 219元/月100M 519元/月香港ceranetwork...
98成人网为你推荐
-
areaiphone支持ipadsetOwnerjava湖北省网易yeah支付宝调整还款日花呗还款日是什么时候呢支付宝注册网站在哪里注册支付宝资费标准中国移动38元套餐介绍开放平台众安开放平台是干什么的?上面的众推广是什么?中国保健养猪网最具权威的养猪信息网站是哪个 啊申请400电话400电话如何申请办理?