事件统计概率知识点梳理总结
统计概率知识点梳理总结
第一章 随机事件与概率
一、教学要求
1 理解随机事件的概念了解随机试验、样本空间的概念掌握事件之间的关系与运算
2 了解概率的各种定义掌握概率的基本性质并能运用这些性质进行概率计算
3 理解条件概率的概念掌握概率的乘法公式、全概率公式、 贝叶斯公式并能运用这些公式进行概率计算
4 理解事件的独立性概念掌握运用事件独立性进行概率计算
5 掌握贝努里概型及其计算能够将实际问题归结为贝努里概型然后用二项概率计算有关事件的概率
本章重点随机事件的概率计算
二、知识要点
1 随机试验与样本空间
具有下列三个特性的试验称为随机试验
(1)试验可以在相同的条件下重复地进行 ·
(2)每次试验的可能结果不止一个但事先知道每次试验所有可能的结果
(3)每次试验前不能确定哪一个结果会出现
试验的所有可能结果所组成的集合为样本空间用 表示其中的每一个结果用表示 称为样本空间中的样本点记作
2 随机事件
在随机试验中把一次试验中可能发生也可能不发生、而在大量重复试验中却呈现某种规律性的事情称为随机事件(简称事件) 通常把必然事件(记作 )与不可能事件(记作 )
看作特殊的随机事件
3 **事件的关系及运算
(1)包含若事件 发生一定导致事件 发生那么称事件 包含事件 记作 (或 )
(2)相等若两事件 与 相互包含即 且 那么称事件 与相等记作
(3)和事件 “事件A与事件B中至少有一个发生”这一事件称为A与B的和事件记作 “n个事件 中至少有一事件发生”这一事件称为
的和记作 简记为
(4)积事件 “事件A与事件B同时发生”这一事件称为A与B的积事件记作(简记为 ) “n个事件 同时发生”这一事件称为
的积事件记作 简记为 或 )
(5)互不相容若事件A和B不能同时发生即 那么称事件A与B互不相容(或互斥) 若n个事件 中任意两个事件不能同时发生即
(1≤i<j≤几) 那么称事件 互不相容
(6)对立事件若事件A和B互不相容、且它们中必有一事件发生即 且
那么称A与B是对立的事件A的对立事件(或逆事件)记作
(7)差事件若事件A发生且事件B不发生那么称这个事件为事件A与B的差事件记作 (或 )
(8)交换律对任意两个事件和B有
(9)结合律对任意事件ABC有
(10)分配律对任意事件ABC有
(11)德摩根De Morgan法则对任意事件A和B有
, .
4 频率与概率的定义
(1)频率的定义
设随机事件A在n次重复试验中发生了 次则比值 n称为随机事件A发生的频率记作 即 .
(2)概率的统计定义
在进行大量重复试验中随机事件A发生的频率具有稳定性即当试验次数n很大时频率 在一个稳定的值 (0< <1)附近摆动规定事件A发生的频率的稳定值 为概率即
(3) **古典概率的定义
具有下列两个特征的随机试验的数学模型称为古典概型
(i) 试验的样本空间 是个有限集不妨记作 ;
(ii) 在每次试验中每个样本点 ( 出现的概率相同即
在古典概型中规定事件A的概率为
(4) 几何概率的定义
如果随机试验的样本空间是一个区域(可以是直线上的区间、平面或空间中的区域) 且样本空间中每个试验结果的出现具有等可能性那么规定事件的概率为
·
(5) 概率的公理化定义
设随机试验的样本空间为 随机事件A是 的子集 是实值函数若满足下列三条公理
公理1 (非负性) 对于任一随机事件有 ≥0
公理2 (规范性) 对于必然事件 有
公理3 (可列可加性) 对于两两互不相容的事件 有
则称 为随机事件的概率
5 **概率的性质
由概率的三条公理可导出下面概率的一些重要性质
(1)
(2) (有限可加性)设n个事件 两两互不相容则有
(3)对于任意一个事件A
(4)若事件AB满足 则有
,
(5)对于任意一个事件A有
(6) (加法公式)对于任意两个事件AB有
.
对于任意n个事件 有
.
6 **条件概率与乘法公式
设A与B是两个事件在事件B发生的条件下事件A发生的概率称为条件概率记作当 规定
.
在同一条件下条件概率具有概率的一切性质
乘法公式对于任意两个事件A与B当 , 时有
.
7 *随机事件的相互独立性
如果事件A与B满足
那么称事件A与B相互独立
关于事件A月的独立性有下列两条性质
- 事件统计概率知识点梳理总结相关文档
- 北京大学生雅虎公司实习报告内容完整word文档
- 中位数2014年全国各地中考数学真题分类解析汇编:14 统计
- 信息化2014软件产业统计制度
- 雅虎雅虎为什么输在企业文化(企业文化范文)
- 词典babylon、有道桌面词典、雅虎乐译和灵格斯
- 企业电大企业统计形成性考核册(最新完整版小抄)-2013中央电大专科《企业统计》考试小抄
atcloud:480G超高防御VPS低至$4/月,美国/新加坡等6机房,512m内存/1核/500g硬盘/不限流量
atcloud主要提供常规cloud(VPS)和storage(大硬盘存储)系列VPS,其数据中心分布在美国(俄勒冈、弗吉尼亚)、加拿大、英国、法国、德国、新加坡,所有VPS默认提供480Gbps的超高DDoS防御+不限流量,杜绝DDoS攻击骚扰,比较适合海外建站等相关业务。ATCLOUD.NET是一家成立于2020年的海外主机商,主要提供KVM架构的VPS产品、LXC容器化产品、权威DNS智能解...
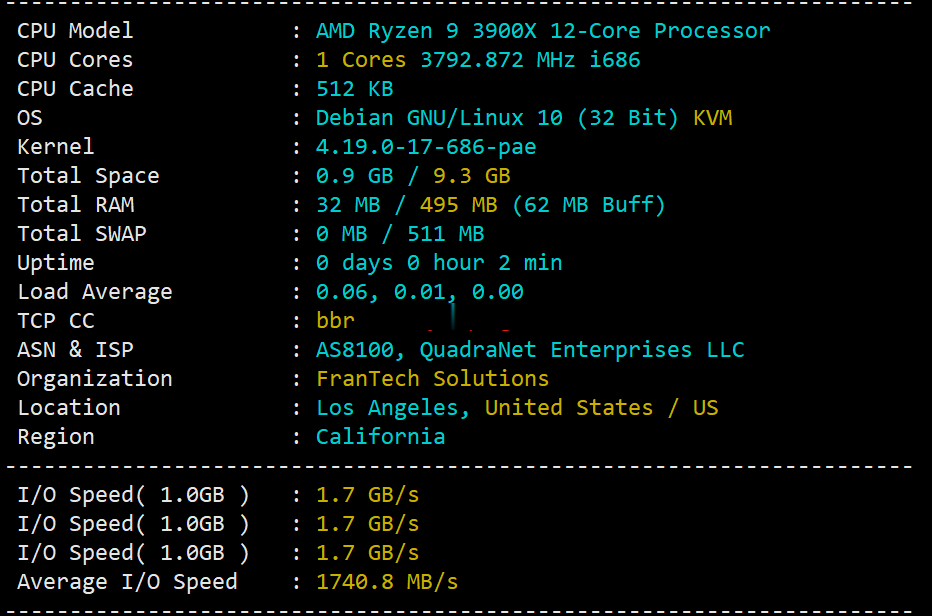
buyvm迈阿密机房VPS国内首发测评,高性能平台:AMD Ryzen 9 3900x+DDR4+NVMe+1Gbps带宽不限流量
buyvm的第四个数据中心上线了,位于美国东南沿海的迈阿密市。迈阿密的VPS依旧和buyvm其他机房的一样,KVM虚拟,Ryzen 9 3900x、DDR4、NVMe、1Gbps带宽、不限流量。目前还没有看见buyvm上架迈阿密的block storage,估计不久也会有的。 官方网站:https://my.frantech.ca/cart.php?gid=48 加密货币、信用卡、PayPal、...
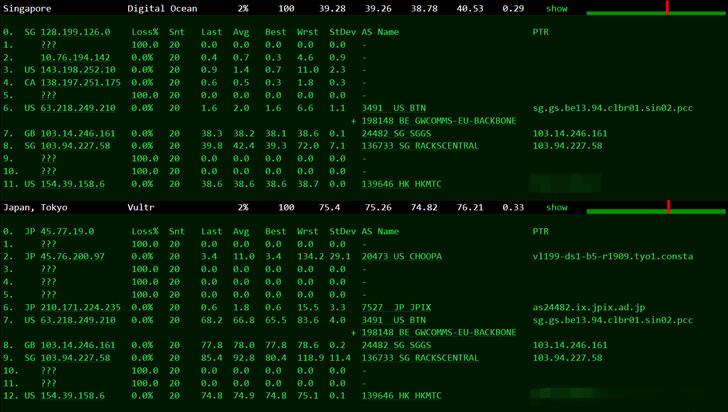
Megalayer新加坡服务器国际带宽线路测评
前几天有关注到Megalayer云服务器提供商有打算在月底的时候新增新加坡机房,这个是继美国、中国香港、菲律宾之外的第四个机房。也有工单询问到官方,新加坡机房有包括CN2国内优化线路和国际带宽,CN2优化线路应该是和菲律宾差不多的。如果我们追求速度和稳定性的中文业务,建议还是选择CN2优化带宽的香港服务器。这里有要到Megalayer新加坡服务器国际带宽的测试服务器,E3-1230配置20M国际带...
-
杀毒软件哪个好什么杀毒软件比较好呢??电脑管家和360哪个好腾讯电脑管家和360安全卫士哪个更好江门旅游景点哪个好玩的地方江门有那个地方好玩呢宝来和朗逸哪个好宝来和朗逸哪个好ps软件哪个好PS软件用哪种比较好?急用!等额本息等额本金哪个好房贷是等额本金划算还是等额本息划算尼康和佳能单反哪个好入门的单反相机 佳能和尼康哪个好?海克斯皮肤哪个好lol100块抽11次的海克斯宝箱值得买吗网络机顶盒哪个好什么牌子的网络机顶盒最好牡丹江教育云空间登录云端学习如何登录?