函数什么是函数
什么叫做函数?
补充 functions 数学中的一种对应关系,是从非空集合A到实数集B的对应。简单地说,甲随着乙变,甲就是乙的函数 。
精确地说,设X是一个非空集合,Y是非空数集 ,f是个对应法则 , 若对X中的每个x,按对应法则f,使Y中存在唯一的一个元素y与之对应 , 就称对应法则f是X上的一个函数,记作y=f(x),称X为函数f(x)的定义域,集合{y|y=f(x),x∈X}为其值域(值域是Y的子集),x叫做自变量,y叫做因变量,习惯上也说y是x的函数。
若先定义映射的概念,可以简单定义函数为:定义在非空数集之间的映射称为函数。
例1:y=sinx X=[0,2π],Y=[-1,1] ,它给出了一个函数关系。
当然 ,把Y改为Y1=(a,b) ,a<b为任意实数,仍然是一个函数关系。
其深度y与一岸边点 O到测量点的距离 x 之间的对应关系呈曲线,这代表一个函数,定义域为[0,b]。
以上3例展示了函数的三种表示法:公式法 , 表格法和图像法。
复合函数 有3个变量,y是u的函数,y=ψ(u),u是x的函数,u=f(x),往往能形成链:y通过中间变量u构成了x的函数: x→u→y,这要看定义域:设ψ的定义域为U 。
f的值域为U,当U*ÍU时,称f与ψ 构成一个复合函数 , 例如 y=lgsinx,x∈(0,π)。
此时sinx>0 ,lgsinx有意义 。
但如若规定x∈(-π,0),此时sinx<0 ,lgsinx无意义 ,就成不了复合函数。
反函数 就关系而言,一般是双向的 ,函数也如此 ,设y=f(x)为已知的函数,若对每个y∈Y,有唯一的x∈X,使f(x)=y,这是一个由y找x的过程 ,即x成了y的函数 ,记为x=f -1(y)。
称f -1为f的反函数。
习惯上用x表示自变量 ,故这个函数仍记为y=f -1(x) ,例如 y=sinx与y=arcsinx 互为反函数。
在同一坐标系中,y=f(x)与y=f -1(x)的图形关于直线y=x对称。
隐函数 若能由函数方程 F(x,y)=0 确定y为x的函数y=f(x),即F(x,f(x))≡0,就称y是x的隐函数。
思考:隐函数是否为函数?因为在其变化的过程中并不满足“一对一”和“多对一”
函数是什么?有什么函数?
定义 传统 在某一变化过程中有两个变量x和y,对于x的每一个确定的值,y都有唯一确定的值与它对应,则y与x有函数关系。一般用 表示。
其中x叫做自变量,y叫做因变量。
经典 在某个坐标变化过程中,如果有两个变量x和y,对每一个给定的x值,y都有唯一确定的值与它对应,确定y=x的函数。
x=自变量,y作为x的因变量。
另外,若对于每一个给定的y值,都有X与其对应。
函数是英文单词function的翻译,做这个翻译的最早是中国清朝数学家李善兰,出现于其著作《代数学》。
之所以这么翻译,他给出的原因是“凡此变数中函彼变数者,则此为彼之函数”,也即函数指一个量随着另一个量的变化而变化,或者说一个量中含有另一个量。
此后这个名称一直沿用。
当然这和现代数学用集合定义的函数有一定区别。
function这个单词也更多用于表达“功能”“起作用”的意思。
现代 一般地,给定非空数集A,B,按照某个对应法则f,使得A中任一元素x,都有B中唯一确定的y与之对应,那么从集合A到集合B的这个对应,叫做从集合A到集合B的一个函数。
记作:x→y=f(x),x∈A.集合A叫做函数的定义域,记为D,集合{y∣y=f(x),x∈A}叫做值域,记为C。
定义域,值域,对应法则称为函数的三要素。
一般书写为y=f(x),x∈D.若省略定义域,则指使函数有意义的集合。
一次函数 二次函数 三角函数 幂函数 指数函数 复变函数 程序函数 复合函数 Word函数 好多分支哦哦 好评哦哦
什么是函数
就是完成程序某一功能的模块。
每个模块都有自己的功能且可以互相调用(主函数可以调用其它函数但是其它函数不能调用主函数(main函数))
例如
#include<stdio.h> #define N 5 void f(int *p)---------------------------------->被命名为F的函数 被调用后运行自己的功能
{int s=0,i; for(i=0;i<N;i++) if(i%2) s+=*(p+i); printf("%d",s); } main()------------------------------------------------->主函数 用语调用 {int a[N]={3,2,7,9,4},*p=a; f(p); printf(" "); }
BuyVM商家4个机房的官方测试IP地址和测速文件
BuyVM 商家算是有一些年头,从早年提供低价便宜VPS主机深受广大网友抢购且也遭到吐槽的是因为审核账户太过于严格。毕竟我们国内的个人注册账户喜欢账户资料乱写,毕竟我们看英文信息有些还是比较难以识别的,于是就注册信息的时候随便打一些字符,这些是不能通过的。前几天,我们可以看到BUYVM商家有新增加迈阿密机房,而且商家有提供大硬盘且不限制流量的VPS主机,深受有一些网友的喜欢。目前,BUYVM商家有...
Hostiger发布哥伦布日提供VPS主机首月七折优惠 月费2.79美元
Hostiger商家我们可能以前也是有见过的,以前他们的域名是Hostigger,后来进行微调后包装成现在的。而且推出Columbus Day哥伦布日优惠活动,提供全场的VPS主机首月7折月付2.79美元起的优惠。这里我们普及一下基础知识,Columbus Day ,即为每年10月12日,是一些美洲国家的节日,纪念克里斯托弗·哥伦布在北美登陆,为美国的联邦假日。Hostiger 商家是一个成立于2...
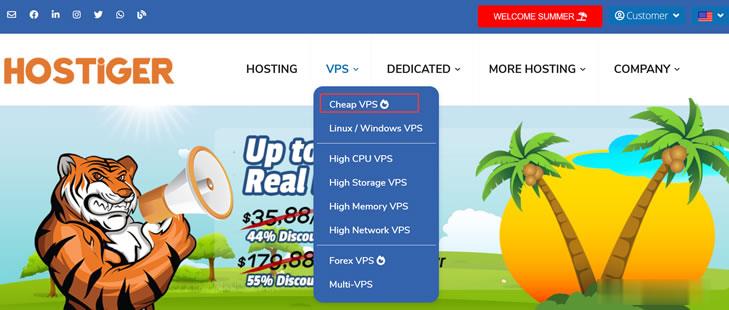
阿里云香港 16核32G 20M 999元/月
阿里云香港配置图提速啦是成立于2012年的十分老牌的一个商家这次给大家评测的是 阿里云香港 16核32G 20M 这款产品,单单说价格上就是十分的离谱原价8631元/月的现价只要 999元 而且还有个8折循环优惠。废话不多说直接进入正题。优惠时间 2021年8月20日-2021年9月20日 优惠码 wn789 8折优惠阿里云香港BGP专线 16核32G 10M带宽 优惠购买 399元购买链接阿里云...
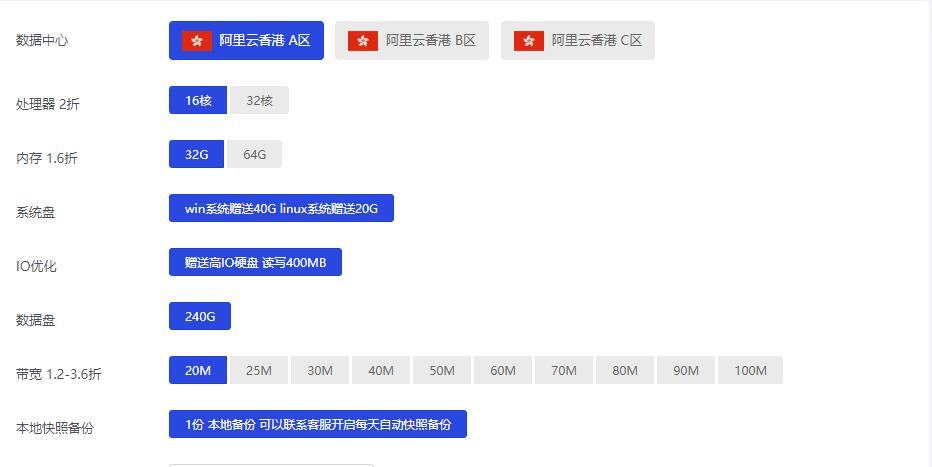
-
销售报表销售日报表做法?好享购物我国省级电视台有哪些表单控件web表单控件类型有哪些显示系统电脑开机显示各种系统选项是什么回事价格咨询心理咨询价格昂贵吗无线存储无线摄像头里的远程存储和本地存储是怎么回事?网通玩电信游戏卡怎么办我的网是网通,我玩电信区的游戏,总是卡,怎么办呢等保测评机构等保测评机构,时代新威怎么样?阿里学院首页在阿里学院必须实名认证吗什么是3g什么是3G网络?