拓扑排序拓扑排序时间复杂度o(n+e)怎么算的?
拓扑排序 时间:2021-08-09 阅读:()
拓扑排序和关键路径是如何实现的
拓扑排序的实现步骤: 由AOV网构造拓扑序列的拓扑排序算法主要是循环执行以下三步,直到不存在入度为0的顶点为止; (1) 选择一个入度为0的顶点并输出之; (2) 从网中删除此顶点及所有出边; (3) 循环结束后,若输出的顶点数小于网中的顶点数,则输出“有回路”信息,否则输出的顶点序列就是一种拓扑序列。求关键路径的算法: (1) 输入e条弧<j,k>,建立AOE网的存储结构。
(2) 从源点v1出发,令ve(1)=0,求 ve(j) 2<=j<=n。
(3) 从汇点vn出发,令vl(n)=ve(n),求 vl(i) 1<=i<=n-1。
(4) 根据各顶点的ve和vl值,求每条弧s(活动)的最早开始时间e(s)和最晚开始时间l(s),其中e(s)=l(s)的为关键活动。
数据结构问题~什么图可以进行拓扑排序~什么图不能进行拓扑排序?
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若拓扑排序(Topological Sort) 什么是拓扑序列 通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。
简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
离散数学中关于偏序和全序的定义: 若集合X上的关系是R是自反的、反对称的和传递的,则称R是集合X上的偏序关系。
设R是集合X上的偏序(Partial Order),如果对每个x,y属于X必有xRy 或 yRx,则称R是集合X上的全序关系。
注意: ①若将图中顶点按拓扑次序排成一行,则图中所有的有向边均是从左指向右的。
②若图中存在有向环,则不可能使顶点满足拓扑次序。
③一个DAG的拓扑序列通常表示某种方案切实可行。
求C语言高手!数据结构的拓扑排序
算法 1.无前趋的顶点优先: (1)算法描述: (a)从网中选择一个入度为零的顶点输出; (b)删除该顶点及其于该点有关的所有边; (c)是否还有入度为零的顶点?若有,执行(a),否则结束。算法实现 以邻接表为图的存储结构的算法: a)扫描顶点表,将入度为零的顶点入栈; b)当栈非空时: 输出栈顶元素v,出栈; 检查v的出边,将每条出边的终端顶点的入度减1,若该顶点入度为0,入栈; c)当栈空时,若输出的顶点小于顶点数,则说明AOV网有回路,否则拓扑排序完成。
算法实现: void Graph::Toplogicasort()/是入度为0的顶点栈的栈顶指针 { =-1; for(int i=0;i<n;i++) //建立如度为0顶点的链栈 if (count[i]==0) { count[i]; =i; } for(int i=0;i<n;i++) ==-1) { cout<<"Network has a cycle"<<endl; return; } else { int =];//入度为0的顶点出栈 count<<j<<endl; Edge<float> *l=NodeTable[j].adj; while(l) { int k=l,dest; if(--count[k]==0) { count[k];//入度减至0的顶点进栈 =k; } l=l->link;//取j的下一条出边 } } } /*通常的拓扑算法要用两个数组,一个用来记录每个顶点的入度,当入度为0,则进栈 。
另一个数组用作栈数组,记录入度为0的顶点。
其实当入度为0的顶点进栈以后,count[i] =0就不再有用,所以可以用count[i]记录栈内下一个入度为0的顶点指向栈顶顶点号 */
怎样实现c语言的拓扑排序啊,谁能帮我写一下代码啊 谢谢啊
#include拓扑排序时间复杂度o(n+e)怎么算的?
对有n个顶点和e条弧的有向图而言,建立求各顶点的入度的时间复杂度为O(e);建零入度顶点栈的时间复杂度为O(n);在拓扑排序过程中,若有向图无环,则每个顶点进一次栈、出一次栈,入度减1的操作在while语句中总共执行e次,所以总的时间复杂度为O(n+e)。对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。
通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。
简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
时间复杂度是同一问题可用不同算法解决,而一个算法的质量优劣将影响到算法乃至程序的效率。
算法分析的目的在于选择合适算法和改进算法。
计算机科学中,算法的时间复杂度是一个函数,它定性描述了该算法的运行时间。
这是一个关于代表算法输入值的字符串的长度的函数。
时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。
使用这种方式时,时间复杂度可被称为是渐近的,它考察当输入值大小趋近无穷时的情况。
扩展资料 在计算时间复杂度的时候,先找出算法的基本操作,然后根据相应的各语句确定它的执行次数,再找出 T(n) 的同数量级,找出后,f(n) = 该数量级,若 T(n)/f(n) 求极限可得到一常数c,则时间复杂度T(n) = O(f(n))。
按数量级递增排列,常见的时间复杂度有: 常数阶O(1),线性阶O(n), 线性对数阶O(nlog2n),平方阶O(n^2),立方阶O(n^3),..., k次方阶O(n^k),指数阶O(2^n)。
随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。
参考资料来源:百度百科-拓扑排序 参考资料来源:百度百科-时间复杂度
- 拓扑排序拓扑排序时间复杂度o(n+e)怎么算的?相关文档
- 拓扑排序什么是逆拓扑排序
- 拓扑排序数据结构的课程设计-拓扑排序的算法
Vultr新用户省钱福利,最新可用优惠码/优惠券更新
如今我们无论线上还是线下选择商品的时候是不是习惯问问是不是有优惠活动,如果有的话会加速购买欲望。同样的,如果我们有准备选择Vultr商家云服务器的时候,也会问问是不是有Vultr优惠码或者优惠券这类。确实,目前Vultr商家有一些时候会有针对新注册用户赠送一定的优惠券活动。那就定期抽点时间在这篇文章中专门整理最新可用Vultr优惠码和商家促销活动。不过需要令我们老用户失望的,至少近五年我们看到Vu...

月费$389,RackNerd美国大硬盘独立服务器
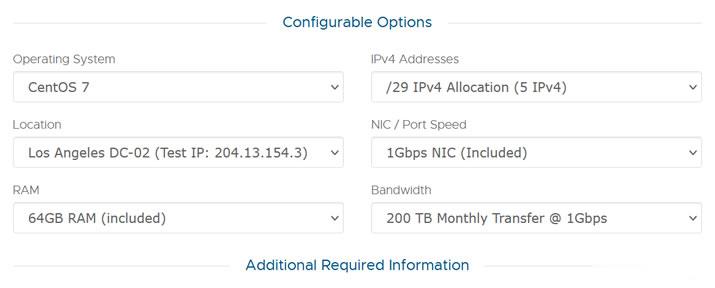
这次RackNerd商家提供的美国大硬盘独立服务器,数据中心位于洛杉矶multacom,可选Windows、Linux镜像系统,默认内存是64GB,也可升级至128GB内存,而且硬盘采用的是256G SSD系统盘+10个16TSAS数据盘,端口提供的是1Gbps带宽,每月提供200TB,且包含5个IPv4,如果有需要更多IP,也可以升级增加。CPU核心内存硬盘流量带宽价格选择2XE5-2640V2...
RAKsmart 黑色星期五云服务器七折优惠 站群服务器首月半价
一年一度的黑色星期五和网络星期一活动陆续到来,看到各大服务商都有发布促销活动。同时RAKsmart商家我们也是比较熟悉的,这次是继双十一活动之后的促销活动。在活动产品中基本上沿袭双11的活动策略,比如有提供云服务器七折优惠,站群服务器首月半价、还有新人赠送红包等活动。如果我们有需要RAKsmart商家VPS、云服务器、独立服务器等产品的可以看看他们家的活动。这次活动截止到11月30日。第一、限时限...
拓扑排序为你推荐
-
excel通配符EXCEL中通配符初始化磁盘win10新装硬盘初始化?初始化磁盘如何将磁盘还原为“未初始化”状态?provisionedNIST的云计算定义订单详情请问拼多多如何查看订单详情?怎么将购买的订单详情全部导出?巴西时区巴西与中国的时差是多少运行时错误1004ipad下载时出现错误1004是怎么回事?该怎么解决?qsv视频格式转换器手机qsv怎么转换成mp4格式转换器网页错误详细信息我为什么不可以收货那 网页错误详细信息眼镜片品牌镜片哪个牌子好,十大光学镜片品牌排名推荐