函数2020-2021学年陕西西安高一上数学月考试卷及答案
2.下列五个写法①{0}∈{1,2,3} ②⌀⊆{0} ③{0, 1 ,2}⊆{1,2,0} ④0∈⌀ ⑤0∩⌀=⌀ 其中错误写法的个数
为( )
A.1 B.2 C.3 D.4 8.下列函数中是同一函数的是( )
A.y=x2与y=x|x| B.y=x2与y=(x)2
3.集合{1,2,3}的所有真子集的个数为 C.y=x2+xx与y=x+1 D.y=2x+1与y=2t+1
A.3 B.6 C.7 D.8
4.设集合A={x|x<3} B={1,2,3,4} 则A∩B=( ) 9.已知函数y=x2+1 x≤0 −2xx>0 则使函数值为5的x的值是( )
A.0 B.0,1 C.1,2 D.0,1,2 A.−2或2 B.2或−52 C.−2 D.2或−2或−52
5.函数f(x)=x−1x−2的定义域为( ) 10.设A={x|0≤x≤6} B={y|0≤y≤2} 下列从A到B的对应法则f不是映射的是( )
A.(1,+∞) B.[1,+∞) C.[1,2) D.[1,2)∪(2,+∞) A.f:x→y=13x B.f:x→y=12x C.f:x→y=14x D.f:x→y=16x
二、填空题
6.设f(x)=x+2 x≥0 1 x<0 则f(f(−1))=( )
A.3 B.1 C.0 D.−1 在映射f:A→B中A=B=R且f (x,y)→(x−y,x+y) 则与A中的元素(2, 1)在B中的象为________.
7.下列四个图形中不是以x为自变量的函数的图象是 含有三个实数的集合既可表示成{a,ba,1} 又可表示成{a2,a+b,0} 则a2013+b2014=________二次函数y=2x2的图像向上平移2个单位长度再向右平移1个单位长度所得图像对应的函数解析式________.
已知函数fx=x2−21−ax+2在(−∞,4]上是减函数则实数a的取值范围为________.
三、解答题
集合A={x|3≤x<10} B={x|1<3x−5<16}.
(1)求A∪B
(2)求∁RA∩B.
求下列函数的解析式
(1)已知fx+1=x+2x求fx
(2)已知3fx+2f−x=x+3 求fx.
已知函数f(x)=4x2−6x+2
(1)求f(x)的单调区间
(2)f(x)在[2,4]上的最大值
设函数f(x)=1+mx且f(1)=2.
(1)求m的值
(2)试判断f(x)在(0,+∞)上的单调性并用定义加以证明
(3)若x∈[2,5]求值域.
参考答案与试题解析 3.
2020-2021学年陕西西安高一上数学月考试卷 【答案】
一、选择题 C
1 . 【考点】
【答案】 子集与真子集
C
包括空集集合的相等
个分别对①②③④进行分析从而得出答案 故选C
【解答】 4.
解①中M是数集包含2个元素P是点集只有1个元素故不是同一集合 【答案】
②中M是点集包含1个元素P也是点集包含1个元素但是(3, 1)与(1,3)不是同一个点故不是同一 C
集合 一 【考点】
其运算
故选C. 【解析】
2. 无
【解答】
集合的包含关系判断及应用 故选C
元素与集合关系的判断 5.
【解析】 【答案】
D
元素与集合的关系是∈和∉ 集合间的关系是⊆、 ⊇、 ⊊、 ⊋、 ⊈、 = 根据这些逐个判断
【解答】
解①{0}和{1,2,3}都是集合不能用“∈” 故不正确
②⌀⊆{0} 空集是任何集合的子集故正确 【解析】
③{0, 1 ,2}⊆{1,2,0}两集合的元素相等也可用“⊆”表示故正确 根据二次根式的性质以及分母不是0 求出函数的定义域即可【解答】
综上错误的个数为3. 解由题意得
故选C x−1≥0 x−2≠0 解得x≥1且x≠2
故函数的定义域是[1,2)∪(2,+∞). 【解答】
故选D. 解在A选项中前者的y属于非负数后者的y∈R两个函数的值域不同
6. 在B选项中前者的定义域x∈R后者的x∈(0,+∞) 定义域不同
【答案】 在C选项中前者定义域为一x≠0 后者为x∈R定义域不同
A 在D选项中两个函数是同 个函数.
故选D
【考点】 9.
分段函数的应用 【答案】
【解析】 C
根据分段函数的定义域分别代入自变量的值求解即可 【考点】
【解答】 函数的求值
解 ∵−f(x=)=x+2= x≥=0 1 x<0 【解析】
7. 【解答】
【答案】 解由题意当x≤0时 f(x)=x2+1=5 得x=±2.
C 又x≤0 所以x=−2
去
函数的概念及其构成要素 10.
【解析】 【答案】
根据函数的定义中“定义域内的每一个x都有唯一函数值与之对应”判断 B
【解答】 【考点】
解由函数定义知定义域内的每一个x都有唯一函数值与之对应 映射
A、 B、 D选项中的图象都符合C项中对于大于零的x而言有两个不同的值与之对应不符合函数定义 【解析】
故选C
8. 通过举反例按照对应法则f 集合A中的元素6 在后一个集合B中没有元素与之对应故选项A不是映
射从而选出答案
【考点】
判断两个函数是否为同一函数 故不满足映射的定义
【解析】 ACD是映射
此题暂无解析
在后一个集合B中都有唯一的一个元素与之对应 则a2013+b2014=(−1)2013+02014=−1 .
故BCD满足映射的定义. 故答案为−1
故选B 【答案】
二、填空题 y=2x−12+2
【答案】 【考点】
(1,3) 函数的图象与图象变化
【考点】 【解析】
个单位长度得到的函数【解析】 y=2x−12+2.
由题意x=2 y=1 则x−y=1 x+y=3 即可得出结论 【解答】
【解答】 解函数y=2x2的图像向上平移2个单位长度得到函数y=2x2+2的图像
再向右平移1个单位长度得到的函数解析式为y=2x−12+2.
.
故答案为 (1,3) 【答案】a≤−3
【答案】
−1 【考点】
二次函数的性质
【考点】
有理数指数幂的化简求值 【解析】
集合的相等 无
【解析】 【解答】
a2012+b2013中计算可得答案 三、解答题
【解答】 【答案】
解根据题意由{a,ba, 1}={a2,a+b,0} 可得a=0或ba=0 解 (1)B={x|2<x<7}
又由ba的意义则a≠0 必有ba=0 ∴ A∪B={x|2<x<10}
则b=0 (2)∁RA={x|x<3或x≥10} (∁RA)∩B={x|2<x<3}
【考点】
集合{a,0, 1}中 a≠1 交、并、补集的混合运算
则必有a=−1 并集及其运算
【解析】 二次函数在闭区间上的最值
1 答案未提供解析 【解析】
2答案未提供解析 1 2配方利用二次函数的单调性即可得出【解答】 【解答】
∴ A∪B={x|2<x<10} ∴ 函数f(x)在区间(−∞,34)上单调递减在区间[34 +∞)上单调递增
(2)∁RA={x|x<3或x≥10} (∁RA)∩B={x|2<x<3}
【答案】 ∴ 当x=4时函数f(x)取得最大值 f(4)=4×42−6×4+2=42 解 (1)由fx+1=x+2x 【答案】
(2)根
【考点】 设0<x1<x2
函数解析式的求解及常用方法
【解析】 所以f(x1)−f(x2)>0 即f(x1)>f(x2)
无 所以函数f(x)在(0,+∞)上单调递减.
无 (3)由于函数f(x)在(0,+∞)上单调递减
所以f(x)max=f(2)=1+12=32,
【解答】 f(x)min=f(5)=1+15=65
解 (1)由fx+1=x+2x 所以函数的值域为[65,32].
得 fx+1=x+2x+1−1=x+12−1x≥0
因x+1≥1 则fx=x2−1 x≥1
(2)根据条件 3fx+2f−x=x+3,3f−x+2fx=−x+3, 函数单调性的判断与证明
解得fx=x+35
函数的求值
【答案】 函数的值域及其求法
【解析】
(2)由(1)可知 f(x)在[2,4]上单调递增 此题暂无解析
∴ 当x=4时函数f(x)取得最大值 f(4)=4×42−6×4+2=42 【解答】
【考点】 解 (1)由f(1)=2
二次函数的性质 得1+m=2, m=1 .
(2)f(x)在(0,+∞)上单调递减.
证明由(1)知 f(x)=1+1x
设0<x1<x2
则f(x1)−f(x2)=(1+1 x1)−(1+1 x2)=x2−x1 x1 x2.
因为0<x1<x2 所以x2−x1>0, x1 x2>0
所以f(x1)−f(x2)>0 即f(x1)>f(x2)
所以函数f(x)在(0,+∞)上单调递减.
(3)由于函数f(x)在(0,+∞)上单调递减
所以f(x)max=f(2)=1+12=32,f(x)min=f(5)=1+15=65
所以函数的值域为[65,32].
- 函数2020-2021学年陕西西安高一上数学月考试卷及答案相关文档
- 英语2020-2021学年陕西西安市长安区第一中学高一上学期期中考试英语试题(解析版)
- 万元陕西服务器建设项目投资计划书
- 万元陕西服务器建设项目可行性研究报告
- 北山陕西高文古诗鉴赏练习试题附答案
- 项目陕西高密度印制电路板项目可行性研究报告
- 的是陕西师大附中高理综模拟试题
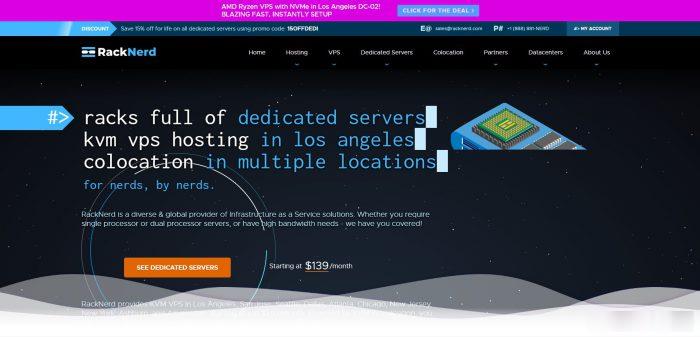
创梦网络-江苏宿迁BGP云服务器100G高防资源,全程ceph集群存储,安全可靠,数据有保证,防护真实,现在购买7折促销,续费同价!
官方网站:点击访问创梦网络宿迁BGP高防活动方案:机房CPU内存硬盘带宽IP防护流量原价活动价开通方式宿迁BGP4vCPU4G40G+50G20Mbps1个100G不限流量299元/月 209.3元/月点击自助购买成都电信优化线路8vCPU8G40G+50G20Mbps1个100G不限流量399元/月 279.3元/月点击自助购买成都电信优化线路8vCPU16G40G+50G2...
RackNerd:特价美国服务器促销,高配低价,美国多机房可选择,双E526**+AMD3700+NVMe
racknerd怎么样?racknerd今天发布了几款美国特价独立服务器的促销,本次商家主推高配置的服务器,各个配置给的都比较高,有Intel和AMD两种,硬盘也有NVMe和SSD等多咱组合可以选择,机房目前有夏洛特、洛杉矶、犹他州可以选择,性价比很高,有需要独服的朋友可以看看。点击进入:racknerd官方网站RackNerd暑假独服促销:CPU:双E5-2680v3 (24核心,48线程)内存...
创梦网络-四川大带宽、镇江电信服务器云服务器低至56元
达州创梦网络怎么样,达州创梦网络公司位于四川省达州市,属于四川本地企业,资质齐全,IDC/ISP均有,从创梦网络这边租的服务器均可以备案,属于一手资源,高防机柜、大带宽、高防IP业务,一手整C IP段,四川电信,一手四川托管服务商,成都优化线路,机柜租用、服务器云服务器租用,适合建站做游戏,不须要在套CDN,全国访问快,直连省骨干,大网封UDP,无视UDP攻击,机房集群高达1.2TB,单机可提供1...
-
朝阳分局犯罪嫌疑人标准化信息采集系统pqqgraphpreloadedbaidu支持ipad支持ipad支持ipadtracerouteLinux 下traceroute的工作原理是什么 !tracerouteping命令和traceroute(tracert )在功能上的区别有哪些?ipadwifiIPAD连上了WIFI,但是无法上网,急!!css下拉菜单如何使用HTML和CSS制作下拉菜单