dominated腾讯qq好友恢复
腾讯qq好友恢复 时间:2021-05-25 阅读:()
Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePetersa,PedroBicudob,KrzysztofCichya,c,BjrnWagenbacha,MarcWagneraaGoethe-UniversittFrankfurtamMain,InstitutfürTheoretischePhysik,Max-von-Laue-Strae1,D-60438FrankfurtamMain,GermanybCFTP,DepartamentodeFísica,InstitutoSuperiorTécnico,UniversidadedeLisboa,AvenidaRoviscoPais,1049-001Lisboa,PortugalcAdamMickiewiczUniversity,FacultyofPhysics,Umultowska85,61-614Poznan,PolandE-mail:peters@th.
physik.
uni-frankfurt.
de,bicudo@tecnico.
ulisboa.
pt,kcichy@th.
physik.
uni-frankfurt.
de,wagenbach@th.
physik.
uni-frankfurt.
de,mwagner@th.
physik.
uni-frankfurt.
deWecomputepotentialsoftwostaticantiquarksinthepresenceoftwoquarksqqofnitemassusinglatticeQCD.
InasecondstepwesolvetheSchrdingerequation,todetermine,whethertheresultingpotentialsaresufcientlyattractivetohostaboundstate,whichwouldindicatetheexistenceofastableqqbbtetraquark.
Wendaboundstateforqq=(uddu)/√2withcorrespondingquantumnumbersI(JP)=0(1+)andevidenceagainsttheexistenceofboundstateswithisospinI=1orqq∈{cc,ss}.
The33rdInternationalSymposiumonLatticeFieldTheory14-18July2015KobeInternationalConferenceCenter,Kobe,JapanSpeaker.
cCopyrightownedbytheauthor(s)underthetermsoftheCreativeCommonsAttribution-NonCommercial-ShareAlikeLicence.
http://pos.
sissa.
it/arXiv:1508.
00343v1[hep-lat]3Aug2015Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePeters1.
MotivationAnumberofmesonsobservedinexperimentslikeLHCborBellearenotwellunderstood.
Thosemesonshavemassesandquantumnumbers,whicharenottypicalforstandardquark-antiquarkstates,butindicateanexoticfour-quarkstructure.
Prominentexamplesarethechargedcharmonium-likeandbottomonium-likestatesZc±andZb±(cf.
e.
g.
[1]).
Theirmassesanddecayproductssuggestthepresenceofaccorbbpair,respectively.
Ontheotherhandtheirelectricchargeindicatesadditionallyalightquark-antiquarkpairudordu.
Thosefour-quarksystems,inthefol-lowingalsoreferredtoastetraquarks,areexpectedtobestudiedinmoredetailinthenearfuturebyexperimentalcollaborations.
Therefore,asoundtheoreticalunderstandingofthosesystemsiscrucialandofgreatinterest.
Herewesummarizethemainresultsofourrecentlypublishedwork[2],wherewehavestudiedfour-quarksystemswithtwoheavyantiquarksbbandtwolighterquarksqqusinglatticeQCDandtheBorn-Oppenheimerapproximation.
Firstbbpotentialsinthepresenceoflighterquarksqqarecomputed.
ThentheSchrdingerequationissolvedusingthesepotentials,wherepossiblyexistingboundstatesindicatestabletetraquarks.
Otherpapersstudyingthesamesystemswithsimilarmethodsinclude[3,4,5,6,7,8,9,10,11,12,13,14].
2.
QualitativediscussionofqqbbsystemsAtsmallbbseparationsthebbinteractionisdominatedby1-gluonexchange.
Foraboundstatethebbpairmust,therefore,beinanattractivecolortriplet.
DuetothePauliprincipleandbecauseweassumeaspatiallysymmetrics-wave,bbhastoformanantisymmetriccolor-spin-avorcombinationand,hence,asymmetricspincombination,i.
e.
bbspinjb=1.
Sincethecompletefour-quarksystemiscolorneutral,thelightquarksqqmustbeinanantisymmetriccolorantitriplet.
AgainduetothePauliprincipleqqhastoformanantisymmetriccolor-spin-avorcombinationand,hence,asymmetricspin-avorcombination.
Candidatesfortetraquarksare,therefore,the(spin)scalarisosinglet(i.
e.
aqqspinsingletj=0withantisymmetricavor,e.
g.
qq∈{(uddu)/√2,(s(1)s(2)s(2)s(1))/√2,(c(1)c(2)c(2)c(1))/√2}1)andthe(spin)vectorisotriplet(i.
e.
aqqspintripletj=1withsymmetricavor,e.
g.
qq∈{uu,(ud+du)/√2,dd,ss,cc}).
TheoverallquantumnumbersofaboundqqbbsystemareI(JP)=0(1+)forthescalarisosingletchannelandI(JP)∈{1(0+),1(1+),1(2+)}forthevectorisotripletchannel.
Atlargebbseparationsthebbinteractionisscreenedbythelightquarksqq,i.
e.
thefourquarksformasystemoftwoheavy-lightmesons.
Oneexpectsstrongerscreeningforincreasingquarkmassmq,becausethewavefunctionsofthecorrespondingmesonsqbarethenmorecompact.
3.
LatticeQCDcomputationofstaticantiquark-antiquarkpotentialsWeextractpotentialsoftwostaticantiquarksQQ(approximatingthetwobquarksoftheqqbbsystem)inthepresenceoftwolightquarksqqfromcorrelationfunctionsC(t,r)=|O(t)O(0)|∝t→∞exp(V(r)t).
(3.
1)1Tobeabletostudyavorantisymmetricqqcombinationswithq=s,weconsidertwohypotheticaldegenerateavorswiththemassofthesquark,s(1)ands(2),andsimilarlyforq=c,c(1)andc(2).
2Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePetersOdenotesafour-quarkcreationoperator,O=(CΓ)AB(CΓ)CDQC(r1)q(1)A(r1)QD(r2)q(2)B(r2),r=|r1r2|,(3.
2)whereΓisanappropriatecombinationofγmatricesaccountingfordenedquantumnumberslightquarkspin|jz|,parityPandPx(cf.
[8]fordetails).
Γ∈{(1γ0)γ5,(1γ0)γj}doesnotaffecttheresultingpotentialV(r),sincethestaticquarkspinisirrelevant.
C=γ0γ2denotesthechargeconjugationmatrix.
Notethatoperatorslike(3.
2)generateoverlapnotonlytomesonicmoleculestructures,butalsotodiquark-antidiquarkstructures[15,16].
Theasymptoticvalueofapotentialandwhetheritisattractiveorrepulsivedependsonthequantumnumbers(|jz|,P,Px)and,hence,onΓ.
Inthefollowingweareexclusivelyinterestedinat-tractivepotentialsbetweentwogroundstatestatic-lightmesons:thescalarisosingletcorrespondingtoΓ=(1+γ0)γ5andthevectorisotripletcorrespondingtoΓ=(1+γ0)γj.
Computationshavebeenperformedusingtwoensemblesofgaugelinkcongurationsgener-atedbytheEuropeanTwistedMassCollaboration(ETMC)withdynamicalu/dquarks.
Informa-tionontheseensemblescanbefoundinTable1and[17,18].
βlatticesizelainfmmπinMeV#congurations3.
90243*480.
004000.
0793404804.
35323*640.
001750.
042352100Table1:Ensemblesofgaugelinkcongurations(β:inversegaugecoupling;l:bareu/dquarkmassinlatticeunits;a:latticespacing;mπ:pionmass).
4.
qqbbtetraquarksintheBorn-OppenheimerapproximationTodetermineananalyticalexpressionfortheQQpotentialorequivalentlybbpotential,wettheansatzV(r)=αrexprd2+V0(4.
1)withrespecttoα,dandV0tothelatticeQCDresultsobtainedintheprevioussection.
TheconstantV0accountsfortwicethemassofthegroundstatestatic-lightmeson.
Weinsertthetheanalyticalexpression(4.
1)intheSchrdingerequationfortheradialcoordi-nateofthetwobquarks(whichweassumetobeinans-wave),12d2dr2+U(r)R(r)=EBR(r)(4.
2)withU(r)=V(r)|V0=0and=mb/2anddeterminethelowesteigenvalueEB.
IfEB0,thereisnobinding,i.
e.
thefour-quarksystemwillalwaysbeasystemoftwounboundBmesons.
Noticethatthisso-calledBorn-Oppenheimerapproximationisvalidformqmb,whichiscertainlythecaseforq∈{u,d,s}andatleastcrudelyfullledforq=c.
Toquantifythesystematicerrorsofdifferentchannels(scalarisosingletandvectorisotriplet,differentlightavorsq∈{u,d,s,c}),weperformalargenumberoftsvaryingtherangeof3Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePeterstemporalseparationstmin≤t≤tmaxofthecorrelationfunctionC(t,r)(cf.
eq.
(3.
1)),atwhichthelatticepotentialisreadoff,aswellastherangeofspatialbbseparationsrmin≤r≤rmaxconsideredintheχ2minimizingtofeq.
(4.
1)tothelatticepotential.
Detailsonthisparametervariationcanbefoundin[2].
Foreachsetofinputparameters(tmin,tmax,rmin,rmax)wedetermineα,dandEB.
Thenwegeneratehistogramsforα,dandEBweightedaccordingtothecorrespondingχ2/dof.
Thewidthsofthesehistogramsaretakenassystematicerrorsofα,dandEB[19],whilethestatisticalerrorsareobtainedviaajackknifeanalysis.
InFigure1examplehistogramsforthescalarisosingletforqq=udareshown.
Figure1:Histogramsforthescalarisosingletforqq=ud.
Thered/green/bluebarsindicatethestatistical/systematic/combinederrors.
Theresultingpotentialstsfordifferentchannels,i.
e.
eq.
(4.
1)withcorrespondingvaluesforαandd,arecollectedinFigure2.
Theerrorbandsrepresentthecombinedsystematicandstatisticalerrors.
Onecanobservethatthepotentialsarewideranddeeperforlighterqqquarkmasses.
Moreover,thescalarchannelsaremoreattractivethantherespectivevectorchannels.
Correspondingly,itturnsoutthatthereisaboundstateonlyforthescalarisosingletwithqq=udwithbindingenergyEB=93+4743MeV,i.
e.
aboundstatewitharound2σcondencelevel.
InFigure3wepresentourresultsinanalternativegraphicalway.
Thethreeplotscorrespondtou/d,sandclightquarksqq,respectively.
Eachtofeq.
(4.
1)tolatticepotentialresultsisrepresentedbyadot(red:scalarchannels;green:vectorchannels;crosses:rmin=2a;boxes:rmin=3a).
Theextensionsofthepointcloudsrepresentthesystematicuncertaintieswithrespecttoαandd.
IfapointcloudislocalizedaboveorleftoftheisolinewithEB=0.
1MeV(essentiallythebindingthreshold),thecorrespondingfourquarksqqbbcannotformaboundstate.
Alocalizationbeloworrightofthatisolineisastrongindicationfortheexistenceofatetraquark.
Againthereisclearevidenceforatetraquarkstateinthescalaru/dchannel.
Thescalarschannelisslightlyabove,butratherclosetothebindingthreshold.
Thescalarcandallvectorchannelsclearlydonothostboundfour-quarkstates.
5.
SummaryandoutlookWehavefoundaudbbtetraquarkwithquantumnumbersI(JP)=0(1+)(i.
e.
inthescalarisosingletchannelwithqq=ud)withacondencelevelofaround2σ.
Thereseemtoexistno4Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePetersFigure2:Potentialstsfordifferentchannels(upperline:scalarisosinglet;lowerline:vectorisotriplet).
Thecurveswithoutanerrorbandarecopiedfromtherespectiveotherplotsinthesamelineforeasycomparison.
Verticallinesindicatetheavailablelatticebbseparations.
tetraquarksfortheotherchannels.
InthisworklatticeQCDcomputationshavebeenperformedforlightu/dquarkscorrespond-ingtomπ≈340MeV.
Weplantorepeattheanalysisforatleastanotherpionmassandthenextrapolatetothephysicalpoint.
Itwillthenbemostinterestingtocheck,whetheraboundstatewillalsoappearinthevectorisotripletchannelwithqq=ud.
AnotheraspectistoinvestigatethestructureofthefoundI(JP)=0(1+)tetraquark,i.
e.
toexplore,whetheritisratheramesonicmoleculeoradiquark-antidiquarkpair.
Wealsoplantoincludecorrectionsduetotheheavyquarkspins(forrstpreliminaryresultscf.
[14]).
Finally,oneshouldstudytheexperimentallymoreaccessible,buttheoreticallymorechallengingcaseofqqbbsystems.
AcknowledgmentsP.
B.
thanksIFTforhospitalityandCFTP,grantFCTUID/FIS/00777/2013,forsupport.
M.
W.
andA.
P.
acknowledgesupportbytheEmmyNoetherProgrammeoftheDFG(GermanResearchFoundation),grantWA3000/1-1.
ThisworkwassupportedinpartbytheHelmholtzInternationalCenterforFAIRwithintheframeworkoftheLOEWEprogramlaunchedbytheStateofHesse.
5Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePetersFigure3:BindingenergyisolinesEB=constantintheα-d-planeforu/d,sandclightquarksqqtogetherwiththetresultsofeq.
(4.
1)tolatticepotentials.
6Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePetersCalculationsontheLOEWE-CSChigh-performancecomputerofJohannWolfgangGoethe-UniversityFrankfurtamMainwereconductedforthisresearch.
WewouldliketothankHPC-Hessen,fundedbytheStateMinistryofHigherEducation,ResearchandtheArts,forprogrammingadvice.
References[1]A.
Bondaretal.
[BelleCollaboration],Phys.
Rev.
Lett.
108,122001(2012)[arXiv:1110.
2251[hep-ex]].
[2]P.
Bicudo,K.
Cichy,A.
Peters,B.
WagenbachandM.
Wagner,Phys.
Rev.
D92,014507(2015)[arXiv:1505.
00613[hep-lat]].
[3]C.
StewartandR.
Koniuk,Phys.
Rev.
D57,5581(1998)[arXiv:hep-lat/9803003].
[4]C.
MichaelandP.
Pennanen[UKQCDCollaboration],Phys.
Rev.
D60,054012(1999)[arXiv:hep-lat/9901007].
[5]M.
S.
CookandH.
R.
Fiebig,arXiv:hep-lat/0210054.
[6]T.
Doi,T.
T.
TakahashiandH.
Suganuma,AIPConf.
Proc.
842,246(2006)[arXiv:hep-lat/0601008].
[7]W.
Detmold,K.
OrginosandM.
J.
Savage,Phys.
Rev.
D76,114503(2007)[arXiv:hep-lat/0703009].
[8]M.
Wagner[ETMCollaboration],PoSLATTICE2010,162(2010)[arXiv:1008.
1538[hep-lat]].
[9]G.
BaliandM.
Hetzenegger,PoSLATTICE2010,142(2010)[arXiv:1011.
0571[hep-lat]].
[10]M.
Wagner[ETMCollaboration],ActaPhys.
Polon.
Supp.
4,747(2011)[arXiv:1103.
5147[hep-lat]].
[11]P.
BicudoandM.
Wagner,Phys.
Rev.
D87,114511(2013)[arXiv:1209.
6274[hep-ph]].
[12]Z.
S.
BrownandK.
Orginos,Phys.
Rev.
D86,114506(2012)[arXiv:1210.
1953[hep-lat]].
[13]B.
Wagenbach,P.
BicudoandM.
Wagner,J.
Phys.
Conf.
Ser.
599,012006(2015)[arXiv:1411.
2453[hep-lat]].
[14]J.
Scheunert,P.
Bicudo,A.
UenverandM.
Wagner,arXiv:1505.
03496[hep-ph].
[15]C.
Alexandrou,J.
O.
Daldrop,M.
DallaBrida,M.
Gravina,L.
Scorzato,C.
UrbachandM.
Wagner,[ETMCollaboration],JHEP1304,137(2013)[arXiv:1212.
1418].
[16]A.
Abdel-Rehim,C.
Alexandrou,J.
Berlin,M.
DallaBrida,M.
GravinaandM.
Wagner,PoSLATTICE2014,104(2014)[arXiv:1410.
8757[hep-lat]].
[17]P.
Boucaudetal.
[ETMCollaboration],Comput.
Phys.
Commun.
179,695(2008)[arXiv:0803.
0224[hep-lat]].
[18]R.
Baronetal.
[ETMCollaboration],JHEP1008,097(2010)[arXiv:0911.
5061[hep-lat]].
[19]K.
Cichy,V.
Drach,E.
Garcia-Ramos,G.
HerdoizaandK.
Jansen,Nucl.
Phys.
B869,131(2013)[arXiv:1211.
1605[hep-lat]].
7
physik.
uni-frankfurt.
de,bicudo@tecnico.
ulisboa.
pt,kcichy@th.
physik.
uni-frankfurt.
de,wagenbach@th.
physik.
uni-frankfurt.
de,mwagner@th.
physik.
uni-frankfurt.
deWecomputepotentialsoftwostaticantiquarksinthepresenceoftwoquarksqqofnitemassusinglatticeQCD.
InasecondstepwesolvetheSchrdingerequation,todetermine,whethertheresultingpotentialsaresufcientlyattractivetohostaboundstate,whichwouldindicatetheexistenceofastableqqbbtetraquark.
Wendaboundstateforqq=(uddu)/√2withcorrespondingquantumnumbersI(JP)=0(1+)andevidenceagainsttheexistenceofboundstateswithisospinI=1orqq∈{cc,ss}.
The33rdInternationalSymposiumonLatticeFieldTheory14-18July2015KobeInternationalConferenceCenter,Kobe,JapanSpeaker.
cCopyrightownedbytheauthor(s)underthetermsoftheCreativeCommonsAttribution-NonCommercial-ShareAlikeLicence.
http://pos.
sissa.
it/arXiv:1508.
00343v1[hep-lat]3Aug2015Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePeters1.
MotivationAnumberofmesonsobservedinexperimentslikeLHCborBellearenotwellunderstood.
Thosemesonshavemassesandquantumnumbers,whicharenottypicalforstandardquark-antiquarkstates,butindicateanexoticfour-quarkstructure.
Prominentexamplesarethechargedcharmonium-likeandbottomonium-likestatesZc±andZb±(cf.
e.
g.
[1]).
Theirmassesanddecayproductssuggestthepresenceofaccorbbpair,respectively.
Ontheotherhandtheirelectricchargeindicatesadditionallyalightquark-antiquarkpairudordu.
Thosefour-quarksystems,inthefol-lowingalsoreferredtoastetraquarks,areexpectedtobestudiedinmoredetailinthenearfuturebyexperimentalcollaborations.
Therefore,asoundtheoreticalunderstandingofthosesystemsiscrucialandofgreatinterest.
Herewesummarizethemainresultsofourrecentlypublishedwork[2],wherewehavestudiedfour-quarksystemswithtwoheavyantiquarksbbandtwolighterquarksqqusinglatticeQCDandtheBorn-Oppenheimerapproximation.
Firstbbpotentialsinthepresenceoflighterquarksqqarecomputed.
ThentheSchrdingerequationissolvedusingthesepotentials,wherepossiblyexistingboundstatesindicatestabletetraquarks.
Otherpapersstudyingthesamesystemswithsimilarmethodsinclude[3,4,5,6,7,8,9,10,11,12,13,14].
2.
QualitativediscussionofqqbbsystemsAtsmallbbseparationsthebbinteractionisdominatedby1-gluonexchange.
Foraboundstatethebbpairmust,therefore,beinanattractivecolortriplet.
DuetothePauliprincipleandbecauseweassumeaspatiallysymmetrics-wave,bbhastoformanantisymmetriccolor-spin-avorcombinationand,hence,asymmetricspincombination,i.
e.
bbspinjb=1.
Sincethecompletefour-quarksystemiscolorneutral,thelightquarksqqmustbeinanantisymmetriccolorantitriplet.
AgainduetothePauliprincipleqqhastoformanantisymmetriccolor-spin-avorcombinationand,hence,asymmetricspin-avorcombination.
Candidatesfortetraquarksare,therefore,the(spin)scalarisosinglet(i.
e.
aqqspinsingletj=0withantisymmetricavor,e.
g.
qq∈{(uddu)/√2,(s(1)s(2)s(2)s(1))/√2,(c(1)c(2)c(2)c(1))/√2}1)andthe(spin)vectorisotriplet(i.
e.
aqqspintripletj=1withsymmetricavor,e.
g.
qq∈{uu,(ud+du)/√2,dd,ss,cc}).
TheoverallquantumnumbersofaboundqqbbsystemareI(JP)=0(1+)forthescalarisosingletchannelandI(JP)∈{1(0+),1(1+),1(2+)}forthevectorisotripletchannel.
Atlargebbseparationsthebbinteractionisscreenedbythelightquarksqq,i.
e.
thefourquarksformasystemoftwoheavy-lightmesons.
Oneexpectsstrongerscreeningforincreasingquarkmassmq,becausethewavefunctionsofthecorrespondingmesonsqbarethenmorecompact.
3.
LatticeQCDcomputationofstaticantiquark-antiquarkpotentialsWeextractpotentialsoftwostaticantiquarksQQ(approximatingthetwobquarksoftheqqbbsystem)inthepresenceoftwolightquarksqqfromcorrelationfunctionsC(t,r)=|O(t)O(0)|∝t→∞exp(V(r)t).
(3.
1)1Tobeabletostudyavorantisymmetricqqcombinationswithq=s,weconsidertwohypotheticaldegenerateavorswiththemassofthesquark,s(1)ands(2),andsimilarlyforq=c,c(1)andc(2).
2Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePetersOdenotesafour-quarkcreationoperator,O=(CΓ)AB(CΓ)CDQC(r1)q(1)A(r1)QD(r2)q(2)B(r2),r=|r1r2|,(3.
2)whereΓisanappropriatecombinationofγmatricesaccountingfordenedquantumnumberslightquarkspin|jz|,parityPandPx(cf.
[8]fordetails).
Γ∈{(1γ0)γ5,(1γ0)γj}doesnotaffecttheresultingpotentialV(r),sincethestaticquarkspinisirrelevant.
C=γ0γ2denotesthechargeconjugationmatrix.
Notethatoperatorslike(3.
2)generateoverlapnotonlytomesonicmoleculestructures,butalsotodiquark-antidiquarkstructures[15,16].
Theasymptoticvalueofapotentialandwhetheritisattractiveorrepulsivedependsonthequantumnumbers(|jz|,P,Px)and,hence,onΓ.
Inthefollowingweareexclusivelyinterestedinat-tractivepotentialsbetweentwogroundstatestatic-lightmesons:thescalarisosingletcorrespondingtoΓ=(1+γ0)γ5andthevectorisotripletcorrespondingtoΓ=(1+γ0)γj.
Computationshavebeenperformedusingtwoensemblesofgaugelinkcongurationsgener-atedbytheEuropeanTwistedMassCollaboration(ETMC)withdynamicalu/dquarks.
Informa-tionontheseensemblescanbefoundinTable1and[17,18].
βlatticesizelainfmmπinMeV#congurations3.
90243*480.
004000.
0793404804.
35323*640.
001750.
042352100Table1:Ensemblesofgaugelinkcongurations(β:inversegaugecoupling;l:bareu/dquarkmassinlatticeunits;a:latticespacing;mπ:pionmass).
4.
qqbbtetraquarksintheBorn-OppenheimerapproximationTodetermineananalyticalexpressionfortheQQpotentialorequivalentlybbpotential,wettheansatzV(r)=αrexprd2+V0(4.
1)withrespecttoα,dandV0tothelatticeQCDresultsobtainedintheprevioussection.
TheconstantV0accountsfortwicethemassofthegroundstatestatic-lightmeson.
Weinsertthetheanalyticalexpression(4.
1)intheSchrdingerequationfortheradialcoordi-nateofthetwobquarks(whichweassumetobeinans-wave),12d2dr2+U(r)R(r)=EBR(r)(4.
2)withU(r)=V(r)|V0=0and=mb/2anddeterminethelowesteigenvalueEB.
IfEB0,thereisnobinding,i.
e.
thefour-quarksystemwillalwaysbeasystemoftwounboundBmesons.
Noticethatthisso-calledBorn-Oppenheimerapproximationisvalidformqmb,whichiscertainlythecaseforq∈{u,d,s}andatleastcrudelyfullledforq=c.
Toquantifythesystematicerrorsofdifferentchannels(scalarisosingletandvectorisotriplet,differentlightavorsq∈{u,d,s,c}),weperformalargenumberoftsvaryingtherangeof3Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePeterstemporalseparationstmin≤t≤tmaxofthecorrelationfunctionC(t,r)(cf.
eq.
(3.
1)),atwhichthelatticepotentialisreadoff,aswellastherangeofspatialbbseparationsrmin≤r≤rmaxconsideredintheχ2minimizingtofeq.
(4.
1)tothelatticepotential.
Detailsonthisparametervariationcanbefoundin[2].
Foreachsetofinputparameters(tmin,tmax,rmin,rmax)wedetermineα,dandEB.
Thenwegeneratehistogramsforα,dandEBweightedaccordingtothecorrespondingχ2/dof.
Thewidthsofthesehistogramsaretakenassystematicerrorsofα,dandEB[19],whilethestatisticalerrorsareobtainedviaajackknifeanalysis.
InFigure1examplehistogramsforthescalarisosingletforqq=udareshown.
Figure1:Histogramsforthescalarisosingletforqq=ud.
Thered/green/bluebarsindicatethestatistical/systematic/combinederrors.
Theresultingpotentialstsfordifferentchannels,i.
e.
eq.
(4.
1)withcorrespondingvaluesforαandd,arecollectedinFigure2.
Theerrorbandsrepresentthecombinedsystematicandstatisticalerrors.
Onecanobservethatthepotentialsarewideranddeeperforlighterqqquarkmasses.
Moreover,thescalarchannelsaremoreattractivethantherespectivevectorchannels.
Correspondingly,itturnsoutthatthereisaboundstateonlyforthescalarisosingletwithqq=udwithbindingenergyEB=93+4743MeV,i.
e.
aboundstatewitharound2σcondencelevel.
InFigure3wepresentourresultsinanalternativegraphicalway.
Thethreeplotscorrespondtou/d,sandclightquarksqq,respectively.
Eachtofeq.
(4.
1)tolatticepotentialresultsisrepresentedbyadot(red:scalarchannels;green:vectorchannels;crosses:rmin=2a;boxes:rmin=3a).
Theextensionsofthepointcloudsrepresentthesystematicuncertaintieswithrespecttoαandd.
IfapointcloudislocalizedaboveorleftoftheisolinewithEB=0.
1MeV(essentiallythebindingthreshold),thecorrespondingfourquarksqqbbcannotformaboundstate.
Alocalizationbeloworrightofthatisolineisastrongindicationfortheexistenceofatetraquark.
Againthereisclearevidenceforatetraquarkstateinthescalaru/dchannel.
Thescalarschannelisslightlyabove,butratherclosetothebindingthreshold.
Thescalarcandallvectorchannelsclearlydonothostboundfour-quarkstates.
5.
SummaryandoutlookWehavefoundaudbbtetraquarkwithquantumnumbersI(JP)=0(1+)(i.
e.
inthescalarisosingletchannelwithqq=ud)withacondencelevelofaround2σ.
Thereseemtoexistno4Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePetersFigure2:Potentialstsfordifferentchannels(upperline:scalarisosinglet;lowerline:vectorisotriplet).
Thecurveswithoutanerrorbandarecopiedfromtherespectiveotherplotsinthesamelineforeasycomparison.
Verticallinesindicatetheavailablelatticebbseparations.
tetraquarksfortheotherchannels.
InthisworklatticeQCDcomputationshavebeenperformedforlightu/dquarkscorrespond-ingtomπ≈340MeV.
Weplantorepeattheanalysisforatleastanotherpionmassandthenextrapolatetothephysicalpoint.
Itwillthenbemostinterestingtocheck,whetheraboundstatewillalsoappearinthevectorisotripletchannelwithqq=ud.
AnotheraspectistoinvestigatethestructureofthefoundI(JP)=0(1+)tetraquark,i.
e.
toexplore,whetheritisratheramesonicmoleculeoradiquark-antidiquarkpair.
Wealsoplantoincludecorrectionsduetotheheavyquarkspins(forrstpreliminaryresultscf.
[14]).
Finally,oneshouldstudytheexperimentallymoreaccessible,buttheoreticallymorechallengingcaseofqqbbsystems.
AcknowledgmentsP.
B.
thanksIFTforhospitalityandCFTP,grantFCTUID/FIS/00777/2013,forsupport.
M.
W.
andA.
P.
acknowledgesupportbytheEmmyNoetherProgrammeoftheDFG(GermanResearchFoundation),grantWA3000/1-1.
ThisworkwassupportedinpartbytheHelmholtzInternationalCenterforFAIRwithintheframeworkoftheLOEWEprogramlaunchedbytheStateofHesse.
5Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePetersFigure3:BindingenergyisolinesEB=constantintheα-d-planeforu/d,sandclightquarksqqtogetherwiththetresultsofeq.
(4.
1)tolatticepotentials.
6Exploringpossiblyexistingqqbbtetraquarkstateswithqq=ud,ss,ccAntjePetersCalculationsontheLOEWE-CSChigh-performancecomputerofJohannWolfgangGoethe-UniversityFrankfurtamMainwereconductedforthisresearch.
WewouldliketothankHPC-Hessen,fundedbytheStateMinistryofHigherEducation,ResearchandtheArts,forprogrammingadvice.
References[1]A.
Bondaretal.
[BelleCollaboration],Phys.
Rev.
Lett.
108,122001(2012)[arXiv:1110.
2251[hep-ex]].
[2]P.
Bicudo,K.
Cichy,A.
Peters,B.
WagenbachandM.
Wagner,Phys.
Rev.
D92,014507(2015)[arXiv:1505.
00613[hep-lat]].
[3]C.
StewartandR.
Koniuk,Phys.
Rev.
D57,5581(1998)[arXiv:hep-lat/9803003].
[4]C.
MichaelandP.
Pennanen[UKQCDCollaboration],Phys.
Rev.
D60,054012(1999)[arXiv:hep-lat/9901007].
[5]M.
S.
CookandH.
R.
Fiebig,arXiv:hep-lat/0210054.
[6]T.
Doi,T.
T.
TakahashiandH.
Suganuma,AIPConf.
Proc.
842,246(2006)[arXiv:hep-lat/0601008].
[7]W.
Detmold,K.
OrginosandM.
J.
Savage,Phys.
Rev.
D76,114503(2007)[arXiv:hep-lat/0703009].
[8]M.
Wagner[ETMCollaboration],PoSLATTICE2010,162(2010)[arXiv:1008.
1538[hep-lat]].
[9]G.
BaliandM.
Hetzenegger,PoSLATTICE2010,142(2010)[arXiv:1011.
0571[hep-lat]].
[10]M.
Wagner[ETMCollaboration],ActaPhys.
Polon.
Supp.
4,747(2011)[arXiv:1103.
5147[hep-lat]].
[11]P.
BicudoandM.
Wagner,Phys.
Rev.
D87,114511(2013)[arXiv:1209.
6274[hep-ph]].
[12]Z.
S.
BrownandK.
Orginos,Phys.
Rev.
D86,114506(2012)[arXiv:1210.
1953[hep-lat]].
[13]B.
Wagenbach,P.
BicudoandM.
Wagner,J.
Phys.
Conf.
Ser.
599,012006(2015)[arXiv:1411.
2453[hep-lat]].
[14]J.
Scheunert,P.
Bicudo,A.
UenverandM.
Wagner,arXiv:1505.
03496[hep-ph].
[15]C.
Alexandrou,J.
O.
Daldrop,M.
DallaBrida,M.
Gravina,L.
Scorzato,C.
UrbachandM.
Wagner,[ETMCollaboration],JHEP1304,137(2013)[arXiv:1212.
1418].
[16]A.
Abdel-Rehim,C.
Alexandrou,J.
Berlin,M.
DallaBrida,M.
GravinaandM.
Wagner,PoSLATTICE2014,104(2014)[arXiv:1410.
8757[hep-lat]].
[17]P.
Boucaudetal.
[ETMCollaboration],Comput.
Phys.
Commun.
179,695(2008)[arXiv:0803.
0224[hep-lat]].
[18]R.
Baronetal.
[ETMCollaboration],JHEP1008,097(2010)[arXiv:0911.
5061[hep-lat]].
[19]K.
Cichy,V.
Drach,E.
Garcia-Ramos,G.
HerdoizaandK.
Jansen,Nucl.
Phys.
B869,131(2013)[arXiv:1211.
1605[hep-lat]].
7
- dominated腾讯qq好友恢复相关文档
- 支持腾讯qq好友恢复
- 胶州市民政系统信息平台(QQ群)联系表
- 引流腾讯qq好友恢复
- 腾讯qq好友恢复QQ好友如何恢复?
- 腾讯qq好友恢复QQ安全中心怎么恢复好友
HoRain Cloud:国内特价物理机服务器,镇江机房,内地5线BGP接入,月付499元起
horain怎么样?horain cloud是一家2019年成立的国人主机商家,隶属于北京辰帆科技有限公司,horain持有增值电信业务经营许可证(B1-20203595),与中国电信天翼云、腾讯云、华为云、UCloud、AWS等签署渠道合作协议,主要提企业和个人提供云服务器,目前商家推出了几款特价物理机,都是在内地,性价比不错,其中有目前性能比较强悍的AMD+NVMe系列。点击进入:horain...

hostodo:2021美国独立日7折优惠促销NVMe硬盘的VPS,低至$13/年,还送DirectAdmin授权
7月4日是美国独立日,大致就是国庆节的意思吧。hostodo今年提前搞了个VPS大促销活动,4款便宜VPS,相当于7折,续费不涨价,本次促销不定时,不知道有多少货,卖完为止。VPS基于KVM虚拟,NVMe阵列,1Gbps带宽,自带一个IPv4+/64 IPv6,solusvm管理,送收费版DirectAdmin授权,VPS在用就有效! 官方网站:https://www.hostodo.com ...
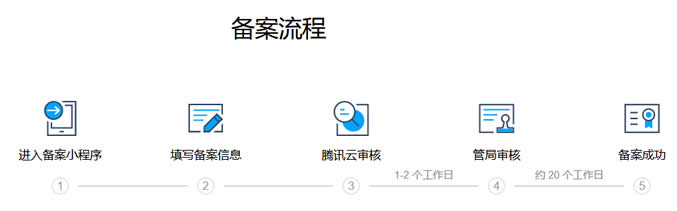
个人网站备案流程及注意事项(内容方向和适用主机商)
如今我们还有在做个人网站吗?随着自媒体和短视频的发展和兴起,包括我们很多WEB2.0产品的延续,当然也包括个人建站市场的低迷和用户关注的不同,有些个人已经不在做网站。但是,由于我们有些朋友出于网站的爱好或者说是有些项目还是基于PC端网站的,还是有网友抱有信心的,比如我们看到有一些老牌个人网站依旧在运行,且还有新网站的出现。今天在这篇文章中谈谈有网友问关于个人网站备案的问题。这个也是前几天有他在选择...
腾讯qq好友恢复为你推荐
-
竞赛winrar5关于上报下学期所需教学软件的通知大学生就业信息获取与信息分析支持ipad支持ipad支持ipad支持ipadiexplore.exe应用程序错误iexplore.exe应用程序错误css下拉菜单如何用css3做导航栏下拉菜单用itunes备份iphone怎么从itunes备份恢复