reducing63aaa.com
63aaa.com 时间:2021-04-08 阅读:()
SCIENCECHINAInformationSciencesMarch2020,Vol.
63139111:1–139111:3https://doi.
org/10.
1007/s11432-018-9495-xcScienceChinaPressandSpringer-VerlagGmbHGermany,partofSpringerNature2020info.
scichina.
comlink.
springer.
com.
LETTER.
ImproveddistinguishersearchtechniquesbasedonparitysetsXiaofengXIE&TianTIAN*NationalDigitalSwitchingSystemEngineering&TechnologicalResearchCenter,P.
O.
Box407,Zhengzhou450001,ChinaReceived12February2018/Accepted15June2018/Publishedonline10February2020CitationXieXF,TianT.
Improveddistinguishersearchtechniquesbasedonparitysets.
SciChinaInfSci,2020,63(3):139111,https://doi.
org/10.
1007/s11432-018-9495-xDeareditor,DivisionpropertywasatechniqueproposedbyTodoatEUROCRYPT2015tosearchintegraldis-tinguishersagainstblockciphers[1].
Todo[2]ap-pliedthistechniquetoperformstructuralevalu-ationagainstboththeFeistelandtheSPNcon-structionsandattackedthefullMISTY1.
Sub-sequently,manyimprovedtechniquesbasedonthedivisionpropertywereproposed[3,4].
AtFSE2016,TodoandMorii[3]introducedthebit-baseddivisionpropertyandproveditseective-nesstonddistinguishersagainstnon-S-box-basedciphers.
Althoughmoreaccurateintegraldistinguisherswerefoundbyusingthebit-baseddivisionprop-erty,itcouldnotbeappliedtocipherswhoseblocklengthismorethan32becauseofitshightimeandmemorycomplexities.
BasedonTodo'swork,Xiangetal.
[5]convertedthedistinguishersearchalgorithmbasedonthebit-baseddivisionpropertyintoanMILPproblematASIACRYPT2016.
Withthismethod,theyobtainedaseriesofimprovedresultsincludinga9-roundPRESENTdistinguisherwithonebalancedbit.
Thisdistin-guisherisoneofthebest-knowndistinguishersre-latedtoroundnumbers.
AtCRYPTO2016,BouraandCauteaut[6]introducedtheparitysettostudythedivi-sionproperty.
TheyutilizedtheparitysettoexploitfurtherpropertiesofthePRESENTS-boxandthePRESENTlinearlayer,leadingtoseveralimproveddistinguishersagainstreduced-roundPRESENT.
BecausemorepropertiesoftheS-boxandthelinearlayerareutilized,paritysetscanndmoreaccurateintegralcharacteris-tics.
However,althoughtheauthorsdidnotpointout,aparitysetrequireshighertimeandmemorycomplexitiesthanthedivisionpropertydoes.
Ourworkaimsatreducingtimeandmemorycomplex-itieswhenusingparitysetstosearchintegraldis-tinguishers.
Asaresult,weintroducetheideaofmeet-in-the-middleintothedistinguishersearch.
Toillustrateourtechniques,weperformedexten-siveexperimentsonPRESENTandfounda9-rounddistinguisherwith22balancedbits.
Notation1(Bitproductfunction).
Letu,x∈Fn2.
Denotexu=ni=1x[i]u[i],andforu,x∈Fn12*Fn22Fnm2,wherex=(x1,x2,xm),u=(u1,u2,um),denebitproductfunctionasxu=mi=1xuii.
Notation2(Comparisonbetweenvectors).
Fora,b∈Zm,denoteabifaibiforall0bifabbuta=b.
Foru∈Fn2,letusdenotePrec(u)={v∈Fn2:vu},Succ(u)={v∈Fn2:uv}.
*Correspondingauthor(email:tiantiand@126.
com)XieXF,etal.
SciChinaInfSciMarch2020Vol.
63139111:2Theorem1.
Ifu,v∈Fnt2satisfyuv,thenW(u)W(v).
Notation3(Comparisonbetweensets).
LetAandBbetwosetswhoseelementsareinFn2.
De-noteABifthereexista∈Aandb∈Bwithab,andABifnoneofsuchcoupleexists.
Proposition1.
LetAandBbetwosetswhoseelementsareinFn2withAB.
Iftherearea1,a2∈A,b1,b2∈Bsuchthata2a1andb1b2,thenA\{a1}B\{b1}.
Notation4(Roundfunction).
LetFbeaper-mutationofFn2denedbyF:x=(x1,x2,xn)→y=(y1,y2,yn).
TheneveryyicanbeseenasaBooleanfunctiononx1,x2,xn,denotedbyyi=Fi(x).
Forapositiveintegerr,wedenoteFrasacompositionofrpermutationF.
Denition1(Divisionproperty[1]).
LetXbeamultisetwhoseelementsbelongtoFn2.
Then,XhasthedivisionpropertyDnkwhenitfulllsthefollowingconditions:Foru∈Fn2,theparityofxuoverallelementsinXisalwaysevenwhenwt(u)Forfurtherstudyofthedivisionprop-erty,pleasereferto[1,4]indetail.
Denition2(Parityset[6]).
LetXbeasetwhoseelementstakevaluesofFn2.
TheparitysetofXisdenotedbyU(X)anddenedasfollows:U(X)=u∈Fn2:x∈Xxu=1.
Remark1.
IftheparitysetU(X)ofXisknown,thenthedivisionpropertyofXisgivenbyDnk,wherek=minu∈U(X)wt(u).
ForthepropagationrulesoftheparitysetonSPN,pleasereferto[1].
ForaninputsetXandaroundfunctionE,de-notetheparitysetafterr1-roundencryptionasU(Er1(X)),andthealgebraicnormalform(ANF)ofthei-thoutputbitafterr2-roundencryptionasEr2i(x).
IfallthetermsappearinginEr2i(x)arenotdivisiblebyanytermin{xu:u∈U(Er(X))},thenthei-thoutputbitof(r1+r2)-roundencryp-tionisbalanced.
Basedonthisobservation,weimprovedthein-tegraldistinguishersearchbyutilizingthemeet-in-the-middletechniquewhichdividesthen-roundpropagationofparitysetsinton1-roundpropaga-tionofparitysetsand(nn1)-roundpropagationoftheANF.
Next,weproposeanewconcept,whichwecalltermset,todescribetheANFandshowtheprop-agationrulesofthetermsetonSPN.
Denition3(Termset).
Letf(x)beann-variableBooleanfunction.
Thetermsetoff(x)denotedbyT(f)isthesubsetofFn2denedbyT(f)={u∈Fn2:xuappearsintheANFoff(x)}.
Proposition2.
LetSbeanS-boxoverFm2.
De-noteTs(u)={v∈Fm2:xvappearsintheANFofSu(x)}.
Thenforanm-variableBooleanfunctionfwiththetermsetT(f),wehaveT(f(S(x)))u∈T(f)Ts(u).
Proposition3.
LetSbeapermutationofFmt2whichconsistsoftparallelindepen-dentS-boxesoverFm2,namely,S(x1,xt)=(S(x1)S(xt)).
Foranmt-variableBooleanfunctionfwiththetermsetT(f),wehaveT(f(S))(u1,···,ut)∈T(f)Ts1(u1)Tst(ut).
Proposition4.
Letfbeann-variableBooleanfunctionwiththetermsetT(f).
Foranyk∈Fn2,thetermsetoff(kx)=(x1k1,xnkn)satisesT(f(kx))u∈T(f)Prec(u).
Then,thetermsetafteroneroundencryptioncanbededucedbyPropositions2and4,i.
e.
,T(f(S(xk)))u∈T(f)v∈Ts(u)Prec(v),fork∈Fn2.
Theproofsofthesepropositionscouldbefoundthroughhttps://eprint.
iacr.
org/2018/447.
Wecanalsosearchdistinguishersbytermsetsonly.
Ifthereexistsau∈Fn2satisfyingSucc(u)T(Eri)=,thenar-rounddistinguisherwhoseinputsetisPrec(u)isfound.
However,thetimeandmemorycomplexitieswillbeveryhigh.
Thus,wetookadvantageofthemeet-in-the-middletechniquesothatthetermsetandtheparitysetcouldbecombinedtoreducetimeandmemorycomplexities.
Inordertondadistinguisher,weneedtocom-pareT(Er2i)withU(Er1(X))andverifywhetherT(Er2i)U(Er1(X)).
Ourdistinguishersearchalgorithmconsistsofvesteps,whichcanbede-scribedasfollows.
XieXF,etal.
SciChinaInfSciMarch2020Vol.
63139111:3Step1.
Choosethepropagationroundnum-bersr1andr2fortheparitysetandthetermsetrespectively,wherer1+r2=r.
Step2.
ChooseaninputsetX.
Step3.
CalculatetheparitysetU(Er1(X)).
Step4.
CalculatethetermsetsT(Er2i)for1in.
Step5.
CompareU(Er1(X))withT(Er2i)for1in.
IfU(Er1(X))T(Er2i),thenthei-thoutputbitinr-roundencryptionisbalanced.
Ifnoneofsuchintersectionsisempty,thenchooseanotherXandgotoStep2.
Wealsoproposesomenoveltechniquestomakeouralgorithmmoreecient.
Sizereduceoperation.
ForthetermsetT(Eri(x)),thesizereduceoperationRtremovesalltheelementsv∈T(Eri(x))suchthatthereisanelementv′∈T(Eri(x))withv′v.
Asforaparityset,theoperationRuremovesalltheelementsu∈U(Er1(X))suchthatthereisanelementu′∈U(Er1(X))withuu′.
ItcanbededucedfromProposition1thatthecom-parisonresultofT(Eri(x))andU(Er1(X))isthesameasthecomparisonresultofRt(T(Eri(x)))andRu(U(Er1(X))).
Observation1.
ThePRESENTsuperS-boxescanworkindependentlyinthe2-roundencryption.
Reducinglook-uptable.
BasedonObserva-tion1,wecaneasilyconstructa2-roundpropaga-tiontableforthesuperS-boxbycalculatingRuU(S(P(S(X))))forallpossibleinputs,whereSisapermutationofF4n2consistingoffourPRESENTS-boxesS(x1,x2,x3,x4)=(S(x1),S(x2),S(x3),S(x4)).
Multiplecomparison.
Thistechniqueat-temptstoremovethetermsthathavenomultipleinU;ifnotermisdivisiblebyavectorinU,thenitisclearthattheoutputbitisbalanced.
Wetriedtojudgesuchdivisibilityintermsofdegreeorderandalphabetorder.
Forthedetailsofthistech-nique,refertohttps://eprint.
iacr.
org/2018/447.
Toillustrateourtechniques,weapplyouralgo-rithmtothePRESENTdistinguishersearch.
Observation2.
ThecubictermsintheANFsofthesecondandfourthcoordinatesofthePRESENTS-box(sayS2andS4)arethesame[7].
Asaresult,thexorofthesetwocoordinatesS2S4=1x1x2x3x2x4x3x4hasonlydegree2.
Moreover,everyterminS2S4hasamultipleinS2andS4respectively.
Hence,S2S4maybebalancedevenifS2andS4areunbalanced.
Wetriedtond10-roundPRESENTdistin-guishersrst,buttheresultoftherightmostout-putbitisunbalancedforalltheinputsetswithdimension63.
ItseemsthattheANFofthisout-putbitisthesimplestamong64outputbits,andtherefore,ourresultsshowthatthePRESENTprobablyhasno10-roundintegraldistinguishersbyonlyusingthedivisionproperty.
Then,wefo-cusonthe9-roundPRESENT,andndadistin-guisherwith22balancedoutputbits.
Input:(aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaac),Output:b3b3bb2b2bb1b1bbbbbbbbbbbbbbbbb),where"c"meansaconstantbit,"a"meansanac-tivebit,""meansanunknownbit,and"b"meansabalancedbit.
Inaddition,thepresenceofbitswiththesamenotationbimeanstheiradditionisbalanced.
Conclusion.
Inthisstudy,weproposedacon-ceptcalledthetermsettopropagateinformationoftheANF.
Withtermsets,weimprovedthedis-tinguishersearchmethodbasedontheparitysetintermsofbothmemoryandtimecomplexities.
Fromtherelationbetweentheparitysetandthebit-baseddivisionproperty,itwasfoundthatthetermsetcouldalsobeappliedtoimprovethedis-tinguishersearchmethodbasedonthebit-baseddivisionproperty.
AcknowledgementsThisworkwassupportedbyNa-tionalNaturalScienceFoundationofChina(GrantNo.
61672533).
References1TodoY.
Structuralevaluationbygeneralizedintegralproperty.
LectNotesComputSci,2015,9056:287–3142TodoY.
IntegralcryptanalysisonfullMISTY1.
JCryptol,2017,30:920–9593TodoY,MoriiM.
Bit-baseddivisionpropertyandap-plicationtosimonfamily.
LectNotesComputSci,2016,9783:357–3774SunL,WangW,WangMQ.
Automaticsearchofbit-baseddivisionpropertyforARXciphersandword-baseddivisionproperty.
LectNotesComputSci,2017,10624:128–1575XiangZJ,ZhangWT,BaoZZ,etal.
ApplyingMILPmethodtosearchingintegraldistinguishersbasedondivisionpropertyfor6lightweightblockciphers.
LectNotesComputSci,2016,10031:648–6786BouraC,CanteautA.
Anotherviewofthedivisionproperty.
LectNotesComputSci,2016,9814:654–6827BogdanovA,KnudsenLR,LeanderG,etal.
PRESENT:anultra-lightweightblockcipher.
LectNotesComputSci,2007,4727:450–466
63139111:1–139111:3https://doi.
org/10.
1007/s11432-018-9495-xcScienceChinaPressandSpringer-VerlagGmbHGermany,partofSpringerNature2020info.
scichina.
comlink.
springer.
com.
LETTER.
ImproveddistinguishersearchtechniquesbasedonparitysetsXiaofengXIE&TianTIAN*NationalDigitalSwitchingSystemEngineering&TechnologicalResearchCenter,P.
O.
Box407,Zhengzhou450001,ChinaReceived12February2018/Accepted15June2018/Publishedonline10February2020CitationXieXF,TianT.
Improveddistinguishersearchtechniquesbasedonparitysets.
SciChinaInfSci,2020,63(3):139111,https://doi.
org/10.
1007/s11432-018-9495-xDeareditor,DivisionpropertywasatechniqueproposedbyTodoatEUROCRYPT2015tosearchintegraldis-tinguishersagainstblockciphers[1].
Todo[2]ap-pliedthistechniquetoperformstructuralevalu-ationagainstboththeFeistelandtheSPNcon-structionsandattackedthefullMISTY1.
Sub-sequently,manyimprovedtechniquesbasedonthedivisionpropertywereproposed[3,4].
AtFSE2016,TodoandMorii[3]introducedthebit-baseddivisionpropertyandproveditseective-nesstonddistinguishersagainstnon-S-box-basedciphers.
Althoughmoreaccurateintegraldistinguisherswerefoundbyusingthebit-baseddivisionprop-erty,itcouldnotbeappliedtocipherswhoseblocklengthismorethan32becauseofitshightimeandmemorycomplexities.
BasedonTodo'swork,Xiangetal.
[5]convertedthedistinguishersearchalgorithmbasedonthebit-baseddivisionpropertyintoanMILPproblematASIACRYPT2016.
Withthismethod,theyobtainedaseriesofimprovedresultsincludinga9-roundPRESENTdistinguisherwithonebalancedbit.
Thisdistin-guisherisoneofthebest-knowndistinguishersre-latedtoroundnumbers.
AtCRYPTO2016,BouraandCauteaut[6]introducedtheparitysettostudythedivi-sionproperty.
TheyutilizedtheparitysettoexploitfurtherpropertiesofthePRESENTS-boxandthePRESENTlinearlayer,leadingtoseveralimproveddistinguishersagainstreduced-roundPRESENT.
BecausemorepropertiesoftheS-boxandthelinearlayerareutilized,paritysetscanndmoreaccurateintegralcharacteris-tics.
However,althoughtheauthorsdidnotpointout,aparitysetrequireshighertimeandmemorycomplexitiesthanthedivisionpropertydoes.
Ourworkaimsatreducingtimeandmemorycomplex-itieswhenusingparitysetstosearchintegraldis-tinguishers.
Asaresult,weintroducetheideaofmeet-in-the-middleintothedistinguishersearch.
Toillustrateourtechniques,weperformedexten-siveexperimentsonPRESENTandfounda9-rounddistinguisherwith22balancedbits.
Notation1(Bitproductfunction).
Letu,x∈Fn2.
Denotexu=ni=1x[i]u[i],andforu,x∈Fn12*Fn22Fnm2,wherex=(x1,x2,xm),u=(u1,u2,um),denebitproductfunctionasxu=mi=1xuii.
Notation2(Comparisonbetweenvectors).
Fora,b∈Zm,denoteabifaibiforall0bifabbuta=b.
Foru∈Fn2,letusdenotePrec(u)={v∈Fn2:vu},Succ(u)={v∈Fn2:uv}.
*Correspondingauthor(email:tiantiand@126.
com)XieXF,etal.
SciChinaInfSciMarch2020Vol.
63139111:2Theorem1.
Ifu,v∈Fnt2satisfyuv,thenW(u)W(v).
Notation3(Comparisonbetweensets).
LetAandBbetwosetswhoseelementsareinFn2.
De-noteABifthereexista∈Aandb∈Bwithab,andABifnoneofsuchcoupleexists.
Proposition1.
LetAandBbetwosetswhoseelementsareinFn2withAB.
Iftherearea1,a2∈A,b1,b2∈Bsuchthata2a1andb1b2,thenA\{a1}B\{b1}.
Notation4(Roundfunction).
LetFbeaper-mutationofFn2denedbyF:x=(x1,x2,xn)→y=(y1,y2,yn).
TheneveryyicanbeseenasaBooleanfunctiononx1,x2,xn,denotedbyyi=Fi(x).
Forapositiveintegerr,wedenoteFrasacompositionofrpermutationF.
Denition1(Divisionproperty[1]).
LetXbeamultisetwhoseelementsbelongtoFn2.
Then,XhasthedivisionpropertyDnkwhenitfulllsthefollowingconditions:Foru∈Fn2,theparityofxuoverallelementsinXisalwaysevenwhenwt(u)
Denition2(Parityset[6]).
LetXbeasetwhoseelementstakevaluesofFn2.
TheparitysetofXisdenotedbyU(X)anddenedasfollows:U(X)=u∈Fn2:x∈Xxu=1.
Remark1.
IftheparitysetU(X)ofXisknown,thenthedivisionpropertyofXisgivenbyDnk,wherek=minu∈U(X)wt(u).
ForthepropagationrulesoftheparitysetonSPN,pleasereferto[1].
ForaninputsetXandaroundfunctionE,de-notetheparitysetafterr1-roundencryptionasU(Er1(X)),andthealgebraicnormalform(ANF)ofthei-thoutputbitafterr2-roundencryptionasEr2i(x).
IfallthetermsappearinginEr2i(x)arenotdivisiblebyanytermin{xu:u∈U(Er(X))},thenthei-thoutputbitof(r1+r2)-roundencryp-tionisbalanced.
Basedonthisobservation,weimprovedthein-tegraldistinguishersearchbyutilizingthemeet-in-the-middletechniquewhichdividesthen-roundpropagationofparitysetsinton1-roundpropaga-tionofparitysetsand(nn1)-roundpropagationoftheANF.
Next,weproposeanewconcept,whichwecalltermset,todescribetheANFandshowtheprop-agationrulesofthetermsetonSPN.
Denition3(Termset).
Letf(x)beann-variableBooleanfunction.
Thetermsetoff(x)denotedbyT(f)isthesubsetofFn2denedbyT(f)={u∈Fn2:xuappearsintheANFoff(x)}.
Proposition2.
LetSbeanS-boxoverFm2.
De-noteTs(u)={v∈Fm2:xvappearsintheANFofSu(x)}.
Thenforanm-variableBooleanfunctionfwiththetermsetT(f),wehaveT(f(S(x)))u∈T(f)Ts(u).
Proposition3.
LetSbeapermutationofFmt2whichconsistsoftparallelindepen-dentS-boxesoverFm2,namely,S(x1,xt)=(S(x1)S(xt)).
Foranmt-variableBooleanfunctionfwiththetermsetT(f),wehaveT(f(S))(u1,···,ut)∈T(f)Ts1(u1)Tst(ut).
Proposition4.
Letfbeann-variableBooleanfunctionwiththetermsetT(f).
Foranyk∈Fn2,thetermsetoff(kx)=(x1k1,xnkn)satisesT(f(kx))u∈T(f)Prec(u).
Then,thetermsetafteroneroundencryptioncanbededucedbyPropositions2and4,i.
e.
,T(f(S(xk)))u∈T(f)v∈Ts(u)Prec(v),fork∈Fn2.
Theproofsofthesepropositionscouldbefoundthroughhttps://eprint.
iacr.
org/2018/447.
Wecanalsosearchdistinguishersbytermsetsonly.
Ifthereexistsau∈Fn2satisfyingSucc(u)T(Eri)=,thenar-rounddistinguisherwhoseinputsetisPrec(u)isfound.
However,thetimeandmemorycomplexitieswillbeveryhigh.
Thus,wetookadvantageofthemeet-in-the-middletechniquesothatthetermsetandtheparitysetcouldbecombinedtoreducetimeandmemorycomplexities.
Inordertondadistinguisher,weneedtocom-pareT(Er2i)withU(Er1(X))andverifywhetherT(Er2i)U(Er1(X)).
Ourdistinguishersearchalgorithmconsistsofvesteps,whichcanbede-scribedasfollows.
XieXF,etal.
SciChinaInfSciMarch2020Vol.
63139111:3Step1.
Choosethepropagationroundnum-bersr1andr2fortheparitysetandthetermsetrespectively,wherer1+r2=r.
Step2.
ChooseaninputsetX.
Step3.
CalculatetheparitysetU(Er1(X)).
Step4.
CalculatethetermsetsT(Er2i)for1in.
Step5.
CompareU(Er1(X))withT(Er2i)for1in.
IfU(Er1(X))T(Er2i),thenthei-thoutputbitinr-roundencryptionisbalanced.
Ifnoneofsuchintersectionsisempty,thenchooseanotherXandgotoStep2.
Wealsoproposesomenoveltechniquestomakeouralgorithmmoreecient.
Sizereduceoperation.
ForthetermsetT(Eri(x)),thesizereduceoperationRtremovesalltheelementsv∈T(Eri(x))suchthatthereisanelementv′∈T(Eri(x))withv′v.
Asforaparityset,theoperationRuremovesalltheelementsu∈U(Er1(X))suchthatthereisanelementu′∈U(Er1(X))withuu′.
ItcanbededucedfromProposition1thatthecom-parisonresultofT(Eri(x))andU(Er1(X))isthesameasthecomparisonresultofRt(T(Eri(x)))andRu(U(Er1(X))).
Observation1.
ThePRESENTsuperS-boxescanworkindependentlyinthe2-roundencryption.
Reducinglook-uptable.
BasedonObserva-tion1,wecaneasilyconstructa2-roundpropaga-tiontableforthesuperS-boxbycalculatingRuU(S(P(S(X))))forallpossibleinputs,whereSisapermutationofF4n2consistingoffourPRESENTS-boxesS(x1,x2,x3,x4)=(S(x1),S(x2),S(x3),S(x4)).
Multiplecomparison.
Thistechniqueat-temptstoremovethetermsthathavenomultipleinU;ifnotermisdivisiblebyavectorinU,thenitisclearthattheoutputbitisbalanced.
Wetriedtojudgesuchdivisibilityintermsofdegreeorderandalphabetorder.
Forthedetailsofthistech-nique,refertohttps://eprint.
iacr.
org/2018/447.
Toillustrateourtechniques,weapplyouralgo-rithmtothePRESENTdistinguishersearch.
Observation2.
ThecubictermsintheANFsofthesecondandfourthcoordinatesofthePRESENTS-box(sayS2andS4)arethesame[7].
Asaresult,thexorofthesetwocoordinatesS2S4=1x1x2x3x2x4x3x4hasonlydegree2.
Moreover,everyterminS2S4hasamultipleinS2andS4respectively.
Hence,S2S4maybebalancedevenifS2andS4areunbalanced.
Wetriedtond10-roundPRESENTdistin-guishersrst,buttheresultoftherightmostout-putbitisunbalancedforalltheinputsetswithdimension63.
ItseemsthattheANFofthisout-putbitisthesimplestamong64outputbits,andtherefore,ourresultsshowthatthePRESENTprobablyhasno10-roundintegraldistinguishersbyonlyusingthedivisionproperty.
Then,wefo-cusonthe9-roundPRESENT,andndadistin-guisherwith22balancedoutputbits.
Input:(aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaac),Output:b3b3bb2b2bb1b1bbbbbbbbbbbbbbbbb),where"c"meansaconstantbit,"a"meansanac-tivebit,""meansanunknownbit,and"b"meansabalancedbit.
Inaddition,thepresenceofbitswiththesamenotationbimeanstheiradditionisbalanced.
Conclusion.
Inthisstudy,weproposedacon-ceptcalledthetermsettopropagateinformationoftheANF.
Withtermsets,weimprovedthedis-tinguishersearchmethodbasedontheparitysetintermsofbothmemoryandtimecomplexities.
Fromtherelationbetweentheparitysetandthebit-baseddivisionproperty,itwasfoundthatthetermsetcouldalsobeappliedtoimprovethedis-tinguishersearchmethodbasedonthebit-baseddivisionproperty.
AcknowledgementsThisworkwassupportedbyNa-tionalNaturalScienceFoundationofChina(GrantNo.
61672533).
References1TodoY.
Structuralevaluationbygeneralizedintegralproperty.
LectNotesComputSci,2015,9056:287–3142TodoY.
IntegralcryptanalysisonfullMISTY1.
JCryptol,2017,30:920–9593TodoY,MoriiM.
Bit-baseddivisionpropertyandap-plicationtosimonfamily.
LectNotesComputSci,2016,9783:357–3774SunL,WangW,WangMQ.
Automaticsearchofbit-baseddivisionpropertyforARXciphersandword-baseddivisionproperty.
LectNotesComputSci,2017,10624:128–1575XiangZJ,ZhangWT,BaoZZ,etal.
ApplyingMILPmethodtosearchingintegraldistinguishersbasedondivisionpropertyfor6lightweightblockciphers.
LectNotesComputSci,2016,10031:648–6786BouraC,CanteautA.
Anotherviewofthedivisionproperty.
LectNotesComputSci,2016,9814:654–6827BogdanovA,KnudsenLR,LeanderG,etal.
PRESENT:anultra-lightweightblockcipher.
LectNotesComputSci,2007,4727:450–466
- reducing63aaa.com相关文档
- analyser63aaa.com
- 请务必阅读正文之后的信息披露和法律声明
- 广安63aaa.com
- voltages63aaa.com
- organized63aaa.com
- C663aaa.com
HTTPS加密协议端口默认是多少且是否支持更换端口访问
看到群里网友们在讨论由于不清楚的原因,有同学的网站无法访问。他的网站是没有用HTTPS的,直接访问他的HTTP是无法访问的,通过PING测试可以看到解析地址已经比较乱,应该是所谓的DNS污染。其中有网友提到采用HTTPS加密证书试试。因为HTTP和HTTPS走的不是一个端口,之前有网友这样测试过是可以缓解这样的问题。这样通过将网站绑定设置HTTPS之后,是可以打开的,看来网站的80端口出现问题,而...

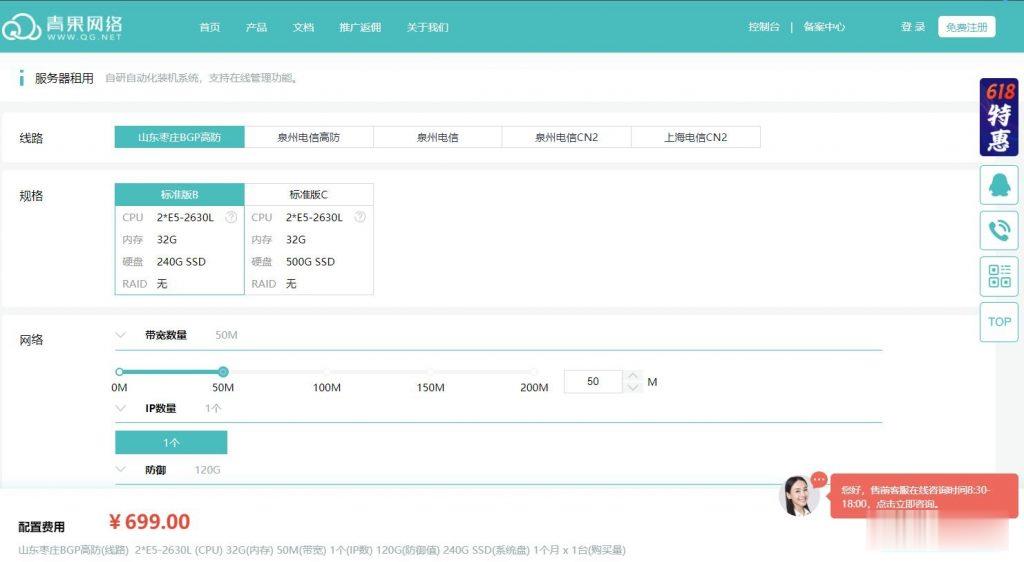
青果网络-618阿里云,腾讯云特惠优惠折上折!
官方网站:点击访问青果云官方网站活动方案:—————————–活动规则—————————1、选购活动产品并下单(先不要支付)2、联系我司在线客服修改价格或领取赠送时间3、确认价格已按活动政策修改正确后,支付订单,到此产品开设成功4、本活动产品可以升级,升级所需费用按产品原价计算若发生退款,按资源实际使用情况折算为产品原价再退还剩余余额! 美国洛杉矶CN2_GIACPU内存系统盘流量宽带i...
Gigsgigscloud($9.8)联通用户优选日本软银VPS
gigsgigsCloud日本东京软银VPS的大带宽配置有100Mbps、150Mbps和200Mbps三种,三网都走软银直连,售价最低9.8美元/月、年付98美元。gigsgigscloud带宽较大延迟低,联通用户的好选择!Gigsgigscloud 日本软银(BBTEC, SoftBank)线路,在速度/延迟/价格方面,是目前联通用户海外VPS的最佳选择,与美国VPS想比,日本软银VPS延迟更...
63aaa.com为你推荐
-
存储备份数据备份有哪些方式呢?急救知识纳入考试急救证容易拿到么?h连锁酒店连锁酒店有哪些地图应用谁知道什么地图软件好用,求 最好可以看到路上行人百度关键词价格查询百度竞价关键词价格查询,帮忙查几个词儿点击一次多少钱,thankspsbc.com95580是什么诈骗信息不点网址就安全吧!8090lu.com8090看看电影网怎么打不开了mole.61.com摩尔庄园RK的秘密是什么?www.zjs.com.cn我的信用卡已经申请成功了,显示正在寄卡,怎么查询寄卡信息?抓站工具大家在家用什么工具练站?怎么固定?面壁思过?在医院是站站立架