adds66456.com
66456.com 时间:2021-04-06 阅读:()
MarceloR.
EbertMichaelReissigMethodsforPartialDifferentialEquationsQualitativePropertiesofSolutions,PhaseSpaceAnalysis,SemilinearModelsMarceloR.
EbertUniversityofSQaoPauloDepartmentofComputingandMathematicsRibeiroPreto,SoPaulo,BrazilMichaelReissigTUBergakademieFreibergInstituteofAppliedAnalysisFreiberg,GermanyISBN978-3-319-66455-2ISBN978-3-319-66456-9(eBook)https://doi.
org/10.
1007/978-3-319-66456-9LibraryofCongressControlNumber:2017963017MathematicsSubjectClassication(2010):35-01,35-02,35A01,35A02,35A10,35B30,35B33,35B40,35B44,35E20,35F20,35F35,35J05,35J10,35J99,35K05,35K99,35L05,35L45,35L71,35L99SpringerInternationalPublishingAG2018Thisworkissubjecttocopyright.
AllrightsarereservedbythePublisher,whetherthewholeorpartofthematerialisconcerned,specicallytherightsoftranslation,reprinting,reuseofillustrations,recitation,broadcasting,reproductiononmicrolmsorinanyotherphysicalway,andtransmissionorinformationstorageandretrieval,electronicadaptation,computersoftware,orbysimilarordissimilarmethodologynowknownorhereafterdeveloped.
Theuseofgeneraldescriptivenames,registerednames,trademarks,servicemarks,etc.
inthispublicationdoesnotimply,evenintheabsenceofaspecicstatement,thatsuchnamesareexemptfromtherelevantprotectivelawsandregulationsandthereforefreeforgeneraluse.
Thepublisher,theauthorsandtheeditorsaresafetoassumethattheadviceandinformationinthisbookarebelievedtobetrueandaccurateatthedateofpublication.
Neitherthepublishernortheauthorsortheeditorsgiveawarranty,expressorimplied,withrespecttothematerialcontainedhereinorforanyerrorsoromissionsthatmayhavebeenmade.
Thepublisherremainsneutralwithregardtojurisdictionalclaimsinpublishedmapsandinstitutionalafliations.
Printedonacid-freepaperThisbookispublishedunderthetradenameBirkhuser,www.
birkhauser-science.
comTheregisteredcompanyisSpringerInternationalPublishingAGTheregisteredcompanyaddressis:Gewerbestrasse11,6330Cham,SwitzerlandDedicatedtoourwivesHelenaandStefPrefaceItistheaimofthisbooktomotivateyoungmathematiciansatthepostgraduateleveltostartstudyingdifferenttopicsofthetheoryofpartialdifferentialequations.
ThebookisaddressedtoMasterandPhDstudentswithinterestinthistheory.
AfterattendingintroductorycoursesonPDE's,usuallyattheendofundergraduatestudies,thebackgroundsofthosestudentsmayvarywidely.
SometimesthetheoryonPDE'sisreducedtoFourier'smethodandintegraltransformationsonly.
ThemainpurposeofthisbookistoamplifyanadvancedcourseonPDE'sduringgraduatestudies.
Thebookprovidesanoverviewondifferenttopicsofthetheoryofpartialdifferentialequations.
Asitisannouncedinthetitle,theexplanationofqualitativepropertiesofsolutionsoflinearmodels,theintroductiontophasespaceanalysisontheonehandandmodernmethodshowtotreatsemilinearmodelsontheotherhand,formthecoreofthebook.
TheauthorshavechosenthesesubtitlesbecauseadeeperknowledgeofthesetopicsisanimportantbasefromwhichtoapplyordevelopthetheoryofPDE's.
Usually,introductorycoursesonPDE'scontainonlyveryfewpropertiesofsolutionstobasicPDE's.
WewillillustratequalitativepropertiesofsolutionsofmodelequationsshowingfundamentaldifferencesbetweenpropertiesofsolutionstoLaplace,heat,waveorSchrdingerequations.
Adeepknowledgeofsuchprop-ertieshelpsinunderstandingtheapplicabilityofdifferentmethodsortechniquestotreatmorecomplexmodels.
PhasespaceanalysisiswidelyappliedinalotofbranchesofthetheoryofPDE's.
OnlyaverycarefuldescriptionofFouriertransformoffunctionsorevendistributionstogetherwithdecompositiontechniquesofthephasespaceallowsforattackingalotofproblemsfromthetheoryofpartialdifferentialequations.
WithouthavingtoolsfromWKBanalysis,thetheoryofpseudo-differentialorpara-differentialoperators,alotofmodelscannotbetreatedinanoptimalway.
Forthisreasontheauthorsincludedchaptersonbasicsofphasespaceanalysis.
Themovefromlinearmodelstononlinearonesisabigchallenge.
Evenifoneaddsthemostsimplenonlinearitiesjujpor˙jujp1uasanonlinearright-handsideinalinearmodelitcausesalotofnewdifculties.
Sometimessuchatermdeterminesnewtrendsinthetheory.
Theauthorsshowbysemilinearheat,waveorSchrdingerviiviiiPrefacemodelsthebiginuenceofthesenonlinearitiesonmethods,trendsandexpectedresults.
Adeepknowledgeofhowtotreatsemilinearmodelssimpliesthemovetounderstandquasi-ornonlinearmodelsaswell.
TheauthorshaveyearsofexperiencegivingcoursesonPDE'satundergraduateandgraduatelevelandsupervisingPhDstudents.
Thebookcontainstheircombinedteachingandsupervisingexpertise.
Thecourseswereheldatvariousuniversitiesthroughouttheworld.
In2009,therstauthorgaveacourseabouttheCauchyproblemforpartialdifferentialoperatorswithinthe27thBrazilianMathematicsColloquiumatInstitutoNacionaldeMatemáticaPuraeAplicada(IMPA)inRiodeJaneiro.
UpontheinvitationofProf.
SandraLucente,thesecondauthorstayedattheUniversityofBariinItalyduringNovember2013,andgaveaseriesoflecturesonpartialdifferentialequationswithinthe"ProjectMessaggeridellaConoscenza2012,ID424",supportedbythegovernmentofItaly.
TheaudiencewascomposedofMasterandPhDstudentsnotonlyfromUniversityofBari.
Thiscomprehensivecoursewasonlyoneofaseriesofninecourseson"BasicsofPartialDifferentialEquations"thesecondauthorgaveduringtheperiod2007–2016attheShanghaiJiao-TongUniversity,KazakhNationalUniversityAlFarabyAlma-AtyinKaza-khstan,theEurasianNationalUniversityL.
N.
GumilevaAstanainKazakhstan,theHanoiNationalUniversityofEducationandtheHanoiUniversityofScienceandTechnologyinVietnam.
Thesecondauthorsince2002givesthecourse"PartialDifferentialEquations1/2"attheFacultyforMathematicsandComputerScienceofTechnicalUniversityBergakademieFreiberg,andherehesupervised15PhDstudents,severalofthemfromabroad.
TherstauthorspenttheperiodJuly2014–July2015,hissabbaticalyear,inFreiberg.
Duringthistimehegaveadvancedseminarson"PartialDifferentialEquations"forMasterstudents.
Fromallactivitiesarosethejointideatowritethisbook.
Itwillbeourgreatpleasureshouldthisbookstimulateyoungmathematicianstobecomefamiliarwiththebeautifultheoryofpartialdifferentialequations.
RibeiroPreto,SoPaulo,BrazilMarceloR.
EbertFreiberg,GermanyMichaelReissigJune2017AcknowledgementsTheideatowritethisbookaroseduringthestayoftherstauthor(July2014–July2015)attheInstituteofAppliedAnalysisatTUBergakademieFreiberg.
ThestayoftherstauthorwassupportedbyFundaodeAmparoàPesquisadoEstadodeSoPaulo(FAPESP),grant2013/20297-8.
ThebookwascompletedwithintheDFGprojectRE961/21-1andFAPESPGrant2015/16038-2.
TheauthorsthankVladimirGeorgiev,SandraLucente,WinfriedSickel,MitsuruSugimoto,HiroyukiTakamuraandKarenYagdjianforfruitfuldiscussionsonthecontentofsomepartsofthisbook.
Moreover,theauthorsthankformerPhDstudentsAbdelhamidMohammedDjaouti,ChristianJh,WanderleyNunesdoNascimento,AlessandroPalmieriandMaximilianReichforreadingsomeofthechapters.
Finally,wethankthestafffromBirkhuserpublishinghouse,inparticular,SarahGoobandDr.
ThomasHemping,forthefruitfulco-operationinpreparingthenalversionofthisbook.
ixContentsPartI1Introduction32PartialDifferentialEquationsinModels72.
1AGeneralConservationLaw.
72.
2TransportorConvection82.
3Diffusion92.
4StationaryModels.
102.
5WavesinAcoustics112.
6QuantumMechanics132.
7Gas-andHydrodynamics.
142.
8ConcludingRemarks.
143BasicsforPartialDifferentialEquations173.
1ClassicationofLinearPartialDifferentialEquationsofKovalevskianType173.
2ClassicationofLinearPartialDifferentialEquationsofSecondOrder.
193.
3ClassicationofLinearSystemsofPartialDifferentialEquations213.
4ClassicationofDomainsandStatementofProblems.
263.
4.
1StationaryProcesses273.
4.
2NonstationaryProcesses.
283.
5ClassicationofSolutions.
324TheCauchy-KovalevskajaTheorem374.
1ClassicalVersion374.
2AbstractVersion40xixiiContents4.
3ConcludingRemarks.
434.
3.
1GeneralizationsoftheClassicalCauchy-KovalevskajaTheorem434.
3.
2GeneralizationsoftheAbstractCauchy-KovalevskajaTheorem444.
3.
3ApplicationsoftheAbstractCauchy-KovalevskajaTheorem455Holmgren'sUniquenessTheorem495.
1ClassicalVersion495.
2AbstractVersion525.
3ConcludingRemarks.
535.
3.
1ClassicalHolmgrenTheorem535.
3.
2AbstractHolmgrenTheorem546MethodofCharacteristics576.
1QuasilinearPartialDifferentialEquationsofFirstOrder576.
2TheNotionofCharacteristics:RelationtoSystemsofOrdinaryDifferentialEquations.
586.
3InuenceoftheInitialCondition.
596.
4ApplicationoftheInverseFunctionTheorem616.
5Summary646.
6Examples656.
6.
1ContinuityEquation656.
6.
2AnExampleofaCharacteristicCauchyProblem.
.
.
.
.
.
656.
7ConcludingRemarks.
667Burgers'Equation697.
1ClassicalBurgers'Equation697.
2OtherModelsRelatedtoBurgers'Equation.
737.
3ConcludingRemarks.
74PartII8LaplaceEquation—PropertiesofSolutions—StartingPointofEllipticTheory798.
1PoissonIntegralFormula798.
1.
1HowDoesPotentialTheoryComeintoPlay798.
1.
2Green'sFunctionandPoissonIntegralFormula.
.
.
.
.
.
.
828.
2PropertiesofHarmonicFunctions878.
2.
1MeanValueProperty878.
2.
2Maximum-MinimumPrinciple.
878.
2.
3RegularityofHarmonicFunctions888.
2.
4Weyl'sLemmaandInteriorRegularity898.
3OtherPropertiesofEllipticOperatorsorEllipticEquations.
.
.
.
.
.
918.
3.
1Hypoellipticity918.
3.
2LocalSolvability92Contentsxiii8.
4BoundaryValueProblemsofPotentialTheory.
938.
4.
1BasicBoundaryValueProblemsofPotentialTheory938.
4.
2HowtoUsePotentialsinRepresentationsofSolutions968.
4.
3IntegralEquationsofPotentialTheory999HeatEquation—PropertiesofSolutions—StartingPointofParabolicTheory1039.
1PotentialTheoryandRepresentationFormula1039.
2Maximum-MinimumPrinciple.
1059.
3QualitativePropertiesofSolutionsoftheCauchyProblemfortheHeatEquation1079.
3.
1Non-reversibilityinTime.
1089.
3.
2InniteSpeedofPropagation1089.
3.
3SmoothingEffect1099.
3.
4UniquenessofClassicalSolutionstotheCauchyProblem1109.
4MixedProblemsfortheHeatEquation1119.
4.
1BasicMixedProblems.
1119.
4.
2HowtoUseThermalPotentialsinRepresentationsofSolutions1139.
4.
3IntegralEquationsofMixedProblemsfortheHeatEquation11410WaveEquation—PropertiesofSolutions—StartingPointofHyperbolicTheory11910.
1d'Alembert'sRepresentationinR111910.
1.
1RegularityofSolutions12010.
1.
2FiniteSpeedofPropagationofPerturbations12110.
1.
3DomainofDependence.
12110.
1.
4Huygens'Principle12110.
2WaveModelswithSourcesorSinks12210.
3Kirchhoff'sRepresentationinR312210.
3.
1HowCantheReaderGuessKirchhoff'sFormula.
.
.
.
.
12310.
3.
2VericationofKirchhoff'sFormula12510.
4Kirchhoff'sRepresentationinR212710.
4.
1MethodofDescent.
12810.
5RepresentationFormulasinHigherDimensions12910.
5.
1OddSpaceDimension12910.
5.
2EvenSpaceDimension13010.
6PropagationofSingularities13110.
6.
1MoreAboutPropagationofSingularities.
13310.
7ConcludingRemarks.
13510.
7.
1DerivationofWaveLayerPotentials.
13610.
7.
2BasicMixedProblemsfortheWaveEquation138xivContents10.
7.
3HowtoUseWavePotentialsinRepresentationsofSolutions13910.
7.
4IntegralEquationfortheInteriorDirichletProblemfortheWaveEquation14010.
7.
5FinalCommentstoMixedProblems.
14111TheNotionofEnergyofSolutions:OneoftheMostImportantQuantities.
14711.
1EnergiesforSolutionstotheWaveEquation14711.
2ExamplesofEnergiesforOtherModels15111.
2.
1OneEnergyforSolutionstotheElasticWaveEquation15111.
2.
2EnergiesforSolutionstotheHeatEquation.
15211.
2.
3EnergiesforSolutionstotheSchrdingerEquation.
.
.
15211.
2.
4EnergiesforSolutionstothePlateEquation15311.
2.
5EnergiesforSolutionstoSpecialSemilinearWaveModels.
15311.
2.
6HowtoDeneEnergiesinGeneral15411.
3InuencesofLowerOrderTermstoQualitativePropertiesofSolutions15511.
3.
1WaveModelswithTermsofLowerOrder.
15511.
3.
2ClassicalDampedWaveModels15611.
3.
3WaveModelswithViscoelasticDamping15711.
3.
4Klein-GordonEquation.
15811.
3.
5PlateEquationswithLowerOrderTerms16011.
4BehaviorofLocalEnergies.
16011.
4.
1BehaviorofLocalEnergiesforSolutionstotheFreeWaveEquation.
16211.
4.
2BehaviorofLocalEnergiesforSolutionstotheElasticWaveEquation16311.
4.
3BehaviorofLocalEnergiesforSolutionstotheKlein-GordonEquation16411.
4.
4BehaviorofLocalEnergiesforSolutionstotheClassicalDampedWaveEquation16511.
4.
5BehaviorofLocalEnergiesforSolutionstotheViscoelasticDampedWaveEquation16611.
4.
6BehaviorofLocalEnergiesforSolutionstotheHeatEquation16711.
4.
7BehaviorofLocalEnergiesforSolutionstotheSchrdingerEquation169ContentsxvPartIII12PhaseSpaceAnalysisfortheHeatEquation17312.
1TheClassicalHeatEquation17312.
1.
1L2L2Estimates17412.
1.
2LpLqEstimatesontheConjugateLine.
17512.
1.
3LpLqEstimatesAwayoftheConjugateLine17512.
2TheClassicalHeatEquationwithMass17813PhaseSpaceAnalysisandSmoothingforSchrdingerEquations.
.
.
.
18113.
1LpLqEstimates18113.
1.
1TheClassicalSchrdingerEquation18113.
1.
2TheClassicalSchrdingerEquationwithMass18413.
2SmoothingEffectforSolutions18513.
2.
1LocalSmoothingPropertiesofSolutions.
18613.
2.
2GlobalSmoothingPropertiesofSolutions18614PhaseSpaceAnalysisforWaveModels19114.
1TheClassicalWaveModel19114.
2TheClassicalDampedWaveModel19614.
2.
1RepresentationofSolutionsbyUsingFourierMultipliers.
19614.
2.
2DecayBehaviorandDecayRateoftheWaveEnergy19814.
2.
3TheDiffusionPhenomenonforDampedWaveModels.
20614.
2.
4DecayBehaviorUnderAdditionalRegularityofData.
21014.
3ViscoelasticDampedWaveModel21114.
3.
1RepresentationofSolutionsbyUsingFourierMultipliers.
21214.
3.
2DecayBehaviorandDecayRateoftheWaveEnergy21414.
3.
3DecayBehaviorUnderAdditionalRegularityofData.
21514.
4Klein-GordonModel.
21714.
4.
1RepresentationofSolutionsbyUsingFourierMultipliers.
21714.
5Klein-GordonModelwithExternalDissipation.
21914.
6Klein-GordonModelwithViscoelasticDissipation.
22014.
7ConcludingRemarks.
22115PhaseSpaceAnalysisforPlateModels.
22715.
1TheClassicalPlateModel22715.
2TheClassicalDampedPlateModel.
22815.
2.
1RepresentationofSolutionsbyUsingFourierMultipliers.
228xviContents15.
2.
2DecayBehaviorandDecayRateofaSuitableEnergy23015.
2.
3EnergiesofHigherOrder.
23115.
3TheViscoelasticDampedPlateModel23215.
3.
1RepresentationofSolutionsbyUsingFourierMultipliers.
23315.
3.
2ConclusionsfromtheRepresentationFormulas.
23415.
4TheClassicalPlateModelwithMass.
23515.
5TheClassicalPlateModelwithMassandDissipation.
23615.
5.
1TheClassicalDampedPlateModelwithMass.
23615.
5.
2TheClassicalPlateModelwithMassandViscoelasticDissipation23716TheMethodofStationaryPhaseandApplications24116.
1L2L2Estimates24116.
2PhilosophyofOurApproachtoDeriveLpLqEstimatesontheConjugateLineforSolutionstotheWaveEquation.
.
.
.
.
.
.
24216.
3ALittmanTypeLemma24416.
4LpLqEstimatesforFourierMultiplierswithAmplitudesLocalizedinthePseudo-DifferentialZone24916.
5LpLqEstimatesontheConjugateLineforFourierMultiplierswithAmplitudesLocalizedintheHyperbolicZone25016.
6LpLqEstimatesontheConjugateLineforSolutionstotheWaveEquation25216.
7LpLqEstimatesAwayfromtheConjugateLine25716.
8LpLqEstimatesontheConjugateLineforSolutionstotheSchrdingerEquation25816.
8.
1PhilosophyofOurApproachtoDeriveLpLqEstimatesontheConjugateLineforSolutionstotheSchrdingerEquation25916.
8.
2ALittmanTypeLemma26016.
8.
3LpLqEstimatesforFourierMultiplierswithAmplitudesLocalizedinthePseudodifferentialZone26216.
8.
4LpLqEstimatesontheConjugateLineforFourierMultiplierswithAmplitudesLocalizedintheEvolutionZone26316.
8.
5LpLqEstimatesontheConjugateLineforSolutionstotheSchrdingerEquation.
26516.
9LpLqEstimatesontheConjugateLineforSolutionstothePlateEquation26616.
10ConcludingRemarks.
26816.
10.
1Littman'sLemma268ContentsxviiPartIV17SemilinearHeatModels.
27317.
1SemilinearHeatModelswithSourceNonlinearity27317.
1.
1FujitaDiscoveredtheCriticalExponent27417.
1.
2Self-SimilarSolutions27517.
1.
3AUsefulChangeofVariables.
27617.
1.
4BlowUpViaGlobalExistence.
27717.
2SemilinearHeatModelswithAbsorbingPowerNonlinearity.
.
.
.
28217.
2.
1Well-PosednessResultsfortheCauchyProblem.
.
.
.
.
.
28317.
2.
2InuenceoftheFujitaExponentontheProleofSolutions28518SemilinearClassicalDampedWaveModels29918.
1SemilinearClassicalDampedWaveModelswithSourceNonlinearity29918.
1.
1GlobalExistenceofSmallDataSolutions.
30018.
1.
2ApplicationoftheTestFunctionMethod.
30718.
2SemilinearClassicalDampedWaveModelswithAbsorbingNonlinearity.
31118.
2.
1GlobalExistenceofLargeDataSolutions.
31118.
2.
2LargeTimeAsymptotics31518.
3ConcludingRemarks.
31818.
3.
1SemilinearClassicalDampedWaveModelswithMassTerm31818.
3.
2SemilinearDampedWaveModelswithScale-InvariantDampingandMassTerm31919SemilinearWaveModelswithaSpecialStructuralDissipation.
.
.
.
.
.
.
32519.
1SemilinearWaveModelswithaSpecialStructuralDampingTerm32519.
2LpLqEstimatesNotNecessarilyontheConjugateLine.
.
.
.
.
.
.
32619.
3StructurallyDampedWaveModelswithNonlinearityjjDjaujp33019.
3.
1MainResult33019.
3.
2Proof.
33119.
3.
3Optimality33419.
4StructurallyDampedWaveModelswithNonlinearityjutjp.
.
.
.
.
.
33619.
4.
1MainResult33619.
4.
2Proof.
33719.
5ConcludingRemarks.
34319.
5.
1SemilinearViscoelasticDampedWaveModels34319.
5.
2SemilinearStructurallyDamped-EvolutionModels.
345xviiiContents20SemilinearClassicalWaveModels.
35120.
1SemilinearClassicalWaveModelswithSourceNonlinearity.
.
.
.
35120.
1.
1LocalExistence(inTime)ofSobolevSolutions.
.
.
.
.
.
.
35220.
1.
2NonexistenceofGlobal(inTime)ClassicalSolutions35520.
1.
3SomeRemarks:LifeSpanEstimates35720.
2SemilinearClassicalWaveModelswithAbsorbingNonlinearity35820.
3ConcludingRemarks.
36220.
3.
1StraussExponentVersusFujitaExponent36220.
3.
2ASpecialClassofQuasilinearWaveEquationswithTime-DependentSpeedofPropagation36321SemilinearSchrdingerModels.
36721.
1ExamplesofSemilinearSchrdingerModels36721.
2HowDoWeArriveataCriticalExponent36821.
3SemilinearModelswithPowerNonlinearityintheSubcriticalCasewithL2Data36921.
4SemilinearModelswithPowerNonlinearityintheSubcriticalCasewithH1Data37521.
5ConcludingRemarks.
38021.
5.
1SomeRemarkstoCriticalandSupercriticalCases.
.
.
.
.
38021.
5.
2SomeRemarkstoCriticalCases38121.
5.
3SomeRemarkstotheAsymptoticalProle38122LinearHyperbolicSystems38322.
1PlaneWaveSolutions38322.
2SymmetricSystemswithConstantCoefcients.
38422.
3HyperbolicSystemswithConstantCoefcients38622.
4LinearStrictlyHyperbolicSystemsin1d:MethodofCharacteristics.
38922.
5EnergyInequalitiesforLinearSymmetricHyperbolicSystems.
39622.
6ConcludingRemarks.
39822.
6.
1Well-PosednessforLinearSymmetricHyperbolicSystems.
39822.
6.
2Well-PosednessforLinearStrictlyHyperbolicSystems.
399PartV23ResearchProjectsforBeginners40523.
1ApplicationsoftheAbstractCauchy-KovalevskajaandHolmgrenTheorems40523.
2TheRobinProblemfortheHeatEquationinanInteriorDomain407Contentsxix23.
3LpLqDecayEstimatesforSolutionstotheHeatEquationwithMass40823.
4TheCauchyProblemfortheFreeWaveEquationinModulationSpaces40823.
5TheDiffusionPhenomenonforClassicalDampedKlein-GordonModels40923.
6TheDiffusionPhenomenonforClassicalDampedPlateModels.
41023.
7TheDiffusionPhenomenonforDampedWaveModelswithSource.
41123.
8ProleofSolutionstoClassicalDampedWaveswithSource.
.
.
.
41323.
9LpLqEstimatesforSolutionstoStructurallyDamped-EvolutionModels41523.
10SemilinearHeatModelswithSourcePowerNonlinearities.
.
.
.
.
.
41623.
11SemilinearStructurallyDamped-EvolutionEquations41823.
12SemilinearStructurallyDampedWaveEquations.
41823.
13Scale-Invariant-EvolutionModelswithMass,DissipationandaPowerNonlinearity41924BackgroundMaterial42324.
1BasicsofFourierTransformation42324.
1.
1ApplicationtoSpacesofInnitelyDifferentiableFunctions42424.
1.
2ApplicationtoLpSpaces42724.
1.
3ApplicationtoTemperedDistributions43124.
1.
4ApplicationtoHsSpaces43224.
2TheoryofFourierMultipliers43424.
2.
1ModiedBesselFunctions43424.
2.
2LpEstimatesforModelOscillatingIntegrals.
43524.
3FunctionSpaces.
44524.
4SomeToolsfromDistributionTheory45124.
5UsefulInequalities455References.
465Notations475Index477
EbertMichaelReissigMethodsforPartialDifferentialEquationsQualitativePropertiesofSolutions,PhaseSpaceAnalysis,SemilinearModelsMarceloR.
EbertUniversityofSQaoPauloDepartmentofComputingandMathematicsRibeiroPreto,SoPaulo,BrazilMichaelReissigTUBergakademieFreibergInstituteofAppliedAnalysisFreiberg,GermanyISBN978-3-319-66455-2ISBN978-3-319-66456-9(eBook)https://doi.
org/10.
1007/978-3-319-66456-9LibraryofCongressControlNumber:2017963017MathematicsSubjectClassication(2010):35-01,35-02,35A01,35A02,35A10,35B30,35B33,35B40,35B44,35E20,35F20,35F35,35J05,35J10,35J99,35K05,35K99,35L05,35L45,35L71,35L99SpringerInternationalPublishingAG2018Thisworkissubjecttocopyright.
AllrightsarereservedbythePublisher,whetherthewholeorpartofthematerialisconcerned,specicallytherightsoftranslation,reprinting,reuseofillustrations,recitation,broadcasting,reproductiononmicrolmsorinanyotherphysicalway,andtransmissionorinformationstorageandretrieval,electronicadaptation,computersoftware,orbysimilarordissimilarmethodologynowknownorhereafterdeveloped.
Theuseofgeneraldescriptivenames,registerednames,trademarks,servicemarks,etc.
inthispublicationdoesnotimply,evenintheabsenceofaspecicstatement,thatsuchnamesareexemptfromtherelevantprotectivelawsandregulationsandthereforefreeforgeneraluse.
Thepublisher,theauthorsandtheeditorsaresafetoassumethattheadviceandinformationinthisbookarebelievedtobetrueandaccurateatthedateofpublication.
Neitherthepublishernortheauthorsortheeditorsgiveawarranty,expressorimplied,withrespecttothematerialcontainedhereinorforanyerrorsoromissionsthatmayhavebeenmade.
Thepublisherremainsneutralwithregardtojurisdictionalclaimsinpublishedmapsandinstitutionalafliations.
Printedonacid-freepaperThisbookispublishedunderthetradenameBirkhuser,www.
birkhauser-science.
comTheregisteredcompanyisSpringerInternationalPublishingAGTheregisteredcompanyaddressis:Gewerbestrasse11,6330Cham,SwitzerlandDedicatedtoourwivesHelenaandStefPrefaceItistheaimofthisbooktomotivateyoungmathematiciansatthepostgraduateleveltostartstudyingdifferenttopicsofthetheoryofpartialdifferentialequations.
ThebookisaddressedtoMasterandPhDstudentswithinterestinthistheory.
AfterattendingintroductorycoursesonPDE's,usuallyattheendofundergraduatestudies,thebackgroundsofthosestudentsmayvarywidely.
SometimesthetheoryonPDE'sisreducedtoFourier'smethodandintegraltransformationsonly.
ThemainpurposeofthisbookistoamplifyanadvancedcourseonPDE'sduringgraduatestudies.
Thebookprovidesanoverviewondifferenttopicsofthetheoryofpartialdifferentialequations.
Asitisannouncedinthetitle,theexplanationofqualitativepropertiesofsolutionsoflinearmodels,theintroductiontophasespaceanalysisontheonehandandmodernmethodshowtotreatsemilinearmodelsontheotherhand,formthecoreofthebook.
TheauthorshavechosenthesesubtitlesbecauseadeeperknowledgeofthesetopicsisanimportantbasefromwhichtoapplyordevelopthetheoryofPDE's.
Usually,introductorycoursesonPDE'scontainonlyveryfewpropertiesofsolutionstobasicPDE's.
WewillillustratequalitativepropertiesofsolutionsofmodelequationsshowingfundamentaldifferencesbetweenpropertiesofsolutionstoLaplace,heat,waveorSchrdingerequations.
Adeepknowledgeofsuchprop-ertieshelpsinunderstandingtheapplicabilityofdifferentmethodsortechniquestotreatmorecomplexmodels.
PhasespaceanalysisiswidelyappliedinalotofbranchesofthetheoryofPDE's.
OnlyaverycarefuldescriptionofFouriertransformoffunctionsorevendistributionstogetherwithdecompositiontechniquesofthephasespaceallowsforattackingalotofproblemsfromthetheoryofpartialdifferentialequations.
WithouthavingtoolsfromWKBanalysis,thetheoryofpseudo-differentialorpara-differentialoperators,alotofmodelscannotbetreatedinanoptimalway.
Forthisreasontheauthorsincludedchaptersonbasicsofphasespaceanalysis.
Themovefromlinearmodelstononlinearonesisabigchallenge.
Evenifoneaddsthemostsimplenonlinearitiesjujpor˙jujp1uasanonlinearright-handsideinalinearmodelitcausesalotofnewdifculties.
Sometimessuchatermdeterminesnewtrendsinthetheory.
Theauthorsshowbysemilinearheat,waveorSchrdingerviiviiiPrefacemodelsthebiginuenceofthesenonlinearitiesonmethods,trendsandexpectedresults.
Adeepknowledgeofhowtotreatsemilinearmodelssimpliesthemovetounderstandquasi-ornonlinearmodelsaswell.
TheauthorshaveyearsofexperiencegivingcoursesonPDE'satundergraduateandgraduatelevelandsupervisingPhDstudents.
Thebookcontainstheircombinedteachingandsupervisingexpertise.
Thecourseswereheldatvariousuniversitiesthroughouttheworld.
In2009,therstauthorgaveacourseabouttheCauchyproblemforpartialdifferentialoperatorswithinthe27thBrazilianMathematicsColloquiumatInstitutoNacionaldeMatemáticaPuraeAplicada(IMPA)inRiodeJaneiro.
UpontheinvitationofProf.
SandraLucente,thesecondauthorstayedattheUniversityofBariinItalyduringNovember2013,andgaveaseriesoflecturesonpartialdifferentialequationswithinthe"ProjectMessaggeridellaConoscenza2012,ID424",supportedbythegovernmentofItaly.
TheaudiencewascomposedofMasterandPhDstudentsnotonlyfromUniversityofBari.
Thiscomprehensivecoursewasonlyoneofaseriesofninecourseson"BasicsofPartialDifferentialEquations"thesecondauthorgaveduringtheperiod2007–2016attheShanghaiJiao-TongUniversity,KazakhNationalUniversityAlFarabyAlma-AtyinKaza-khstan,theEurasianNationalUniversityL.
N.
GumilevaAstanainKazakhstan,theHanoiNationalUniversityofEducationandtheHanoiUniversityofScienceandTechnologyinVietnam.
Thesecondauthorsince2002givesthecourse"PartialDifferentialEquations1/2"attheFacultyforMathematicsandComputerScienceofTechnicalUniversityBergakademieFreiberg,andherehesupervised15PhDstudents,severalofthemfromabroad.
TherstauthorspenttheperiodJuly2014–July2015,hissabbaticalyear,inFreiberg.
Duringthistimehegaveadvancedseminarson"PartialDifferentialEquations"forMasterstudents.
Fromallactivitiesarosethejointideatowritethisbook.
Itwillbeourgreatpleasureshouldthisbookstimulateyoungmathematicianstobecomefamiliarwiththebeautifultheoryofpartialdifferentialequations.
RibeiroPreto,SoPaulo,BrazilMarceloR.
EbertFreiberg,GermanyMichaelReissigJune2017AcknowledgementsTheideatowritethisbookaroseduringthestayoftherstauthor(July2014–July2015)attheInstituteofAppliedAnalysisatTUBergakademieFreiberg.
ThestayoftherstauthorwassupportedbyFundaodeAmparoàPesquisadoEstadodeSoPaulo(FAPESP),grant2013/20297-8.
ThebookwascompletedwithintheDFGprojectRE961/21-1andFAPESPGrant2015/16038-2.
TheauthorsthankVladimirGeorgiev,SandraLucente,WinfriedSickel,MitsuruSugimoto,HiroyukiTakamuraandKarenYagdjianforfruitfuldiscussionsonthecontentofsomepartsofthisbook.
Moreover,theauthorsthankformerPhDstudentsAbdelhamidMohammedDjaouti,ChristianJh,WanderleyNunesdoNascimento,AlessandroPalmieriandMaximilianReichforreadingsomeofthechapters.
Finally,wethankthestafffromBirkhuserpublishinghouse,inparticular,SarahGoobandDr.
ThomasHemping,forthefruitfulco-operationinpreparingthenalversionofthisbook.
ixContentsPartI1Introduction32PartialDifferentialEquationsinModels72.
1AGeneralConservationLaw.
72.
2TransportorConvection82.
3Diffusion92.
4StationaryModels.
102.
5WavesinAcoustics112.
6QuantumMechanics132.
7Gas-andHydrodynamics.
142.
8ConcludingRemarks.
143BasicsforPartialDifferentialEquations173.
1ClassicationofLinearPartialDifferentialEquationsofKovalevskianType173.
2ClassicationofLinearPartialDifferentialEquationsofSecondOrder.
193.
3ClassicationofLinearSystemsofPartialDifferentialEquations213.
4ClassicationofDomainsandStatementofProblems.
263.
4.
1StationaryProcesses273.
4.
2NonstationaryProcesses.
283.
5ClassicationofSolutions.
324TheCauchy-KovalevskajaTheorem374.
1ClassicalVersion374.
2AbstractVersion40xixiiContents4.
3ConcludingRemarks.
434.
3.
1GeneralizationsoftheClassicalCauchy-KovalevskajaTheorem434.
3.
2GeneralizationsoftheAbstractCauchy-KovalevskajaTheorem444.
3.
3ApplicationsoftheAbstractCauchy-KovalevskajaTheorem455Holmgren'sUniquenessTheorem495.
1ClassicalVersion495.
2AbstractVersion525.
3ConcludingRemarks.
535.
3.
1ClassicalHolmgrenTheorem535.
3.
2AbstractHolmgrenTheorem546MethodofCharacteristics576.
1QuasilinearPartialDifferentialEquationsofFirstOrder576.
2TheNotionofCharacteristics:RelationtoSystemsofOrdinaryDifferentialEquations.
586.
3InuenceoftheInitialCondition.
596.
4ApplicationoftheInverseFunctionTheorem616.
5Summary646.
6Examples656.
6.
1ContinuityEquation656.
6.
2AnExampleofaCharacteristicCauchyProblem.
.
.
.
.
.
656.
7ConcludingRemarks.
667Burgers'Equation697.
1ClassicalBurgers'Equation697.
2OtherModelsRelatedtoBurgers'Equation.
737.
3ConcludingRemarks.
74PartII8LaplaceEquation—PropertiesofSolutions—StartingPointofEllipticTheory798.
1PoissonIntegralFormula798.
1.
1HowDoesPotentialTheoryComeintoPlay798.
1.
2Green'sFunctionandPoissonIntegralFormula.
.
.
.
.
.
.
828.
2PropertiesofHarmonicFunctions878.
2.
1MeanValueProperty878.
2.
2Maximum-MinimumPrinciple.
878.
2.
3RegularityofHarmonicFunctions888.
2.
4Weyl'sLemmaandInteriorRegularity898.
3OtherPropertiesofEllipticOperatorsorEllipticEquations.
.
.
.
.
.
918.
3.
1Hypoellipticity918.
3.
2LocalSolvability92Contentsxiii8.
4BoundaryValueProblemsofPotentialTheory.
938.
4.
1BasicBoundaryValueProblemsofPotentialTheory938.
4.
2HowtoUsePotentialsinRepresentationsofSolutions968.
4.
3IntegralEquationsofPotentialTheory999HeatEquation—PropertiesofSolutions—StartingPointofParabolicTheory1039.
1PotentialTheoryandRepresentationFormula1039.
2Maximum-MinimumPrinciple.
1059.
3QualitativePropertiesofSolutionsoftheCauchyProblemfortheHeatEquation1079.
3.
1Non-reversibilityinTime.
1089.
3.
2InniteSpeedofPropagation1089.
3.
3SmoothingEffect1099.
3.
4UniquenessofClassicalSolutionstotheCauchyProblem1109.
4MixedProblemsfortheHeatEquation1119.
4.
1BasicMixedProblems.
1119.
4.
2HowtoUseThermalPotentialsinRepresentationsofSolutions1139.
4.
3IntegralEquationsofMixedProblemsfortheHeatEquation11410WaveEquation—PropertiesofSolutions—StartingPointofHyperbolicTheory11910.
1d'Alembert'sRepresentationinR111910.
1.
1RegularityofSolutions12010.
1.
2FiniteSpeedofPropagationofPerturbations12110.
1.
3DomainofDependence.
12110.
1.
4Huygens'Principle12110.
2WaveModelswithSourcesorSinks12210.
3Kirchhoff'sRepresentationinR312210.
3.
1HowCantheReaderGuessKirchhoff'sFormula.
.
.
.
.
12310.
3.
2VericationofKirchhoff'sFormula12510.
4Kirchhoff'sRepresentationinR212710.
4.
1MethodofDescent.
12810.
5RepresentationFormulasinHigherDimensions12910.
5.
1OddSpaceDimension12910.
5.
2EvenSpaceDimension13010.
6PropagationofSingularities13110.
6.
1MoreAboutPropagationofSingularities.
13310.
7ConcludingRemarks.
13510.
7.
1DerivationofWaveLayerPotentials.
13610.
7.
2BasicMixedProblemsfortheWaveEquation138xivContents10.
7.
3HowtoUseWavePotentialsinRepresentationsofSolutions13910.
7.
4IntegralEquationfortheInteriorDirichletProblemfortheWaveEquation14010.
7.
5FinalCommentstoMixedProblems.
14111TheNotionofEnergyofSolutions:OneoftheMostImportantQuantities.
14711.
1EnergiesforSolutionstotheWaveEquation14711.
2ExamplesofEnergiesforOtherModels15111.
2.
1OneEnergyforSolutionstotheElasticWaveEquation15111.
2.
2EnergiesforSolutionstotheHeatEquation.
15211.
2.
3EnergiesforSolutionstotheSchrdingerEquation.
.
.
15211.
2.
4EnergiesforSolutionstothePlateEquation15311.
2.
5EnergiesforSolutionstoSpecialSemilinearWaveModels.
15311.
2.
6HowtoDeneEnergiesinGeneral15411.
3InuencesofLowerOrderTermstoQualitativePropertiesofSolutions15511.
3.
1WaveModelswithTermsofLowerOrder.
15511.
3.
2ClassicalDampedWaveModels15611.
3.
3WaveModelswithViscoelasticDamping15711.
3.
4Klein-GordonEquation.
15811.
3.
5PlateEquationswithLowerOrderTerms16011.
4BehaviorofLocalEnergies.
16011.
4.
1BehaviorofLocalEnergiesforSolutionstotheFreeWaveEquation.
16211.
4.
2BehaviorofLocalEnergiesforSolutionstotheElasticWaveEquation16311.
4.
3BehaviorofLocalEnergiesforSolutionstotheKlein-GordonEquation16411.
4.
4BehaviorofLocalEnergiesforSolutionstotheClassicalDampedWaveEquation16511.
4.
5BehaviorofLocalEnergiesforSolutionstotheViscoelasticDampedWaveEquation16611.
4.
6BehaviorofLocalEnergiesforSolutionstotheHeatEquation16711.
4.
7BehaviorofLocalEnergiesforSolutionstotheSchrdingerEquation169ContentsxvPartIII12PhaseSpaceAnalysisfortheHeatEquation17312.
1TheClassicalHeatEquation17312.
1.
1L2L2Estimates17412.
1.
2LpLqEstimatesontheConjugateLine.
17512.
1.
3LpLqEstimatesAwayoftheConjugateLine17512.
2TheClassicalHeatEquationwithMass17813PhaseSpaceAnalysisandSmoothingforSchrdingerEquations.
.
.
.
18113.
1LpLqEstimates18113.
1.
1TheClassicalSchrdingerEquation18113.
1.
2TheClassicalSchrdingerEquationwithMass18413.
2SmoothingEffectforSolutions18513.
2.
1LocalSmoothingPropertiesofSolutions.
18613.
2.
2GlobalSmoothingPropertiesofSolutions18614PhaseSpaceAnalysisforWaveModels19114.
1TheClassicalWaveModel19114.
2TheClassicalDampedWaveModel19614.
2.
1RepresentationofSolutionsbyUsingFourierMultipliers.
19614.
2.
2DecayBehaviorandDecayRateoftheWaveEnergy19814.
2.
3TheDiffusionPhenomenonforDampedWaveModels.
20614.
2.
4DecayBehaviorUnderAdditionalRegularityofData.
21014.
3ViscoelasticDampedWaveModel21114.
3.
1RepresentationofSolutionsbyUsingFourierMultipliers.
21214.
3.
2DecayBehaviorandDecayRateoftheWaveEnergy21414.
3.
3DecayBehaviorUnderAdditionalRegularityofData.
21514.
4Klein-GordonModel.
21714.
4.
1RepresentationofSolutionsbyUsingFourierMultipliers.
21714.
5Klein-GordonModelwithExternalDissipation.
21914.
6Klein-GordonModelwithViscoelasticDissipation.
22014.
7ConcludingRemarks.
22115PhaseSpaceAnalysisforPlateModels.
22715.
1TheClassicalPlateModel22715.
2TheClassicalDampedPlateModel.
22815.
2.
1RepresentationofSolutionsbyUsingFourierMultipliers.
228xviContents15.
2.
2DecayBehaviorandDecayRateofaSuitableEnergy23015.
2.
3EnergiesofHigherOrder.
23115.
3TheViscoelasticDampedPlateModel23215.
3.
1RepresentationofSolutionsbyUsingFourierMultipliers.
23315.
3.
2ConclusionsfromtheRepresentationFormulas.
23415.
4TheClassicalPlateModelwithMass.
23515.
5TheClassicalPlateModelwithMassandDissipation.
23615.
5.
1TheClassicalDampedPlateModelwithMass.
23615.
5.
2TheClassicalPlateModelwithMassandViscoelasticDissipation23716TheMethodofStationaryPhaseandApplications24116.
1L2L2Estimates24116.
2PhilosophyofOurApproachtoDeriveLpLqEstimatesontheConjugateLineforSolutionstotheWaveEquation.
.
.
.
.
.
.
24216.
3ALittmanTypeLemma24416.
4LpLqEstimatesforFourierMultiplierswithAmplitudesLocalizedinthePseudo-DifferentialZone24916.
5LpLqEstimatesontheConjugateLineforFourierMultiplierswithAmplitudesLocalizedintheHyperbolicZone25016.
6LpLqEstimatesontheConjugateLineforSolutionstotheWaveEquation25216.
7LpLqEstimatesAwayfromtheConjugateLine25716.
8LpLqEstimatesontheConjugateLineforSolutionstotheSchrdingerEquation25816.
8.
1PhilosophyofOurApproachtoDeriveLpLqEstimatesontheConjugateLineforSolutionstotheSchrdingerEquation25916.
8.
2ALittmanTypeLemma26016.
8.
3LpLqEstimatesforFourierMultiplierswithAmplitudesLocalizedinthePseudodifferentialZone26216.
8.
4LpLqEstimatesontheConjugateLineforFourierMultiplierswithAmplitudesLocalizedintheEvolutionZone26316.
8.
5LpLqEstimatesontheConjugateLineforSolutionstotheSchrdingerEquation.
26516.
9LpLqEstimatesontheConjugateLineforSolutionstothePlateEquation26616.
10ConcludingRemarks.
26816.
10.
1Littman'sLemma268ContentsxviiPartIV17SemilinearHeatModels.
27317.
1SemilinearHeatModelswithSourceNonlinearity27317.
1.
1FujitaDiscoveredtheCriticalExponent27417.
1.
2Self-SimilarSolutions27517.
1.
3AUsefulChangeofVariables.
27617.
1.
4BlowUpViaGlobalExistence.
27717.
2SemilinearHeatModelswithAbsorbingPowerNonlinearity.
.
.
.
28217.
2.
1Well-PosednessResultsfortheCauchyProblem.
.
.
.
.
.
28317.
2.
2InuenceoftheFujitaExponentontheProleofSolutions28518SemilinearClassicalDampedWaveModels29918.
1SemilinearClassicalDampedWaveModelswithSourceNonlinearity29918.
1.
1GlobalExistenceofSmallDataSolutions.
30018.
1.
2ApplicationoftheTestFunctionMethod.
30718.
2SemilinearClassicalDampedWaveModelswithAbsorbingNonlinearity.
31118.
2.
1GlobalExistenceofLargeDataSolutions.
31118.
2.
2LargeTimeAsymptotics31518.
3ConcludingRemarks.
31818.
3.
1SemilinearClassicalDampedWaveModelswithMassTerm31818.
3.
2SemilinearDampedWaveModelswithScale-InvariantDampingandMassTerm31919SemilinearWaveModelswithaSpecialStructuralDissipation.
.
.
.
.
.
.
32519.
1SemilinearWaveModelswithaSpecialStructuralDampingTerm32519.
2LpLqEstimatesNotNecessarilyontheConjugateLine.
.
.
.
.
.
.
32619.
3StructurallyDampedWaveModelswithNonlinearityjjDjaujp33019.
3.
1MainResult33019.
3.
2Proof.
33119.
3.
3Optimality33419.
4StructurallyDampedWaveModelswithNonlinearityjutjp.
.
.
.
.
.
33619.
4.
1MainResult33619.
4.
2Proof.
33719.
5ConcludingRemarks.
34319.
5.
1SemilinearViscoelasticDampedWaveModels34319.
5.
2SemilinearStructurallyDamped-EvolutionModels.
345xviiiContents20SemilinearClassicalWaveModels.
35120.
1SemilinearClassicalWaveModelswithSourceNonlinearity.
.
.
.
35120.
1.
1LocalExistence(inTime)ofSobolevSolutions.
.
.
.
.
.
.
35220.
1.
2NonexistenceofGlobal(inTime)ClassicalSolutions35520.
1.
3SomeRemarks:LifeSpanEstimates35720.
2SemilinearClassicalWaveModelswithAbsorbingNonlinearity35820.
3ConcludingRemarks.
36220.
3.
1StraussExponentVersusFujitaExponent36220.
3.
2ASpecialClassofQuasilinearWaveEquationswithTime-DependentSpeedofPropagation36321SemilinearSchrdingerModels.
36721.
1ExamplesofSemilinearSchrdingerModels36721.
2HowDoWeArriveataCriticalExponent36821.
3SemilinearModelswithPowerNonlinearityintheSubcriticalCasewithL2Data36921.
4SemilinearModelswithPowerNonlinearityintheSubcriticalCasewithH1Data37521.
5ConcludingRemarks.
38021.
5.
1SomeRemarkstoCriticalandSupercriticalCases.
.
.
.
.
38021.
5.
2SomeRemarkstoCriticalCases38121.
5.
3SomeRemarkstotheAsymptoticalProle38122LinearHyperbolicSystems38322.
1PlaneWaveSolutions38322.
2SymmetricSystemswithConstantCoefcients.
38422.
3HyperbolicSystemswithConstantCoefcients38622.
4LinearStrictlyHyperbolicSystemsin1d:MethodofCharacteristics.
38922.
5EnergyInequalitiesforLinearSymmetricHyperbolicSystems.
39622.
6ConcludingRemarks.
39822.
6.
1Well-PosednessforLinearSymmetricHyperbolicSystems.
39822.
6.
2Well-PosednessforLinearStrictlyHyperbolicSystems.
399PartV23ResearchProjectsforBeginners40523.
1ApplicationsoftheAbstractCauchy-KovalevskajaandHolmgrenTheorems40523.
2TheRobinProblemfortheHeatEquationinanInteriorDomain407Contentsxix23.
3LpLqDecayEstimatesforSolutionstotheHeatEquationwithMass40823.
4TheCauchyProblemfortheFreeWaveEquationinModulationSpaces40823.
5TheDiffusionPhenomenonforClassicalDampedKlein-GordonModels40923.
6TheDiffusionPhenomenonforClassicalDampedPlateModels.
41023.
7TheDiffusionPhenomenonforDampedWaveModelswithSource.
41123.
8ProleofSolutionstoClassicalDampedWaveswithSource.
.
.
.
41323.
9LpLqEstimatesforSolutionstoStructurallyDamped-EvolutionModels41523.
10SemilinearHeatModelswithSourcePowerNonlinearities.
.
.
.
.
.
41623.
11SemilinearStructurallyDamped-EvolutionEquations41823.
12SemilinearStructurallyDampedWaveEquations.
41823.
13Scale-Invariant-EvolutionModelswithMass,DissipationandaPowerNonlinearity41924BackgroundMaterial42324.
1BasicsofFourierTransformation42324.
1.
1ApplicationtoSpacesofInnitelyDifferentiableFunctions42424.
1.
2ApplicationtoLpSpaces42724.
1.
3ApplicationtoTemperedDistributions43124.
1.
4ApplicationtoHsSpaces43224.
2TheoryofFourierMultipliers43424.
2.
1ModiedBesselFunctions43424.
2.
2LpEstimatesforModelOscillatingIntegrals.
43524.
3FunctionSpaces.
44524.
4SomeToolsfromDistributionTheory45124.
5UsefulInequalities455References.
465Notations475Index477
- adds66456.com相关文档
- farmers66456.com
- Chr966456.com
- tus66456.com
- 黑鱼66456.com
- Monographs66456.com
- 核电66456.com
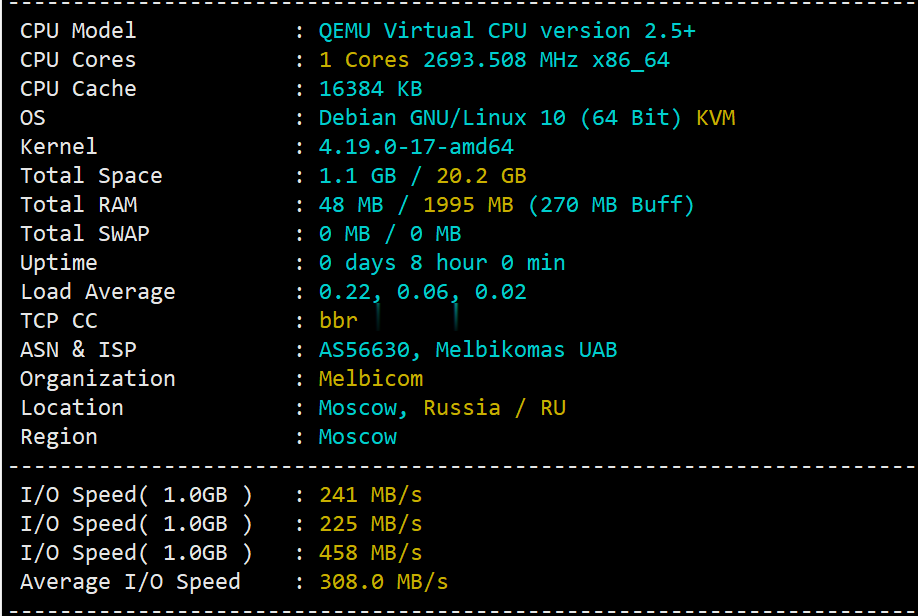
简单测评melbicom俄罗斯莫斯科数据中心的VPS,三网CN2回国,电信双程cn2
melbicom从2015年就开始运作了,在国内也是有一定的粉丝群,站长最早是从2017年开始介绍melbicom。上一次测评melbicom是在2018年,由于期间有不少人持续关注这个品牌,而且站长貌似也听说过路由什么的有变动的迹象。为此,今天重新对莫斯科数据中心的VPS进行一次简单测评,数据仅供参考。官方网站: https://melbicom.net比特币、信用卡、PayPal、支付宝、银联...
UCloud云服务器香港临时补货,(Intel)CN2 GIA优化线路,上车绝佳时机
至今为止介绍了很多UCLOUD云服务器的促销活动,UCLOUD业者以前看不到我们的个人用户,即使有促销活动,续费也很少。现在新用户的折扣力很大,包括旧用户在内也有一部分折扣。结果,我们的用户是他们的生存动力。没有共享他们的信息的理由是比较受欢迎的香港云服务器CN2GIA线路产品缺货。这不是刚才看到邮件注意和刘先生的通知,而是补充UCLOUD香港云服务器、INTELCPU配置的服务器。如果我们需要他...

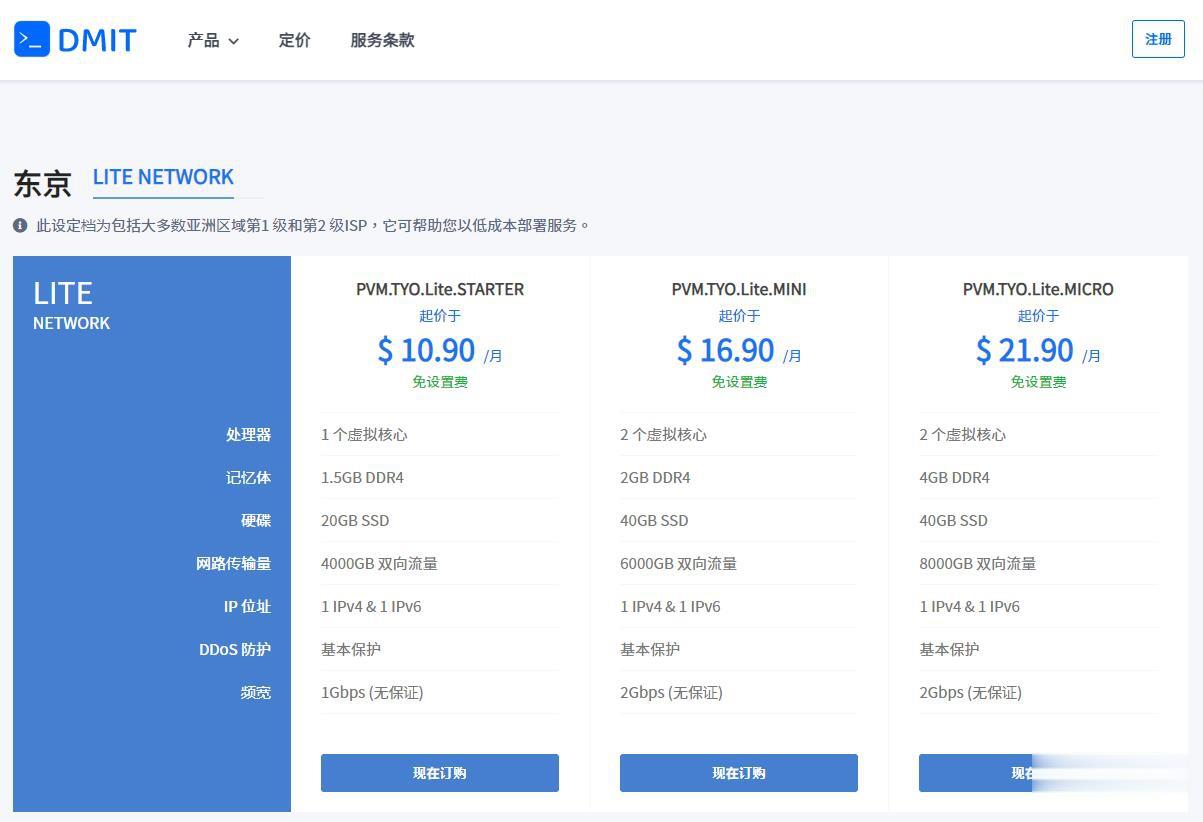
DMIT$10.9/月,日本VPS/三网直连/1核1.5G内存/20GB存储/1Gbps端口
优惠码年付一次性5折优惠码:TYO-Lite-Open-Beta-1y-50OFF永久8折优惠码:TYO-Lite-Open-Beta-Recur-20OFF日本vpsCPU内存SSD流量带宽价格购买1核1.5G20 GB4 TB1Gbps$10.9/月购买2核2 G40 GB6 TB1Gbps$16.9/月购买2核4 G60 GB8 TB1Gbps$21.9/月购买4核4 G80 GB12 TB...
66456.com为你推荐
-
摩拜超15分钟加钱摩拜单车免费卡和5元90天能叠加吗敬汉卿姓名被抢注身份证信息被抢注12306账号怎么办怎么查询商标想要知道一个商标是否被注册,在哪里查到的比较权威?今日油条联通大王卡看今日头条免流量吗?曹谷兰曹谷兰事件 有吧友知道吗长尾关键词挖掘工具大家是怎么挖掘长尾关键词的?103838.com39052.com这电影网支持网页观看吗?yinrentangzimotang氨基酸洗发水的功效咋样?www4399com4399小游戏 请记住本站网站 4399.urlwww.diediao.com谁知道台湾的拼音怎么拼啊?有具体的对照表最好!