transfowww.hhh258
www.hhh258 时间:2021-03-22 阅读:()
TheMulti-Scale3D-1DCompatibilityScoringforInverseProteinFoldingProblemKentaroOnizuka~,MasayukiAkahoshi,MasatoIshikawaInstituteforNewGenerationComputerTechnology(ICOT)1-4-28,Mita,Minat.
o-ku,Tokyo,108Japanonizuka@icot.
or.
jpPhone:-t-81-3-3456-3192,Fax:+81-3-3456-1618KiyoshiAsaiElectrotechnicalLaboratory(ETL)1-1-4,Umezono,Tsukuba,Ibaraki,305Japan~ai@etl.
go.
jpFax:+81-298-585939AbstractTimapplicttbilityoftheM'ulti-Sc,lcStr.
uctuveDc-.
~criptiou(MSSD)schcm.
ctoth.
ci,.
ecvsc@ddingpcobl,m.
~wasinvcstiyatcd.
A,.
MSSDvcprcsc.
lt.
t.
~ct.
/Dproteinstvm'tu'rcwithmultipb:symbolicse-qlte:/t('c.
%II,/le:7"ctin("setact.
arcsm'~:rcprcsc.
n.
tcdwithth.
c.
~cqtu:ncce,tlowlevels,tlu.
m.
iddlcscalestruc-tm'n.
lm.
otif.
~a.
tm.
'iddb:Iwvcls.
a,d91obaltopologyathigh.
lc'pels.
Each.
symbolintit.
(:symboh:csc-qucuccdenotesatypeoflocalstructureofthelevelscah~.
ThestructurefragmcTtts,.
.
recl,.
ssificdatc,ch.
re:alelevelVeSl.
,ccth,elyacco'rdi~tfltoth.
cshapea~utthectt.
Trivonmcntarouttdthe:fragments:h.
o'tvth.
c.
struct'utvise:tTJoscdtotimsolre:heorb'uricdi,.
th.
r:mole.
cult.
Imodeledth.
c.
pvopc.
,.
sityofwn~rm.
iTto-acidscq'tzt:Tu'ctoth.
cxl.
r.
uctavcfcayTncttttype(i.
c.
.
pvimo.
ryconstraint)~tteachs,hh"m'l.
Th.
elocalpvopc.
n.
sityis.
therefore,m.
odclcdatsm,llscale(low)b"vcl.
~.
.
u.
,hilcth.
c.
qlob,.
lpr(qm,.
sity7nodelcdl,.
7~1cm',.
lc(high.
)levels.
Th.
us.
mqmtTmsi,9alltheprim.
a.
ryconstvai.
n.
ts.
,.
']DpvotciTt.
strm't,.
rc.
yiddsmtamino-acid.
sequence.
profile.
Ee',luatiTt9thefitofvna'mDtoacidscqm,.
cctotimprofih'dcri'm:dfrom.
theknown31)protci',,st.
r,.
ctuw'.
.
,u'canidcn-tz~f!
lmh.
ich3Dstr.
m'rm',theflivcttam.
ino-acidsc-quc.
'n.
ccwo.
,.
hlflddi,to,lch.
ccl,:('dwluth~ram.
'-1Currently~tMatsushitaResearchInstituteTokyo,Inc.
3-ll)-1tlig~himita.
Tama-ku.
Kaw~us~ki21.
t.
,btl)~UlE-Mail:.
uizuka:~,~mrit.
mci.
('o.
jl)hon(,:+81-.
1.
1-911-635I.
l";~x:+81-.
1.
V93-t-3363Keyword:M.
ulti-Sc.
lc.
SymbolicDescription.
Pro-loinConformation.
Long-rangebt.
tcraction.
Pri-maryCon.
~tvo.
iTd.
~'.
StochasticModel.
S'uprtT~os!
dStochasticProJilc.
3D-IDalignmentIntroductionWithtimrecentl'apidincreaseinthenmnl)erofknown3Dproteinstructures,more~Uldulorerc-sc~u-chcrthinkthatthemethodtoithmtifypro-tcinsequencesthatfohlinto~known3Dstructurewonhlbcmoret)romisingthanthe3Dstructuret)rc(lictioll.
binitio.
Theinverseproteinfl)hlingl)roblcmhasbeenattractingalotofrescar('hersandmanyt)almrshavet)C(~llpublishedonthisis-sue.
ThisischictlyI)ccauscofChothia'sshock-ing(Icclarationthat""17u:vcwouldbe:v.
om.
orcthantho',.
sandproteinflt.
m.
ilics!
'"(Chothia9l).
InanynlcthodfortheI)roblcln,somekindofs('oringfimc-tionisdefinedtocwduatetlwfitofallamino-acidsequence(1D])eillg)tot)rotcil~confl)rmationslining).
Todefineone.
somefocused1)1|theCOlll-patibilityofeachamino-acidtypetothecnviron-mont~roundtheresidue(Bowieetal91),someontheeml~iricall)otentialderivedfi'omtheknown3DI)rotcinstru('ture(Sipt)landWeitckus92),314ISMB-94From:ISMB-94Proceedings.
Copyright1994,AAAI(www.
aaai.
org).
Allrightsreserved.
otherontilestatisticalpotentialbasedonBayesianprinciple(Goldsteinetal94).
SinceIfoundweakbutmeaningfulrelationshipsbetweenthetypeoflocalstructureofvarioussizesandtheprilnarysequenceatthatregion,IbegaaltoinvestigatetheapplicabilityofthcMulti-ScaleStructureDescription(MSSD)sehelnetothein-vel~sefohlingproblenl.
AnMSSDrcpresentsapro-teinconformationatmultiplescalelevels.
Ateachlevel,theconformationisdescribedbyasymbolicsequence,cachsymbolofwlfichdenotesatypeoflocalstructureofthelevelscMc.
Localstructurt~sareclassifiedintoseveraltypesateachlevelre-spectivelyaccordingtotheirshapeandthcenvi-ronnlent.
Theclassificationis,therefore,closelyrelatedtothesecondarystructuresparticularlyatthesnmllscalelevels.
Thedescriptionatnliddlescalelevelisconsideredtorepresentthesupersec-ondarystructures,andthatathighlevelsrepre-sentstheglobaltopology.
SinceIclassifiedthestructuresaccordingnotonlytotheirshapebuttotheirenvironment,twostructureswithsimilarshat)esbutinthedifferentenvironmentsareclas-siftedintodifferenttypes:thehelixexposedtothesolventisclassifiedintoadifferenttypefromthoseburiedinthenxolecule.
Letusc'M1thecompatibil-ityofthestructuretypetotheaminoacidsequence"primaryconstrMns"whichweregardasthecon-stralntsfromtlmprinxarysequencetothechoiceofstructuretypes.
Hence.
givenaualninoacidse-quencefragnlent,wecanroughlyestimatewhichtypeoflocalstructureitwouhlforln.
The3DstructurepredictionnxcthodbasedontheMSSDschemeisdiscussedintheliterature(Olfizukaetal94).
ToapplytheMSSDschelnctotheinversepro-reinfoldingproblem,theprimaryconstrMntsareusedinversely.
Givenafragmentofamino-acidsequence,wecanevaluateitsfittothestructuretypesofthefragments.
Orrather,givenastruc-turetypeatalevel,wecanobtainananfino-acidsequenceprofileattachedtothestntcturetypeun-dernlynlodel.
Thefitofagiwmamino-acidse-quencetotiffsprofileis,therefore,equivalenttothefittothestructuretype.
Sincethestructuresareclassifiedaccordingtotheirshapeandenviron-ment.
myapproachis,insomesense,theextensionofthemethodproposedintheliterature(Bowieetal91),wherethecompatibilityofananfino-acidsequencetothesecondarystructuretypeandtheenvironmentaroundeachresidueillthesequenceisconsideredtoevaluatetilefit.
Tileextension,here,indeedconcernsthemultiplescaleevaluationofthefit.
Thesequenceprofileiscalculatedbysuperpos-ingallthesubprofilesderivedfromtilestructurefragmenttypesinthegivenMSSD.
Thefitofase-quencetothewhole3Dstructureisnotonlyeval-uatedatthesnlallscalelevelintileMSSD,butat'allscalelevelsavailable.
ChancesarethateventhoughagivensequencedoesnotfittoaMSSDatlowlevels,thesequencemaywellfitathighlevels.
Thus,wecanidentifyasequencethatfoldintoanunknown3Dstructurebutsimilartoaknown3Dconformation,eventhoughthelocalfinestructuresoftheunknownonewouldbequitedifferentfromthoseoftheknownone:thefinestructuresmay(liftereveniftheamino-acidsequenceofthetwoproteinisverysimilartoeachother.
MethodThissectiondescribestilemethodsusedillmyinverse-foldingschenm.
Thefirstsubsectionil-lustratesthetechniqueappliedtothestructurefragnlentclassificationatvariousseale~s.
Thesec-ondsubsectionshalldefinetheprimaryconstraintsbetweenthestructuretypesandthet)rimaryse-quencefragments.
AndthenIformalizesthescor-ingfunctionfortheinversefoldingproblem.
Thelastsubsectionshallillustratethedynamicpro-gramnfingwithA*algorithmappliedtothealign-lnentbetweenthesequenceprofilederivedfromthe3Dstructureandtheanfino-acidsequence.
ClassificationofStructureFragmentsTheclassificationofstructurefragmentsisthenmstcrucialpartofnlyinverse-foldingscheme.
Agoodclassificationmayproducegoodresultswithhighdegreeofaccuracy.
Inordertoincorporatetherelationshipbetweenalargestructureflag-mentandtheprimarysequenceatthatregiomwehavetoclassifynotonlythesmallstructurefragnlcntsbutlargeones.
Howevertheclassifica-tionofthoselargeonesisdifficultwithoutsometechniquetoabstractthestructurebecauselargestructureshavemanydegreesoffreedom.
Iover-camethedifficultybyintroducinglineartransfor-mationofstructurefragmentintofixednunlberofnumericalparameters.
Here,thefixednumberofparanletersareextractedfromthestructurefrag-nlentsofanyscale,andthen,theyareclassifiedintoseveraltypesbysophisticatedclusteringtech-niquesateachscalelevel.
Amongtheparametersrepresentingthestructurefragments,sonlerepre-sentthestructureshape,aaldothersrepresenttheenvironmentaroundthestructure,howthestruc-turefragmentisburiedintheproteinmoleculeorhowexposedtothesolvent.
First.
Ioverviewthetechniqueappliedtothepa-ralneterizationofstnmtureshape.
Thisisdetailedintheliterature(Onizukaetal93).
ThemIanlgoingtoillustratehowtoparameterizctheenviron-nlentaroundthefragments.
ThetechniqueappliedOnizuka315tothestructureclassificationwillbebrieflyillus-trate(l.
Finally,Iwillbeshowingthedescriptionexamplesofproteinstructureusingtheclassifica-tionatmultiplescales.
TopologicalParametersInordertorepresenttilt;shapeofstructurefraglnentswithsmallmun-herofparameters,Iappliedliuem"transfo,wlatio.
ntothecooTdinaterepresentationofastruct.
u.
rcfrog-merit.
Thesetofexpansioncoefficientsobtainedfl'Olnthetransformationturns()tittol)e,afteraslightmodification,tilesetofparametersrepre-sentiugitsabstractedshape.
Wecanrestrictthelmml}eroft}aramctembychoosingacut-offorderintheexpansion.
ThistralmformatimlshallnotloosetheimportantfeatureofthelargestructureI}{~auscthesignificantcoe]~icientsusuallyappearatthelowerordersinthelinearexpansion.
Thecut-off,here,isequivalenttotheneglectoftheuse-lessinfonnationontheshN)eathigheror(lets.
kStructurefragmentwith5residuesOriginPositionalVectorsweightedbytp~.
.
1~484.
.
/:,':~ii',%,J{,SoFigure1:AbstractionofStructureFragmel,tThet)rocedureofthel}aranmtcfizationinvolvessevcrMstepsasfollows.
First.
asetoforthonor-lnMbasesforlinearexi)ansionisi}rovided.
Sec-ond,thesetoftopologicalvectorsiscalculatedastheabstractedformofastructurefraglnentbylin-earlyexpandingthecoordinatercprascntationofthefragment.
Thenwcextrax:ttheorie.
lktationin-variantparametersfrolnthesetoftopologicalt)a-rameters.
Finally,wedefineaparityparameterthatdiscrilninatethemirrorimages.
Thesetofbasesforthelim.
'arexpansioninthisstudynmstbeorthonormalinthediscretesystem.
Aspecialsetisthusrequired.
Oneofthesimplest316ISMB-94setofI)asesisdefimxlbypolynomials.
LetNbethenmnberofCOnlponelltsoftileI}a~se.
LetC2N.
~.
,denotethe.
ithColnponcntofthcbaseofkthor(h.
'r.
Thisissimplydefinc.
dbyakthorderl)olynomialofx.
~ON.
ki=VO~v,k(zi)=e+c~:r,+r2x~+ca:rai+.
.
.
+ckx~.
Theorthonorn,alcon(littonforthissetis.
N-IN.
ji~oY.
~,.
,jI,:i=o(l}N-~):1=(~o~,-.
~,i=0LetSidenotethepositionalvectorrel}re.
sentingthepositionofithresidueinastructurefragment.
ByoperatingtheorthonornmlI}a~eqON.
k,totheseriesofthepositionalvectorsSi.
wecanobtainatopologicalvectorT~astheexpansion(:oeffici{mtsofthelinearexI)ansion.
N-1Tk=~_,~N,kiSi.
(2)i=1}Thesetoftopoh)gicalw~ctorsareth{'abstractedformthefragment.
Col~sideringthepropertiesoftheI)~sesusedto('alculatethesevectors.
T~rel}-resentsai)proxinmtelytheabstra,:tcdlengthofthestructurefraglnent:T2representsapl)roxinlatclytheatxstrax:t{,(Icurvature;T3obviouslyrei)resentsthetwi~t:T4representsthemeaudel'.
ThedirectionofthetOl}ologicalvectorsdependsontheabsoluteorientationofthestructurefrag-meat.
Wehavetoextracttit{;orientationiuvariantl)arame.
tet>.
Inaddition,wenee{1to(lefincapar-ityparametertodiscriminateOllefrontitsmirrorimage.
Hence.
elevenparametersarerequiredtorepresentastructure:fourforthehmgthoftoi}o-h)gicalve('torsITilsixfortheM)solutcdifferencebetweenthetwovectm~IT,-Tjlandonefortheparity.
Theparityl)aramctertakessuchavalueasfollows.
Thesignoftheparityparameterofastructureisdifferentfrontthatofitsmirrorlinage.
Ifthesignisnegativeforastructure,l}ositiw'isthesignforitsmirrorimage.
Thei)ltensityofthepality1}aramcterisslnallwhenthestructureisnearlysymmetric,whilelargeisitwhenstronglyasymmetric.
Wecanobtainsuchat)arameterbycalculatingthevectorproductoftopologieMvectors.
Idefinedtheparityparalne.
terPas({(T1-T2)*(T~T3)}.
Ta-Ta)/L2.
whereLisaconstantspecifictothescaleofstructure,whose.
(limensiouisleugth.
Lisdefinedasthemeanlengthoftopoh}gicalvec-tors.
Hence.
thedimensionofallthetopologicalt)arametm~istheleugth.
EnvironmentalParametersHere,Idiscusshowwecan1incorporatethesolventaccessibilityofstructurefraglnentsintothestnlctureclassifica-tion.
Moreaaldmorebiologistsareawareoftileim-portanceofhydrophobicinteractionbetweentheresidues(luringthefoldingprocess.
Aproteinchainsofoldsintoatertiarystructurethatthehydrophobicresidueswouldbeburiedinsidethcmolecule,whereasthehydrophilliconesexl)osedtothesolvent.
Thehydropathyofeachresiduemustbeastrongfactordetenniningtheenvironmentaroundtheresidue.
Whenastructurefraglnentisdeeplyburiedinthemolecule,mostresiduesillthefragmentshouldbehydrophobic,whilehy-drophillicwhenexposedtothesolvent.
Indeedisitthat,whentilefragmentishalfburiedandhalfex-posed,theresiduesaroundtheburiedregionshouldbehydrophobicandotherresidueshydrophillic.
Thepropensityofeachaminoacidtypetotheell-vironlnentisconsideredevenstrongerthanthattothesecondarystructure(Saitoctal93).
Consid-eringtilepropensityfromtheprimarysequence~wecallestimatehowthcthestructurefl'agmeutwouldbeburiedorexposed.
Illordertochar-acterizetheenvironmentaroundastructurefrag-ment.
Iintroduceanewparanmtcrattachcdtoeachresidueillthestructure,theQuasiBuriedDepth(QBD),whichtakespositivevaluewhentheresidueisburiedinsidethemoleculewhiletakc~negativevaluewhenexposedtothesolvent.
Thedimensionoftheparameterislengthsothatthccalculationwiththetopologicall)arametersphysi-callywouhtmakesense.
First.
IgivethedefinitionofQBD,andthenIillustratehowtoparameterizethesolventaccessibilityofastructurefragment.
Aresiduedeeplyburiedinsidethemoleculeissur-roundedbymoreresiduesthanthoseexposedtothesolvent.
Thenumberofresiduesnearbyagivenresiduewithinacertaindistancecanbeconsideredtomeasurehowtheresidueisburiedorexposed.
Thisnumberisgivenbycountingthenulnberofresiduesillaspherewithcertainradiuscenteredatthepositionofagivenresidue.
Thepredictabil-ityofthisnumberfromagivenprimarysequenceisdiscussedintheliterature(Saitoetal93).
TheQuasiBuriedDepthisderivedfromthenmnl)er.
andhastiledimensionoflength.
FromtheinvestigationoftilelnmxinnunnunlberofresiduesMinaspherewhoseraxliusisr,IfoundthatMisalmostproportionaltother2"45,andiscalculatedasM=0.
15r2"45.
Thissuggests,theresiduesarenotoptimallypackedbutarcsubop-timaUypackedinthesenseoffractaldimension.
WeCallconsiderthatwhentheactualnumberofresiduesNinthespherewithradiusrcenteredatagivenresi(hmw(nfldI)eequaltoM,tiledepthfromthesurfaceoftilel)roteinlnoleculetotileresiduewouldbeestimatedgreaterthanr,whilethedepthwouldbee~stimatedaroundzerowhenNisahalfofM.
ThenulnberNcanbc,therefore,transformedintothequasidel)thoftheresiduefromthesurface.
TheQuasiBuriedDepthdQis,therefore,calcu-latedasdQ=(2N/M-1)'r,whereM=0.
15r2'45.
WhendQtakesapositivevalue,theresidueiscon-sidcredburied,wlfileconsi(teredexposedfortheuegativedQ.
Likewisethetopologicalparameterswhichareol)-taine(lbylineartransformation,thesetofenvi-ronmentalparametersrepresentinghowastruc-turefragmentisburiedorexposediscalculatedI)ytrzmsformingthesetofr~i(lues'QBDillastruc-turcfragment.
TheenvironmentalparameterofkthorderE~iscalculatedasbelow.
N-IEk=~~N.
k~d,(3)i----0wlwrcd~2istheQBDofithresidueillthefrag-meut.
Sincethephysicaldimensionofenvironmen-talparametersislength,theseparametersCallbeusedwithtopologicalparameters.
Illmystudy,thenlaxinmmorderofexpansionisfive,andfiveenvi-roulnentalparametersaretorepresentthesolventaccessibilityofthestructurefragment.
ClassificationofStructureFragmentsThestructurefragmentabstractedandrepresentedwithafewt)arametersmaybeclassifiedI)3,aclus-teringtechniques.
IadoptedLeaningVectorQuan-tization(LVQ).
LVQclassifieseachdataillthedatasetaccordingtothenearestccntroidtothedata.
ThedistancebetweentwodataDisis,inmystudy.
definedtheEuclidiandistaalcebelow.
D~j=i~_,(Ti,~-Tj,k)2,(4)whereTi.
kisthekthcomponentoftheithdata.
ThecentroidsfortheclusteringhereareobtainedI)ytheiterativeprocessasfollows.
Theinitialccn-troi(lsarearbitraryplacedillthen-dimensionalspacewherenisthenuml)erofcolnponentsofthedata.
Eachdatainthesetisclassifiedaccor(lingtothenearestinitialcentroidtothedata.
Bythisinitialclassification,thedatasetisclassifiedintotheclustersrepresentedbyeacheentroidrespec-tively.
Eachcentroi(linthenextstepiscalculatedasthemeaalofthedatabelongingtothecluster.
Thenthedatasetisagainclassifiedaccordingtothenewceutroids.
Tiffsprocessisiterateduntilthedifferelwcbetweenthepopulationofea~llnewclusterandthatofpreviousoneislessthan2%ofOnizuka317thepolmlatiomwhenIconsiderthatthepositiouofeachcentroid~hllostCOllVel'ges.
Scale012312997654933251713975CCCCCCCCCCABBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBCCNNNNNOOCCCCCJJJJJJOCCCCCCCCCCCCCCEJJJQQQ0qQOqQOJJLLLLCCCCCCLLCCCCCCCGFFFCJJOqJJLLLLLRRRRRJJBBBBBBBBBBFFGOOOPPPPPGGGEEHHHJJJJJJLIIKKKKKKUUUAACEELLLLLLLLLFFFBBJJSSSSRKIBHHHIIIPCAGGGKKKKKKKKKKKDDDAIOUUUULHHIIMMLWULMABIIIIOOOOOOIGGGGBBHHTTTTHLFFFHWUUUNEEPKOOOOOOOOOOGGGAEJLQQQQLDAFFWWWVSQJOLEMMMMMMMMMMEEDAJFPPPPPSJDADSSP-eeeee-ssshhhhhhhhhhhhhhhtt---eeeetSeq.
MKIVYWSGTGNTEKMAELIAKGIIESGKDVNTINVScale45612997654933251713975BBBBBBBCBBBBBBBBBCCCCCCCCCCCCCCCCCCCCCCCCBCCCCCCCFFFEEEEEEEEJJJJFFFCCCCCEEECCFFFIIIIIIJJJJFFFEELTTWWWQPJEBBFFFFBUUUWTTTLLLCACIKKKRRRSJJJJJJEEEHHUUUEHHOOOTWWWVKKDDDFFFIMIIIIMMMMMIGEEEMMEGBOOOVSXWWRCCCCBEJJEEEEJJJJJJMMEHFDDEEBNOVVVXXUULAACCHRLABEDDDDDDDDHDCBBBFCMMVWXXXUUSDEECLLNEABBGBBBBBFIHABAAAFOLWWWXXVVSJJDLQNJBBCDDAAABDSSPtt--sttttt-seeeeee--btttb--ttthhhhhSeq.
SDVNIDELLNEDILILGCSAMGDEVLEESEFEPFIScale7890129976549332517[3975BBBBCCJJCEEEEEEEEENNFFFFBBBIIIHONGGGGFFCIIJQqPPPPLLLLLSSSTOUXXTUMMMCCCFFFJRRRRRIIEEEHHHHQOQNNLO000WTTTVKKAAAGGMMMMMMMMFFIIHEGJORRLGIOOSSXXWRRCCCBEEJJJJJJJJJDDEEDILODFFQQNNVVXWWUULACCQEEEGGGGEEGEEBBHTBBFFJFPRWWWWXUUSDEJMGGKGGGBGGBBGICMAADBFFBLTWWWWXVVNKFOOLCEDGCEDGCDDBODSSPhhhstt-tt-eeeeeeeesss-shhhhhhhhhhhhSeq.
EEISTKISGKKVALFGSYGWGDGKWMRDFEERMNGScale12312997654933251713975QLLACEFA(KKRRRRKKKBBBHHHMMMMUUUUUUPHCCDDIGGJJJKKJRMLQQTWRMMMMBFEEEEIIIIIGGUULNMRRWUSNNNAACMKKKKKKKKGGLSSNJOOTWSQQONABBFDGEEGGEEGCADSSPtt-ee-s--eeees--ggghhhhhhhhhhhht-Seq.
YGCVVVETPLIVQNEPDEAEQDCIEFGKKIANI318ISMB-94DescriptionExamplesThedatasetusedinthisstudywastakenfromtheselectedpro-teinstructuresofProteinDataBankbyEMBL(Hobohmetal92).
Fromtheselection.
Ifitrtherselected245structuredeterminedbyX-raychrys-tMlography.
Thesequencehomologyl)etweeneachpairofproteinchainsisalwayslessthan25%.
TheradiusofspheretodeterminetheQBDis11)~.
ThedatasctatN-residuelevelisobtaiuedbycalculatingtilesixteenparametersofallpossibh,'structurefragmentswithNresi(lm~inallthese-lccte(lproteinchains.
Iclassifiedthestructurefragnlelitswith5.
7.
9,13,17,25.
33,49,65,97.
129,aml193residuesandobtaiuedthetwentyfourtypesateachscale.
ThelettersfrolnAtoXdenotethestructuretypes.
Thecouformationof4FXN(Flavodoxin)is(k~cribedinthisschemea.
~above.
Thelinesat"DSSP-denotethesccon(larystruc-turesa.
~signedbyDSSP.
Atthe5-residuelevel,thesitesymboledA.
E,G.
orMusuallytakcshelicalconformationdenotedbyh,andthoseofV.
WorXusuallytakestrandsdenotedbye.
Thestru('-turetypesattim5-residuelevel,therefore,well(:or-r(,'spott(Itosecoudarystructures.
Thedes(~ril)tionathighlevc,lscani)econsi(lcredtorepresentsu-perseronda'tT]struchw(',s,andthoseatthe65or129-residuelevelwouhlcorrespondtothesomedoma'in.
sorgh,balstructm'e~s.
Wecan,'oneludethattheMSSDpreciselyrepresentsthehierar(:hi-calprol)extyof3Dproteinstructure.
Inthisway.
aproteinconformationdescribedinthismulti-s('alestructure(lescriptionschenwshowshowtheconformationisbuiltUl,ofthesubstruc-turesandstructuralmotifs.
PrimaryConstraintsTilt:primarycoustr~iutsrelatetheprimal~se-(luenceandthestructuretypeateax:hregiou.
MSSDschemeist)articularlysuitat)letomodelbothh)ealandglol)alfactorsofstructure,h)rma-tion.
The1)rimaryconstraintsfl)rshortstructurefragnmntsnatundlyrepresentlocalfact()rs,andthoseforhmgon(,'srci)resentglobalorlong-rangefactors.
Forhlrtherdiscussion,Idefineseveraluo-tationshere.
Let7~(lenoteastructuretype,whereimrinally71k=Ak,7~"=Bk.
.
.
.
.
~ff6=pk.
Letc~k,lenot,,aprimarysequencefragmentattilekthlevel.
An(1wefllrtherdenote.
wka~thenumberofresiduesinthestructurefi'agmentattilekthlevel.
WedenoteF~"E{AI',Bk.
.
.
.
.
X~}asthevariablethattakesastru(:turetype.
wherei(leuotesthepositionthel)rimarysequence.
WealsodenoteE~astilt,,variablethattakesaprimarysequencefragntent.
Notethatthepositiollihcredenotesthepositionofthefirstrt,'shlucoftilestructurefragmentinthe,prilnarysequence.
Theprol)M)ilityofaprimarysequencefraglnentakformingatypeofstructure%~"isrepresentedaspp(r~_k,~k=ak="ltli).
SinceweassumethattheprimaryconstraintisinvariantofitsM)solutepositionilltileprimarysequencebutonlydependsoutilestructuretypeandtileprimawse(luenceatthatregion,itlnaysilnplyt)erepresenteda.
spp(r~lzk).
Inthepreviousliteratures(Onizukaetal93:Onizukaetal94).
Idefinedgeometriccon-straintsbetweentheoverlappingstructurefrag-ments,whichisessentialfactorfor3Dproteinstructurepredictionabinitio.
Inthispaper,Idon'tdiscussonthisissuebecausetheyhavenothingtodowiththeinverse-foldingschc,ncusingMSSD.
InthefieldofmolecularbiologT,thesequencepro-filesarefrequentlyusedtoanalyzetherelation-shipbetweenasequencepatternandthestructureorfunctionatthatregion,wherethefrequencyofeachamino-acidtypeiscountedwithr(~l)ccttotheposition.
Thistechlfiqueisdirectlyappli-cabletomodeltheprinlaryconstraintsatsmallscales,thoughitrequireslargelmmberofparam-eters,again,fortheprimaryconstraintsatlargescale.
Forcxamplc,atfive-residuelcvel,thenum-berofparalnetersrcpresentingthefrequencyis100=20x5where20isthenumberofaluilm-acidtype~,and5istilenulnl)erofresiduesilltilestructurefragmentatthatlevel.
Atthelargescalelevels,wherethenumberofresi(luesaremorethan100,nmrethan2000parametersarerequired.
Inthiscase.
however,wecancomt)resstheseqummcprofileusingthesametechlfiqueasIappliedtothestrm:tureal)straetion.
Wecanalwaysreducetilexmnlberofparametersinto100usinglinearCXl)aal-sionagain.
Inverse-foldingSchemeGivenanMSSDret)rescntinga3Dl)roteinstruc-turc.
wecanestinlatcthemostprobablesequencefi'omtheMSSDusingtheinverseprimarycon-straintsPI(EIF),whichissimplygivenbycalcu-latingtilefitofase(luencetoaprofile.
Pp(FIE)iscalculatedbyai)i)lyingthepriorP(F)toPI(EIF).
Letidenoteapositioninthesequence.
LettAdenoteallamino-acidtype.
~ndletTAbeavari-al)lethattake~oneoftheaminoacidtypetA.
WeCallderivetheprobabilityP(TA=tA)oftheanfino-aeidtypeoecun-iugatthepositioni,fromtilestnmturefragmenttypecoveringthepositionAAi.
LetPI(Ti=t]['j)denotetheprobM)ilitythealnino-acidtypetAoccurringatthepositio,tiinthefragment.
TosuperposethePI(TA),wehavetodividethisvaluebythepriorP(TA=tA),becausetilepriorisdoublyortriplycalculated.
Thus,PI(TA)iscalculatedasbelow.
p(TA----tA)=p(tA)PI(TA=talrJ)P(tA)AllP1~overinffi(5)Inthisease,however,thepriorP(tA)doessome-tiringunpreferable.
TheprobabilityP(Tff=tA)almostalwayssuggeststhatAlanineistilemostprobableamino-acidtypeatallyposition.
Thislneemsthattheinversel)rilnatTconstraintPI(TAIEj)ismuchweakerthantheprior.
Hence,IadoptC~(Tff=tA)=Pt(Tff=tA)/p(tA)in-steadofPx(TA=ta).
Thisvalueisgreaterthan1.
0whentheamino-acidtypestochasticallyoccursmorethanrandomlevel.
Thesuperpositionof'alltheinverseprimal5,con-straintsfromtheMSSDderivedfi'onlthegiven3Dstructureyieldsastocha,stiesequenceprofile.
Thefitofasequen('etothisprofileisconsideredthefittothegivenconformationrel)resentedbytheMSSDandl)yturnthefittothegiven3Dstruc-ture.
3D-1DAlignmentThealiglunentbetweenthese(luenceandthepro-fileiscarriedoutsimplybydynamicprograulnfing.
Thedynamicprograumlingsearchesfortheopti-ur,flalignmentthatminimizethescoreEbelow.
Someal)t)rol)riategappenaltyshouldbeusedwheuwel)ernfitgaps.
=-ElogCI(TiA=tA)+9appen.
alty.
(6)EiWeconsidertheresultantscoreEasthefitofamino-acidsequeucetothcsequenceprofileCI(TA)derivedfromtheMSSDrepresenting3Dstructure.
Hence,giveuaprimarysequenceofaproteinwhose3Dstructureisunknown,wecansearchforthcmostcompatible3Dstructureintheproteiustructuredatabase.
ThisisfarsimplerthanthatofthoseschenlesusingSipplpotential(SipplandWeitckus92:Jonesetal92;YukcamlDill92;SkolnickandKolinski92),whereitisnecessarytoapplythedoubledynamicprogralnnfingthatre-quireslargeamountofcalculation.
IappliedtheA*algorithmtotile3D-1Dalign-meut,whichwasfirstappliedtotheproteinse-quencealignmentintheliterature(Arakietal93).
Thisalgorithmfindstheoptimalsolutionwhilethecalculationamountisnmchsnlallerthealthatofeonveutiona,1dynanficprograanmingalgorithms,thoughtheinlplcmentatiouismuchdifficult.
Thechoiceofthegappenaltyhasnotyetestab-lished,himostcases,therearethreeparame-tcmconcenfingthegappenalty:1)theslidegapOniznka319penaltyisthe(:()stforthcoffsetI)etweenthesequence;2)tileinitialgappenaltyisthecosttoputagapinasequence:and3)theincrementalgappenaltyisthecostfortheh;ngthofeachgap.
Whcntheinitialgappenaltyequalstoincrcnmll-telone,the(lynanficprogramnfingturusouttobequitesimplewithasimplenetwork.
Thus,Iadoptedthispcnalty.
Theslidepenaltyshouhlbezerotoallowanyoffsetbetweenthesequenceandprofilewithoutcosts.
ResultsIusedthesamedatasetoft)roteinstructuresa.
sthatusedforstructureclassification.
Tocross-validatethe,result,thedatasetwasdividedintofivegroupsrandomlysothateachgroupwouhlcon-tainfortyninestnlcturcdata.
Iobtainedfivesetsofp1~maryconstraints,whereeachsetwasderivedfromthestructuredatainfivegroups.
Whenastructureyieldsthesequenceprofile.
Ididnotusethoseprimaryconstraintsthatarederivedfl'omthestructuregroupincludingthatstructurc,.
First,asal)reliminaryexperiment.
Iinvestigatedhowaproteinsequencefitsitsown3DstructureevaluatingtheZscore.
Here.
Ididnotaligntheprofileaadthesequence:thegapsarc.
thus.
notconsidcre(I.
WecanobtaintheZscoreofase-quencctoaprofilebynormalizingthescoreEbythemeanscoreall(Ithe(levia-tionCrEr,,,a.
.
.
.
ofraa~(lonlS(Xluen(:estothatprofile.
whereEisdefineda.
sbelow.
-ElogC1(7~A=tA).
(7)EiThus.
ZscoreEzis,E-(ErandomEz=(8)CIEr,,.
doraIinvestigatedthefitofse(luencestothestnlcturesatonlyOllescalelevel,inordertoseewhichh;velbestcorrespondsthesequence.
TheplotbelowshowstheineanZscorewithrespecttothescalelevel.
Thecorrespondenceisthebestatthelow-est5-residuelevelandit(lecrca;seslnonotonouslywiththeincreaseintilt;level.
Thissuggeststhatalocalsequencestronglyinfluencethefonnationofthesecondarystructuresatthatregion,becausetheclassificationatthe5-residuelcw;lwellcorre-si)ondsthesecondarystructures.
Probablyduetotheover-learning,thescoresatthehighlevelsarebelowzero.
Second.
IcheckedwhetheraseqUellCewouhliden-tifyitsownstructurc.
Thchit-ratiooftheself-identificationdirc('itysuggeststhet)erfonnan('cmyinversc-fi)ldingschemc.
Icl.
eckcdwhetherthefitofasequencetoitsownstructurewouklscorcs320ISMB-94\\i.
.
.
.
.
.
:oScale(NumberofResiduesin"Fragments)Figure2:ZScorevel~usScalethc,bestamongallsequence-profih:combillations.
Wcselectcd188proteinstructuresfromthedatasetwhichIusedtomodeltheprimaryconstraints,becausetheotherstructuredatacontainresi(hm-lacksorunacceptablebondlengths.
Iinw'st.
igatedthehit-ratioofself-identification.
Whenthe('onl-patil)ilityscoreofthesequencetoitsownstruc-tureobtainedfromthe3D-1Dalignments('orcsthebest.
Iconsiderthattheidentificationhits.
Ididexhausting3D-1Daligammntfor188*188times.
Thetal)lcbelowshowsthehitratiom~s.
ITotal[Hit]HitRatioISingleLevel188630.
335[Multi-Leveli88900.
478IThisresultactuallyshowsthatthepel'formanceofself-identificationisbetterwhenmanyscalelevelsareincorporated.
HitRatioiii.
.
:.
4.
GapPenaltyFigure3:HitRatioversusGapPevaltyThirdIinvestigatedhowthegapl)enaltyinflucn(:ethehitratio.
Inthiscase,Iusedonlyfirstgroupofdatasetwhichcontainsthirtynineproteins.
Thisgraphshowsthattilehighertilegappenaltyis.
tilebctteristhehitratio.
DiscussionInthispaper,Iproposedthenndti-scaleevaluationschemetosolvetheinverseproteinfoldingprob-lem.
Iincorporatedtheconq)atibilityofsequencesto3Dstructuresnotonlyatthesmallscalelevelbutalsoatthelargeseal(;levels.
Theresultsshowthatthemulti-scalecompatibilityscoringworksbetterthanthesinglescale()ale,eventhoughthecompatibilityscoresatlargescalelevelspoorlycorrespondsthefitbetweenthestructuresandsequcncesbetterthanthoseatsnlallscalelev-els.
Consideringsizcofdatasetcontaining188proteinstructures,theresultisnotsobad.
Oneofthedifficultproblemsunsolvedishowwecaaldetel'minethegapl)enalty.
AsIshowedthehitratioversusgappenalty,thehigherthegappenaltyistilebetteristhehitratio.
Iuthissense,forthebetterperformance,thegappenaltyshoudbehigh.
However.
thehighgappenaltydoesnotper-mittherobustidentification.
WhycanweinsertgapsinthealignmentsThegapsinastructureInaychangethestructure,andthen,thedifferentenvironmentmaybeformed.
ThelengthofexteriorloopsofaI)roteinstructureisvariable.
Eventhemainchaintopologylooksalike.
Wehavetopermitthegapsintim3D-1Dalignment.
However,therobustidentificationbyturnproducesworseself-identificationhit-ratio.
ConsideringthepoormeanZscoreathighlev-els,the3D-1Dcorrespondenceathighlevelsdoesnotseemtobestochasticallylnodelabie.
Thus.
wcshouldnotusethoselevelsinordertoobtainbetterself-identificationhit-ratio.
IinvestigatedtheapplicabilityofMSSDschemetotheinversefoldingproblem,andfoundthatthenlulti-scMescoringworksfarbetterthansin-glescalescoring.
Thismeansthatthescoreathighlevelsdoesagreatdealtoenhancetheperfor-nlance.
ReferencesOnizuka.
K.
;K.
Asai;M.
Ishikawa;andS.
T.
C.
Wong1993.
"'AMulti-LevelDescrit)tionSchemeofProteinConformatioll".
P'roc.
ofISMB-93:301-310.
CyrusChotlfia1992.
"Onethousa~Mfamiliesforthemolecularbiologist".
Nature357:543-544.
Bowie.
J.
U.
R.
Liithy,andD.
Eisenberg1991.
"AMethodtoIdentifyProteinSequenceThatFoldintoaKnownThree-DilnensionMStructure"SCI-ENCE253:164-170.
Sil)pl,M.
,andS.
Weitckus1992.
"DetectionofNative-likeModelsforAminoAcidSequcnees".
PROTEINS13:258-271.
Goldstein,R.
A.
,Z.
A.
Luthey-Sclmltcn,andP.
G.
Wolynes1994.
"ABayesianApproachtoSe-quenceAlignmentAlgorithmforProteinStruc-tureRecognition".
Proc.
of27thHICSS5:306-315.
Onizuka.
K.
.
K.
Asai.
H.
Tsuda,K.
Ito.
M.
Ishikawa.
andA.
Aiba1994.
"'ProteinStructurePredictionBasedonMlflti-LevelDescrit)tion".
P~vc.
of27thHICSS5:355-354.
Saito.
S.
.
T.
Nakai,andK.
Nishikawa1993.
"'AGeonleticalConstraintApproachforRcl)roducingtheNativeBackboneConformationofaProtein".
PROTEINS15:191-204.
Hobohm,U.
,M.
Scharf,R.
Schncider.
C.
Sandcr1992.
"Selectionofarepresentativesetofstruc-turesfromtheBrookhavenProteinDataBank".
ProteinScience1:409-417.
Jones,D.
,W.
Taylor,andJ.
Thornton1992.
"'ANewApproachtoProteinFoldRecognition".
Na-ture358:86-89.
Ynke,K.
,andK.
Dill1992.
"InverseProteinFold-ingProbleln".
Pivc.
Natl.
Acad.
Sci.
USA89:4163-4167.
Skolnick,J.
.
andA.
Kolinski1992.
"'TopologyFin-gcrprintApproach".
Science250:1121-1125.
Araki,S.
,M.
Goshinla.
S.
Mori,H.
Nakashima,S.
Tomita,Y.
Akiyama.
andM.
Kanehisa1993.
"'Ap-plicationofParailelizedDPandA*AlgorithmtoMlfltit)leSequenceAlignment".
Proc.
ofGemomeInformaticsWorkshopV:94-102.
Onizuka321
o-ku,Tokyo,108Japanonizuka@icot.
or.
jpPhone:-t-81-3-3456-3192,Fax:+81-3-3456-1618KiyoshiAsaiElectrotechnicalLaboratory(ETL)1-1-4,Umezono,Tsukuba,Ibaraki,305Japan~ai@etl.
go.
jpFax:+81-298-585939AbstractTimapplicttbilityoftheM'ulti-Sc,lcStr.
uctuveDc-.
~criptiou(MSSD)schcm.
ctoth.
ci,.
ecvsc@ddingpcobl,m.
~wasinvcstiyatcd.
A,.
MSSDvcprcsc.
lt.
t.
~ct.
/Dproteinstvm'tu'rcwithmultipb:symbolicse-qlte:/t('c.
%II,/le:7"ctin("setact.
arcsm'~:rcprcsc.
n.
tcdwithth.
c.
~cqtu:ncce,tlowlevels,tlu.
m.
iddlcscalestruc-tm'n.
lm.
otif.
~a.
tm.
'iddb:Iwvcls.
a,d91obaltopologyathigh.
lc'pels.
Each.
symbolintit.
(:symboh:csc-qucuccdenotesatypeoflocalstructureofthelevelscah~.
ThestructurefragmcTtts,.
.
recl,.
ssificdatc,ch.
re:alelevelVeSl.
,ccth,elyacco'rdi~tfltoth.
cshapea~utthectt.
Trivonmcntarouttdthe:fragments:h.
o'tvth.
c.
struct'utvise:tTJoscdtotimsolre:heorb'uricdi,.
th.
r:mole.
cult.
Imodeledth.
c.
pvopc.
,.
sityofwn~rm.
iTto-acidscq'tzt:Tu'ctoth.
cxl.
r.
uctavcfcayTncttttype(i.
c.
.
pvimo.
ryconstraint)~tteachs,hh"m'l.
Th.
elocalpvopc.
n.
sityis.
therefore,m.
odclcdatsm,llscale(low)b"vcl.
~.
.
u.
,hilcth.
c.
qlob,.
lpr(qm,.
sity7nodelcdl,.
7~1cm',.
lc(high.
)levels.
Th.
us.
mqmtTmsi,9alltheprim.
a.
ryconstvai.
n.
ts.
,.
']DpvotciTt.
strm't,.
rc.
yiddsmtamino-acid.
sequence.
profile.
Ee',luatiTt9thefitofvna'mDtoacidscqm,.
cctotimprofih'dcri'm:dfrom.
theknown31)protci',,st.
r,.
ctuw'.
.
,u'canidcn-tz~f!
lmh.
ich3Dstr.
m'rm',theflivcttam.
ino-acidsc-quc.
'n.
ccwo.
,.
hlflddi,to,lch.
ccl,:('dwluth~ram.
'-1Currently~tMatsushitaResearchInstituteTokyo,Inc.
3-ll)-1tlig~himita.
Tama-ku.
Kaw~us~ki21.
t.
,btl)~UlE-Mail:.
uizuka:~,~mrit.
mci.
('o.
jl)hon(,:+81-.
1.
1-911-635I.
l";~x:+81-.
1.
V93-t-3363Keyword:M.
ulti-Sc.
lc.
SymbolicDescription.
Pro-loinConformation.
Long-rangebt.
tcraction.
Pri-maryCon.
~tvo.
iTd.
~'.
StochasticModel.
S'uprtT~os!
dStochasticProJilc.
3D-IDalignmentIntroductionWithtimrecentl'apidincreaseinthenmnl)erofknown3Dproteinstructures,more~Uldulorerc-sc~u-chcrthinkthatthemethodtoithmtifypro-tcinsequencesthatfohlinto~known3Dstructurewonhlbcmoret)romisingthanthe3Dstructuret)rc(lictioll.
binitio.
Theinverseproteinfl)hlingl)roblcmhasbeenattractingalotofrescar('hersandmanyt)almrshavet)C(~llpublishedonthisis-sue.
ThisischictlyI)ccauscofChothia'sshock-ing(Icclarationthat""17u:vcwouldbe:v.
om.
orcthantho',.
sandproteinflt.
m.
ilics!
'"(Chothia9l).
InanynlcthodfortheI)roblcln,somekindofs('oringfimc-tionisdefinedtocwduatetlwfitofallamino-acidsequence(1D])eillg)tot)rotcil~confl)rmationslining).
Todefineone.
somefocused1)1|theCOlll-patibilityofeachamino-acidtypetothecnviron-mont~roundtheresidue(Bowieetal91),someontheeml~iricall)otentialderivedfi'omtheknown3DI)rotcinstru('ture(Sipt)landWeitckus92),314ISMB-94From:ISMB-94Proceedings.
Copyright1994,AAAI(www.
aaai.
org).
Allrightsreserved.
otherontilestatisticalpotentialbasedonBayesianprinciple(Goldsteinetal94).
SinceIfoundweakbutmeaningfulrelationshipsbetweenthetypeoflocalstructureofvarioussizesandtheprilnarysequenceatthatregion,IbegaaltoinvestigatetheapplicabilityofthcMulti-ScaleStructureDescription(MSSD)sehelnetothein-vel~sefohlingproblenl.
AnMSSDrcpresentsapro-teinconformationatmultiplescalelevels.
Ateachlevel,theconformationisdescribedbyasymbolicsequence,cachsymbolofwlfichdenotesatypeoflocalstructureofthelevelscMc.
Localstructurt~sareclassifiedintoseveraltypesateachlevelre-spectivelyaccordingtotheirshapeandthcenvi-ronnlent.
Theclassificationis,therefore,closelyrelatedtothesecondarystructuresparticularlyatthesnmllscalelevels.
Thedescriptionatnliddlescalelevelisconsideredtorepresentthesupersec-ondarystructures,andthatathighlevelsrepre-sentstheglobaltopology.
SinceIclassifiedthestructuresaccordingnotonlytotheirshapebuttotheirenvironment,twostructureswithsimilarshat)esbutinthedifferentenvironmentsareclas-siftedintodifferenttypes:thehelixexposedtothesolventisclassifiedintoadifferenttypefromthoseburiedinthenxolecule.
Letusc'M1thecompatibil-ityofthestructuretypetotheaminoacidsequence"primaryconstrMns"whichweregardasthecon-stralntsfromtlmprinxarysequencetothechoiceofstructuretypes.
Hence.
givenaualninoacidse-quencefragnlent,wecanroughlyestimatewhichtypeoflocalstructureitwouhlforln.
The3DstructurepredictionnxcthodbasedontheMSSDschemeisdiscussedintheliterature(Olfizukaetal94).
ToapplytheMSSDschelnctotheinversepro-reinfoldingproblem,theprimaryconstrMntsareusedinversely.
Givenafragmentofamino-acidsequence,wecanevaluateitsfittothestructuretypesofthefragments.
Orrather,givenastruc-turetypeatalevel,wecanobtainananfino-acidsequenceprofileattachedtothestntcturetypeun-dernlynlodel.
Thefitofagiwmamino-acidse-quencetotiffsprofileis,therefore,equivalenttothefittothestructuretype.
Sincethestructuresareclassifiedaccordingtotheirshapeandenviron-ment.
myapproachis,insomesense,theextensionofthemethodproposedintheliterature(Bowieetal91),wherethecompatibilityofananfino-acidsequencetothesecondarystructuretypeandtheenvironmentaroundeachresidueillthesequenceisconsideredtoevaluatetilefit.
Tileextension,here,indeedconcernsthemultiplescaleevaluationofthefit.
Thesequenceprofileiscalculatedbysuperpos-ingallthesubprofilesderivedfromtilestructurefragmenttypesinthegivenMSSD.
Thefitofase-quencetothewhole3Dstructureisnotonlyeval-uatedatthesnlallscalelevelintileMSSD,butat'allscalelevelsavailable.
ChancesarethateventhoughagivensequencedoesnotfittoaMSSDatlowlevels,thesequencemaywellfitathighlevels.
Thus,wecanidentifyasequencethatfoldintoanunknown3Dstructurebutsimilartoaknown3Dconformation,eventhoughthelocalfinestructuresoftheunknownonewouldbequitedifferentfromthoseoftheknownone:thefinestructuresmay(liftereveniftheamino-acidsequenceofthetwoproteinisverysimilartoeachother.
MethodThissectiondescribestilemethodsusedillmyinverse-foldingschenm.
Thefirstsubsectionil-lustratesthetechniqueappliedtothestructurefragnlentclassificationatvariousseale~s.
Thesec-ondsubsectionshalldefinetheprimaryconstraintsbetweenthestructuretypesandthet)rimaryse-quencefragments.
AndthenIformalizesthescor-ingfunctionfortheinversefoldingproblem.
Thelastsubsectionshallillustratethedynamicpro-gramnfingwithA*algorithmappliedtothealign-lnentbetweenthesequenceprofilederivedfromthe3Dstructureandtheanfino-acidsequence.
ClassificationofStructureFragmentsTheclassificationofstructurefragmentsisthenmstcrucialpartofnlyinverse-foldingscheme.
Agoodclassificationmayproducegoodresultswithhighdegreeofaccuracy.
Inordertoincorporatetherelationshipbetweenalargestructureflag-mentandtheprimarysequenceatthatregiomwehavetoclassifynotonlythesmallstructurefragnlcntsbutlargeones.
Howevertheclassifica-tionofthoselargeonesisdifficultwithoutsometechniquetoabstractthestructurebecauselargestructureshavemanydegreesoffreedom.
Iover-camethedifficultybyintroducinglineartransfor-mationofstructurefragmentintofixednunlberofnumericalparameters.
Here,thefixednumberofparanletersareextractedfromthestructurefrag-nlentsofanyscale,andthen,theyareclassifiedintoseveraltypesbysophisticatedclusteringtech-niquesateachscalelevel.
Amongtheparametersrepresentingthestructurefragments,sonlerepre-sentthestructureshape,aaldothersrepresenttheenvironmentaroundthestructure,howthestruc-turefragmentisburiedintheproteinmoleculeorhowexposedtothesolvent.
First.
Ioverviewthetechniqueappliedtothepa-ralneterizationofstnmtureshape.
Thisisdetailedintheliterature(Onizukaetal93).
ThemIanlgoingtoillustratehowtoparameterizctheenviron-nlentaroundthefragments.
ThetechniqueappliedOnizuka315tothestructureclassificationwillbebrieflyillus-trate(l.
Finally,Iwillbeshowingthedescriptionexamplesofproteinstructureusingtheclassifica-tionatmultiplescales.
TopologicalParametersInordertorepresenttilt;shapeofstructurefraglnentswithsmallmun-herofparameters,Iappliedliuem"transfo,wlatio.
ntothecooTdinaterepresentationofastruct.
u.
rcfrog-merit.
Thesetofexpansioncoefficientsobtainedfl'Olnthetransformationturns()tittol)e,afteraslightmodification,tilesetofparametersrepre-sentiugitsabstractedshape.
Wecanrestrictthelmml}eroft}aramctembychoosingacut-offorderintheexpansion.
ThistralmformatimlshallnotloosetheimportantfeatureofthelargestructureI}{~auscthesignificantcoe]~icientsusuallyappearatthelowerordersinthelinearexpansion.
Thecut-off,here,isequivalenttotheneglectoftheuse-lessinfonnationontheshN)eathigheror(lets.
kStructurefragmentwith5residuesOriginPositionalVectorsweightedbytp~.
.
1~484.
.
/:,':~ii',%,J{,SoFigure1:AbstractionofStructureFragmel,tThet)rocedureofthel}aranmtcfizationinvolvessevcrMstepsasfollows.
First.
asetoforthonor-lnMbasesforlinearexi)ansionisi}rovided.
Sec-ond,thesetoftopologicalvectorsiscalculatedastheabstractedformofastructurefraglnentbylin-earlyexpandingthecoordinatercprascntationofthefragment.
Thenwcextrax:ttheorie.
lktationin-variantparametersfrolnthesetoftopologicalt)a-rameters.
Finally,wedefineaparityparameterthatdiscrilninatethemirrorimages.
Thesetofbasesforthelim.
'arexpansioninthisstudynmstbeorthonormalinthediscretesystem.
Aspecialsetisthusrequired.
Oneofthesimplest316ISMB-94setofI)asesisdefimxlbypolynomials.
LetNbethenmnberofCOnlponelltsoftileI}a~se.
LetC2N.
~.
,denotethe.
ithColnponcntofthcbaseofkthor(h.
'r.
Thisissimplydefinc.
dbyakthorderl)olynomialofx.
~ON.
ki=VO~v,k(zi)=e+c~:r,+r2x~+ca:rai+.
.
.
+ckx~.
Theorthonorn,alcon(littonforthissetis.
N-IN.
ji~oY.
~,.
,jI,:i=o(l}N-~):1=(~o~,-.
~,i=0LetSidenotethepositionalvectorrel}re.
sentingthepositionofithresidueinastructurefragment.
ByoperatingtheorthonornmlI}a~eqON.
k,totheseriesofthepositionalvectorsSi.
wecanobtainatopologicalvectorT~astheexpansion(:oeffici{mtsofthelinearexI)ansion.
N-1Tk=~_,~N,kiSi.
(2)i=1}Thesetoftopoh)gicalw~ctorsareth{'abstractedformthefragment.
Col~sideringthepropertiesoftheI)~sesusedto('alculatethesevectors.
T~rel}-resentsai)proxinmtelytheabstra,:tcdlengthofthestructurefraglnent:T2representsapl)roxinlatclytheatxstrax:t{,(Icurvature;T3obviouslyrei)resentsthetwi~t:T4representsthemeaudel'.
ThedirectionofthetOl}ologicalvectorsdependsontheabsoluteorientationofthestructurefrag-meat.
Wehavetoextracttit{;orientationiuvariantl)arame.
tet>.
Inaddition,wenee{1to(lefincapar-ityparametertodiscriminateOllefrontitsmirrorimage.
Hence.
elevenparametersarerequiredtorepresentastructure:fourforthehmgthoftoi}o-h)gicalve('torsITilsixfortheM)solutcdifferencebetweenthetwovectm~IT,-Tjlandonefortheparity.
Theparityl)aramctertakessuchavalueasfollows.
Thesignoftheparityparameterofastructureisdifferentfrontthatofitsmirrorlinage.
Ifthesignisnegativeforastructure,l}ositiw'isthesignforitsmirrorimage.
Thei)ltensityofthepality1}aramcterisslnallwhenthestructureisnearlysymmetric,whilelargeisitwhenstronglyasymmetric.
Wecanobtainsuchat)arameterbycalculatingthevectorproductoftopologieMvectors.
Idefinedtheparityparalne.
terPas({(T1-T2)*(T~T3)}.
Ta-Ta)/L2.
whereLisaconstantspecifictothescaleofstructure,whose.
(limensiouisleugth.
Lisdefinedasthemeanlengthoftopoh}gicalvec-tors.
Hence.
thedimensionofallthetopologicalt)arametm~istheleugth.
EnvironmentalParametersHere,Idiscusshowwecan1incorporatethesolventaccessibilityofstructurefraglnentsintothestnlctureclassifica-tion.
Moreaaldmorebiologistsareawareoftileim-portanceofhydrophobicinteractionbetweentheresidues(luringthefoldingprocess.
Aproteinchainsofoldsintoatertiarystructurethatthehydrophobicresidueswouldbeburiedinsidethcmolecule,whereasthehydrophilliconesexl)osedtothesolvent.
Thehydropathyofeachresiduemustbeastrongfactordetenniningtheenvironmentaroundtheresidue.
Whenastructurefraglnentisdeeplyburiedinthemolecule,mostresiduesillthefragmentshouldbehydrophobic,whilehy-drophillicwhenexposedtothesolvent.
Indeedisitthat,whentilefragmentishalfburiedandhalfex-posed,theresiduesaroundtheburiedregionshouldbehydrophobicandotherresidueshydrophillic.
Thepropensityofeachaminoacidtypetotheell-vironlnentisconsideredevenstrongerthanthattothesecondarystructure(Saitoctal93).
Consid-eringtilepropensityfromtheprimarysequence~wecallestimatehowthcthestructurefl'agmeutwouldbeburiedorexposed.
Illordertochar-acterizetheenvironmentaroundastructurefrag-ment.
Iintroduceanewparanmtcrattachcdtoeachresidueillthestructure,theQuasiBuriedDepth(QBD),whichtakespositivevaluewhentheresidueisburiedinsidethemoleculewhiletakc~negativevaluewhenexposedtothesolvent.
Thedimensionoftheparameterislengthsothatthccalculationwiththetopologicall)arametersphysi-callywouhtmakesense.
First.
IgivethedefinitionofQBD,andthenIillustratehowtoparameterizethesolventaccessibilityofastructurefragment.
Aresiduedeeplyburiedinsidethemoleculeissur-roundedbymoreresiduesthanthoseexposedtothesolvent.
Thenumberofresiduesnearbyagivenresiduewithinacertaindistancecanbeconsideredtomeasurehowtheresidueisburiedorexposed.
Thisnumberisgivenbycountingthenulnberofresiduesillaspherewithcertainradiuscenteredatthepositionofagivenresidue.
Thepredictabil-ityofthisnumberfromagivenprimarysequenceisdiscussedintheliterature(Saitoetal93).
TheQuasiBuriedDepthisderivedfromthenmnl)er.
andhastiledimensionoflength.
FromtheinvestigationoftilelnmxinnunnunlberofresiduesMinaspherewhoseraxliusisr,IfoundthatMisalmostproportionaltother2"45,andiscalculatedasM=0.
15r2"45.
Thissuggests,theresiduesarenotoptimallypackedbutarcsubop-timaUypackedinthesenseoffractaldimension.
WeCallconsiderthatwhentheactualnumberofresiduesNinthespherewithradiusrcenteredatagivenresi(hmw(nfldI)eequaltoM,tiledepthfromthesurfaceoftilel)roteinlnoleculetotileresiduewouldbeestimatedgreaterthanr,whilethedepthwouldbee~stimatedaroundzerowhenNisahalfofM.
ThenulnberNcanbc,therefore,transformedintothequasidel)thoftheresiduefromthesurface.
TheQuasiBuriedDepthdQis,therefore,calcu-latedasdQ=(2N/M-1)'r,whereM=0.
15r2'45.
WhendQtakesapositivevalue,theresidueiscon-sidcredburied,wlfileconsi(teredexposedfortheuegativedQ.
Likewisethetopologicalparameterswhichareol)-taine(lbylineartransformation,thesetofenvi-ronmentalparametersrepresentinghowastruc-turefragmentisburiedorexposediscalculatedI)ytrzmsformingthesetofr~i(lues'QBDillastruc-turcfragment.
TheenvironmentalparameterofkthorderE~iscalculatedasbelow.
N-IEk=~~N.
k~d,(3)i----0wlwrcd~2istheQBDofithresidueillthefrag-meut.
Sincethephysicaldimensionofenvironmen-talparametersislength,theseparametersCallbeusedwithtopologicalparameters.
Illmystudy,thenlaxinmmorderofexpansionisfive,andfiveenvi-roulnentalparametersaretorepresentthesolventaccessibilityofthestructurefragment.
ClassificationofStructureFragmentsThestructurefragmentabstractedandrepresentedwithafewt)arametersmaybeclassifiedI)3,aclus-teringtechniques.
IadoptedLeaningVectorQuan-tization(LVQ).
LVQclassifieseachdataillthedatasetaccordingtothenearestccntroidtothedata.
ThedistancebetweentwodataDisis,inmystudy.
definedtheEuclidiandistaalcebelow.
D~j=i~_,(Ti,~-Tj,k)2,(4)whereTi.
kisthekthcomponentoftheithdata.
ThecentroidsfortheclusteringhereareobtainedI)ytheiterativeprocessasfollows.
Theinitialccn-troi(lsarearbitraryplacedillthen-dimensionalspacewherenisthenuml)erofcolnponentsofthedata.
Eachdatainthesetisclassifiedaccor(lingtothenearestinitialcentroidtothedata.
Bythisinitialclassification,thedatasetisclassifiedintotheclustersrepresentedbyeacheentroidrespec-tively.
Eachcentroi(linthenextstepiscalculatedasthemeaalofthedatabelongingtothecluster.
Thenthedatasetisagainclassifiedaccordingtothenewceutroids.
Tiffsprocessisiterateduntilthedifferelwcbetweenthepopulationofea~llnewclusterandthatofpreviousoneislessthan2%ofOnizuka317thepolmlatiomwhenIconsiderthatthepositiouofeachcentroid~hllostCOllVel'ges.
Scale012312997654933251713975CCCCCCCCCCABBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBCCNNNNNOOCCCCCJJJJJJOCCCCCCCCCCCCCCEJJJQQQ0qQOqQOJJLLLLCCCCCCLLCCCCCCCGFFFCJJOqJJLLLLLRRRRRJJBBBBBBBBBBFFGOOOPPPPPGGGEEHHHJJJJJJLIIKKKKKKUUUAACEELLLLLLLLLFFFBBJJSSSSRKIBHHHIIIPCAGGGKKKKKKKKKKKDDDAIOUUUULHHIIMMLWULMABIIIIOOOOOOIGGGGBBHHTTTTHLFFFHWUUUNEEPKOOOOOOOOOOGGGAEJLQQQQLDAFFWWWVSQJOLEMMMMMMMMMMEEDAJFPPPPPSJDADSSP-eeeee-ssshhhhhhhhhhhhhhhtt---eeeetSeq.
MKIVYWSGTGNTEKMAELIAKGIIESGKDVNTINVScale45612997654933251713975BBBBBBBCBBBBBBBBBCCCCCCCCCCCCCCCCCCCCCCCCBCCCCCCCFFFEEEEEEEEJJJJFFFCCCCCEEECCFFFIIIIIIJJJJFFFEELTTWWWQPJEBBFFFFBUUUWTTTLLLCACIKKKRRRSJJJJJJEEEHHUUUEHHOOOTWWWVKKDDDFFFIMIIIIMMMMMIGEEEMMEGBOOOVSXWWRCCCCBEJJEEEEJJJJJJMMEHFDDEEBNOVVVXXUULAACCHRLABEDDDDDDDDHDCBBBFCMMVWXXXUUSDEECLLNEABBGBBBBBFIHABAAAFOLWWWXXVVSJJDLQNJBBCDDAAABDSSPtt--sttttt-seeeeee--btttb--ttthhhhhSeq.
SDVNIDELLNEDILILGCSAMGDEVLEESEFEPFIScale7890129976549332517[3975BBBBCCJJCEEEEEEEEENNFFFFBBBIIIHONGGGGFFCIIJQqPPPPLLLLLSSSTOUXXTUMMMCCCFFFJRRRRRIIEEEHHHHQOQNNLO000WTTTVKKAAAGGMMMMMMMMFFIIHEGJORRLGIOOSSXXWRRCCCBEEJJJJJJJJJDDEEDILODFFQQNNVVXWWUULACCQEEEGGGGEEGEEBBHTBBFFJFPRWWWWXUUSDEJMGGKGGGBGGBBGICMAADBFFBLTWWWWXVVNKFOOLCEDGCEDGCDDBODSSPhhhstt-tt-eeeeeeeesss-shhhhhhhhhhhhSeq.
EEISTKISGKKVALFGSYGWGDGKWMRDFEERMNGScale12312997654933251713975QLLACEFA(KKRRRRKKKBBBHHHMMMMUUUUUUPHCCDDIGGJJJKKJRMLQQTWRMMMMBFEEEEIIIIIGGUULNMRRWUSNNNAACMKKKKKKKKGGLSSNJOOTWSQQONABBFDGEEGGEEGCADSSPtt-ee-s--eeees--ggghhhhhhhhhhhht-Seq.
YGCVVVETPLIVQNEPDEAEQDCIEFGKKIANI318ISMB-94DescriptionExamplesThedatasetusedinthisstudywastakenfromtheselectedpro-teinstructuresofProteinDataBankbyEMBL(Hobohmetal92).
Fromtheselection.
Ifitrtherselected245structuredeterminedbyX-raychrys-tMlography.
Thesequencehomologyl)etweeneachpairofproteinchainsisalwayslessthan25%.
TheradiusofspheretodeterminetheQBDis11)~.
ThedatasctatN-residuelevelisobtaiuedbycalculatingtilesixteenparametersofallpossibh,'structurefragmentswithNresi(lm~inallthese-lccte(lproteinchains.
Iclassifiedthestructurefragnlelitswith5.
7.
9,13,17,25.
33,49,65,97.
129,aml193residuesandobtaiuedthetwentyfourtypesateachscale.
ThelettersfrolnAtoXdenotethestructuretypes.
Thecouformationof4FXN(Flavodoxin)is(k~cribedinthisschemea.
~above.
Thelinesat"DSSP-denotethesccon(larystruc-turesa.
~signedbyDSSP.
Atthe5-residuelevel,thesitesymboledA.
E,G.
orMusuallytakcshelicalconformationdenotedbyh,andthoseofV.
WorXusuallytakestrandsdenotedbye.
Thestru('-turetypesattim5-residuelevel,therefore,well(:or-r(,'spott(Itosecoudarystructures.
Thedes(~ril)tionathighlevc,lscani)econsi(lcredtorepresentsu-perseronda'tT]struchw(',s,andthoseatthe65or129-residuelevelwouhlcorrespondtothesomedoma'in.
sorgh,balstructm'e~s.
Wecan,'oneludethattheMSSDpreciselyrepresentsthehierar(:hi-calprol)extyof3Dproteinstructure.
Inthisway.
aproteinconformationdescribedinthismulti-s('alestructure(lescriptionschenwshowshowtheconformationisbuiltUl,ofthesubstruc-turesandstructuralmotifs.
PrimaryConstraintsTilt:primarycoustr~iutsrelatetheprimal~se-(luenceandthestructuretypeateax:hregiou.
MSSDschemeist)articularlysuitat)letomodelbothh)ealandglol)alfactorsofstructure,h)rma-tion.
The1)rimaryconstraintsfl)rshortstructurefragnmntsnatundlyrepresentlocalfact()rs,andthoseforhmgon(,'srci)resentglobalorlong-rangefactors.
Forhlrtherdiscussion,Idefineseveraluo-tationshere.
Let7~(lenoteastructuretype,whereimrinally71k=Ak,7~"=Bk.
.
.
.
.
~ff6=pk.
Letc~k,lenot,,aprimarysequencefragmentattilekthlevel.
An(1wefllrtherdenote.
wka~thenumberofresiduesinthestructurefi'agmentattilekthlevel.
WedenoteF~"E{AI',Bk.
.
.
.
.
X~}asthevariablethattakesastru(:turetype.
wherei(leuotesthepositionthel)rimarysequence.
WealsodenoteE~astilt,,variablethattakesaprimarysequencefragntent.
Notethatthepositiollihcredenotesthepositionofthefirstrt,'shlucoftilestructurefragmentinthe,prilnarysequence.
Theprol)M)ilityofaprimarysequencefraglnentakformingatypeofstructure%~"isrepresentedaspp(r~_k,~k=ak="ltli).
SinceweassumethattheprimaryconstraintisinvariantofitsM)solutepositionilltileprimarysequencebutonlydependsoutilestructuretypeandtileprimawse(luenceatthatregion,itlnaysilnplyt)erepresenteda.
spp(r~lzk).
Inthepreviousliteratures(Onizukaetal93:Onizukaetal94).
Idefinedgeometriccon-straintsbetweentheoverlappingstructurefrag-ments,whichisessentialfactorfor3Dproteinstructurepredictionabinitio.
Inthispaper,Idon'tdiscussonthisissuebecausetheyhavenothingtodowiththeinverse-foldingschc,ncusingMSSD.
InthefieldofmolecularbiologT,thesequencepro-filesarefrequentlyusedtoanalyzetherelation-shipbetweenasequencepatternandthestructureorfunctionatthatregion,wherethefrequencyofeachamino-acidtypeiscountedwithr(~l)ccttotheposition.
Thistechlfiqueisdirectlyappli-cabletomodeltheprinlaryconstraintsatsmallscales,thoughitrequireslargelmmberofparam-eters,again,fortheprimaryconstraintsatlargescale.
Forcxamplc,atfive-residuelcvel,thenum-berofparalnetersrcpresentingthefrequencyis100=20x5where20isthenumberofaluilm-acidtype~,and5istilenulnl)erofresiduesilltilestructurefragmentatthatlevel.
Atthelargescalelevels,wherethenumberofresi(luesaremorethan100,nmrethan2000parametersarerequired.
Inthiscase.
however,wecancomt)resstheseqummcprofileusingthesametechlfiqueasIappliedtothestrm:tureal)straetion.
Wecanalwaysreducetilexmnlberofparametersinto100usinglinearCXl)aal-sionagain.
Inverse-foldingSchemeGivenanMSSDret)rescntinga3Dl)roteinstruc-turc.
wecanestinlatcthemostprobablesequencefi'omtheMSSDusingtheinverseprimarycon-straintsPI(EIF),whichissimplygivenbycalcu-latingtilefitofase(luencetoaprofile.
Pp(FIE)iscalculatedbyai)i)lyingthepriorP(F)toPI(EIF).
Letidenoteapositioninthesequence.
LettAdenoteallamino-acidtype.
~ndletTAbeavari-al)lethattake~oneoftheaminoacidtypetA.
WeCallderivetheprobabilityP(TA=tA)oftheanfino-aeidtypeoecun-iugatthepositioni,fromtilestnmturefragmenttypecoveringthepositionAAi.
LetPI(Ti=t]['j)denotetheprobM)ilitythealnino-acidtypetAoccurringatthepositio,tiinthefragment.
TosuperposethePI(TA),wehavetodividethisvaluebythepriorP(TA=tA),becausetilepriorisdoublyortriplycalculated.
Thus,PI(TA)iscalculatedasbelow.
p(TA----tA)=p(tA)PI(TA=talrJ)P(tA)AllP1~overinffi(5)Inthisease,however,thepriorP(tA)doessome-tiringunpreferable.
TheprobabilityP(Tff=tA)almostalwayssuggeststhatAlanineistilemostprobableamino-acidtypeatallyposition.
Thislneemsthattheinversel)rilnatTconstraintPI(TAIEj)ismuchweakerthantheprior.
Hence,IadoptC~(Tff=tA)=Pt(Tff=tA)/p(tA)in-steadofPx(TA=ta).
Thisvalueisgreaterthan1.
0whentheamino-acidtypestochasticallyoccursmorethanrandomlevel.
Thesuperpositionof'alltheinverseprimal5,con-straintsfromtheMSSDderivedfi'onlthegiven3Dstructureyieldsastocha,stiesequenceprofile.
Thefitofasequen('etothisprofileisconsideredthefittothegivenconformationrel)resentedbytheMSSDandl)yturnthefittothegiven3Dstruc-ture.
3D-1DAlignmentThealiglunentbetweenthese(luenceandthepro-fileiscarriedoutsimplybydynamicprograulnfing.
Thedynamicprograumlingsearchesfortheopti-ur,flalignmentthatminimizethescoreEbelow.
Someal)t)rol)riategappenaltyshouldbeusedwheuwel)ernfitgaps.
=-ElogCI(TiA=tA)+9appen.
alty.
(6)EiWeconsidertheresultantscoreEasthefitofamino-acidsequeucetothcsequenceprofileCI(TA)derivedfromtheMSSDrepresenting3Dstructure.
Hence,giveuaprimarysequenceofaproteinwhose3Dstructureisunknown,wecansearchforthcmostcompatible3Dstructureintheproteiustructuredatabase.
ThisisfarsimplerthanthatofthoseschenlesusingSipplpotential(SipplandWeitckus92:Jonesetal92;YukcamlDill92;SkolnickandKolinski92),whereitisnecessarytoapplythedoubledynamicprogralnnfingthatre-quireslargeamountofcalculation.
IappliedtheA*algorithmtotile3D-1Dalign-meut,whichwasfirstappliedtotheproteinse-quencealignmentintheliterature(Arakietal93).
Thisalgorithmfindstheoptimalsolutionwhilethecalculationamountisnmchsnlallerthealthatofeonveutiona,1dynanficprograanmingalgorithms,thoughtheinlplcmentatiouismuchdifficult.
Thechoiceofthegappenaltyhasnotyetestab-lished,himostcases,therearethreeparame-tcmconcenfingthegappenalty:1)theslidegapOniznka319penaltyisthe(:()stforthcoffsetI)etweenthesequence;2)tileinitialgappenaltyisthecosttoputagapinasequence:and3)theincrementalgappenaltyisthecostfortheh;ngthofeachgap.
Whcntheinitialgappenaltyequalstoincrcnmll-telone,the(lynanficprogramnfingturusouttobequitesimplewithasimplenetwork.
Thus,Iadoptedthispcnalty.
Theslidepenaltyshouhlbezerotoallowanyoffsetbetweenthesequenceandprofilewithoutcosts.
ResultsIusedthesamedatasetoft)roteinstructuresa.
sthatusedforstructureclassification.
Tocross-validatethe,result,thedatasetwasdividedintofivegroupsrandomlysothateachgroupwouhlcon-tainfortyninestnlcturcdata.
Iobtainedfivesetsofp1~maryconstraints,whereeachsetwasderivedfromthestructuredatainfivegroups.
Whenastructureyieldsthesequenceprofile.
Ididnotusethoseprimaryconstraintsthatarederivedfl'omthestructuregroupincludingthatstructurc,.
First,asal)reliminaryexperiment.
Iinvestigatedhowaproteinsequencefitsitsown3DstructureevaluatingtheZscore.
Here.
Ididnotaligntheprofileaadthesequence:thegapsarc.
thus.
notconsidcre(I.
WecanobtaintheZscoreofase-quencctoaprofilebynormalizingthescoreEbythemeanscoreall(Ithe(levia-tionCrEr,,,a.
.
.
.
ofraa~(lonlS(Xluen(:estothatprofile.
whereEisdefineda.
sbelow.
-ElogC1(7~A=tA).
(7)EiThus.
ZscoreEzis,E-(ErandomEz=(8)CIEr,,.
doraIinvestigatedthefitofse(luencestothestnlcturesatonlyOllescalelevel,inordertoseewhichh;velbestcorrespondsthesequence.
TheplotbelowshowstheineanZscorewithrespecttothescalelevel.
Thecorrespondenceisthebestatthelow-est5-residuelevelandit(lecrca;seslnonotonouslywiththeincreaseintilt;level.
Thissuggeststhatalocalsequencestronglyinfluencethefonnationofthesecondarystructuresatthatregion,becausetheclassificationatthe5-residuelcw;lwellcorre-si)ondsthesecondarystructures.
Probablyduetotheover-learning,thescoresatthehighlevelsarebelowzero.
Second.
IcheckedwhetheraseqUellCewouhliden-tifyitsownstructurc.
Thchit-ratiooftheself-identificationdirc('itysuggeststhet)erfonnan('cmyinversc-fi)ldingschemc.
Icl.
eckcdwhetherthefitofasequencetoitsownstructurewouklscorcs320ISMB-94\\i.
.
.
.
.
.
:oScale(NumberofResiduesin"Fragments)Figure2:ZScorevel~usScalethc,bestamongallsequence-profih:combillations.
Wcselectcd188proteinstructuresfromthedatasetwhichIusedtomodeltheprimaryconstraints,becausetheotherstructuredatacontainresi(hm-lacksorunacceptablebondlengths.
Iinw'st.
igatedthehit-ratioofself-identification.
Whenthe('onl-patil)ilityscoreofthesequencetoitsownstruc-tureobtainedfromthe3D-1Dalignments('orcsthebest.
Iconsiderthattheidentificationhits.
Ididexhausting3D-1Daligammntfor188*188times.
Thetal)lcbelowshowsthehitratiom~s.
ITotal[Hit]HitRatioISingleLevel188630.
335[Multi-Leveli88900.
478IThisresultactuallyshowsthatthepel'formanceofself-identificationisbetterwhenmanyscalelevelsareincorporated.
HitRatioiii.
.
:.
4.
GapPenaltyFigure3:HitRatioversusGapPevaltyThirdIinvestigatedhowthegapl)enaltyinflucn(:ethehitratio.
Inthiscase,Iusedonlyfirstgroupofdatasetwhichcontainsthirtynineproteins.
Thisgraphshowsthattilehighertilegappenaltyis.
tilebctteristhehitratio.
DiscussionInthispaper,Iproposedthenndti-scaleevaluationschemetosolvetheinverseproteinfoldingprob-lem.
Iincorporatedtheconq)atibilityofsequencesto3Dstructuresnotonlyatthesmallscalelevelbutalsoatthelargeseal(;levels.
Theresultsshowthatthemulti-scalecompatibilityscoringworksbetterthanthesinglescale()ale,eventhoughthecompatibilityscoresatlargescalelevelspoorlycorrespondsthefitbetweenthestructuresandsequcncesbetterthanthoseatsnlallscalelev-els.
Consideringsizcofdatasetcontaining188proteinstructures,theresultisnotsobad.
Oneofthedifficultproblemsunsolvedishowwecaaldetel'minethegapl)enalty.
AsIshowedthehitratioversusgappenalty,thehigherthegappenaltyistilebetteristhehitratio.
Iuthissense,forthebetterperformance,thegappenaltyshoudbehigh.
However.
thehighgappenaltydoesnotper-mittherobustidentification.
WhycanweinsertgapsinthealignmentsThegapsinastructureInaychangethestructure,andthen,thedifferentenvironmentmaybeformed.
ThelengthofexteriorloopsofaI)roteinstructureisvariable.
Eventhemainchaintopologylooksalike.
Wehavetopermitthegapsintim3D-1Dalignment.
However,therobustidentificationbyturnproducesworseself-identificationhit-ratio.
ConsideringthepoormeanZscoreathighlev-els,the3D-1Dcorrespondenceathighlevelsdoesnotseemtobestochasticallylnodelabie.
Thus.
wcshouldnotusethoselevelsinordertoobtainbetterself-identificationhit-ratio.
IinvestigatedtheapplicabilityofMSSDschemetotheinversefoldingproblem,andfoundthatthenlulti-scMescoringworksfarbetterthansin-glescalescoring.
Thismeansthatthescoreathighlevelsdoesagreatdealtoenhancetheperfor-nlance.
ReferencesOnizuka.
K.
;K.
Asai;M.
Ishikawa;andS.
T.
C.
Wong1993.
"'AMulti-LevelDescrit)tionSchemeofProteinConformatioll".
P'roc.
ofISMB-93:301-310.
CyrusChotlfia1992.
"Onethousa~Mfamiliesforthemolecularbiologist".
Nature357:543-544.
Bowie.
J.
U.
R.
Liithy,andD.
Eisenberg1991.
"AMethodtoIdentifyProteinSequenceThatFoldintoaKnownThree-DilnensionMStructure"SCI-ENCE253:164-170.
Sil)pl,M.
,andS.
Weitckus1992.
"DetectionofNative-likeModelsforAminoAcidSequcnees".
PROTEINS13:258-271.
Goldstein,R.
A.
,Z.
A.
Luthey-Sclmltcn,andP.
G.
Wolynes1994.
"ABayesianApproachtoSe-quenceAlignmentAlgorithmforProteinStruc-tureRecognition".
Proc.
of27thHICSS5:306-315.
Onizuka.
K.
.
K.
Asai.
H.
Tsuda,K.
Ito.
M.
Ishikawa.
andA.
Aiba1994.
"'ProteinStructurePredictionBasedonMlflti-LevelDescrit)tion".
P~vc.
of27thHICSS5:355-354.
Saito.
S.
.
T.
Nakai,andK.
Nishikawa1993.
"'AGeonleticalConstraintApproachforRcl)roducingtheNativeBackboneConformationofaProtein".
PROTEINS15:191-204.
Hobohm,U.
,M.
Scharf,R.
Schncider.
C.
Sandcr1992.
"Selectionofarepresentativesetofstruc-turesfromtheBrookhavenProteinDataBank".
ProteinScience1:409-417.
Jones,D.
,W.
Taylor,andJ.
Thornton1992.
"'ANewApproachtoProteinFoldRecognition".
Na-ture358:86-89.
Ynke,K.
,andK.
Dill1992.
"InverseProteinFold-ingProbleln".
Pivc.
Natl.
Acad.
Sci.
USA89:4163-4167.
Skolnick,J.
.
andA.
Kolinski1992.
"'TopologyFin-gcrprintApproach".
Science250:1121-1125.
Araki,S.
,M.
Goshinla.
S.
Mori,H.
Nakashima,S.
Tomita,Y.
Akiyama.
andM.
Kanehisa1993.
"'Ap-plicationofParailelizedDPandA*AlgorithmtoMlfltit)leSequenceAlignment".
Proc.
ofGemomeInformaticsWorkshopV:94-102.
Onizuka321
- transfowww.hhh258相关文档
- offspringwww.hhh258
- domainswww.hhh258
- DPMwww.hhh258
- 旭日www.hhh258
- Limitedwww.hhh258
- Q1www.hhh258
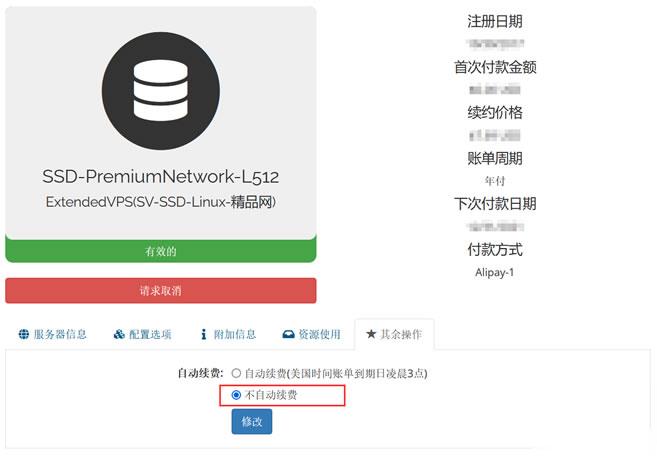
Raksmart VPS主机如何设置取消自动续费
今天有看到Raksmart账户中有一台VPS主机即将到期,这台机器之前是用来测试评测使用的。这里有不打算续费,这不面对万一导致被自动续费忘记,所以我还是取消自动续费设置。如果我们也有类似的问题,这里就演示截图设置Raksmart取消自动续费。这里我们可以看到上图,在对应VPS主机的【其余操作】中可以看到默认已经是不自动续费,所以我们也不要担心被自动续费的。当然,如果有被自动续费,我们确实不想续费的...
Vultr VPS新增第18个数据中心 瑞典斯德哥尔摩欧洲VPS主机机房
前几天还在和做外贸业务的网友聊着有哪些欧洲机房的云服务器、VPS商家值得选择的。其中介绍他选择的还是我们熟悉的Vultr VPS服务商,拥有比较多达到17个数据中心,这不今天在登录VULTR商家的时候看到消息又新增一个新的机房。这算是第18个数据中心,也是欧洲VPS主机,地区是瑞典斯德哥尔摩。如果我们有需要欧洲机房的朋友现在就可以看到开通的机房中有可以选择瑞典机房。目前欧洲已经有五个机房可以选择,...

HostKvm - 夏季云服务器七折优惠 香港和韩国机房月付5.95美元起
HostKvm,我们很多人都算是比较熟悉的国人服务商,旗下也有多个品牌,差异化多占位策略营销的,商家是一个创建于2013年的品牌,有提供中国香港、美国、日本、新加坡区域虚拟化服务器业务,所有业务均对中国大陆地区线路优化,已经如果做海外线路的话,竞争力不够。今天有看到HostKvm夏季优惠发布,主要针对香港国际和韩国VPS提供7折优惠,折后最低月付5.95美元,其他机房VPS依然是全场8折。第一、夏...

www.hhh258为你推荐
-
22zizi.comwww 地址 didi22怎么打不开了,还有好看的吗>com5xoy.comhttp://www.5yau.com (舞与伦比),以前是这个地址,后来更新了,很长时间没玩了,谁知道现在的地址? 谢谢,se95se.com现在400se就是进不去呢?进WWW怎么400se总cOM打开一半,?求解sesehu.com68lolita com是真的吗www.idanmu.com腾讯有qqsk.zik.mu这个网站吗?www.175qq.com这表情是什么?www.147.qqq.comWWW147EEE.COM这个网站现在改哪个网址了hao.rising.cn如何解除瑞星主页锁定(hao.rising.cn). 不想用瑞星安全助手猴山条约猴的谚语有哪些chudian365正泰电器 触电たNBE7LE 2P63A 二极漏电断路器C63怎么样