Figopeneuler
openeuler 时间:2021-03-17 阅读:()
AInnitesetsThisappendixgivesaminimum-fusssummaryoftheset-theoreticno-tionsandfacts,suchasZorn'slemmaandtransniteinduction,thatareusedinChapter8.
LetA,Bbesets.
IfthereexistsabijectivemapbetweenAandB,wewrite|A|=|B|andsaythatAandBhavethesamecardinality.
Thisisclearlyanequivalencerelationbetweensets,andwemaythinkofthecardinality|A|ofAastheequivalenceclasscontainingA.
Wewritecardinality|A||B|ifthereexistsaninjectivemapA→B.
Thisisclearlywelldened,anditisapartialordering:ifthereareinjectivemapsA→BandB→A,thereisalsoabijectionA→B.
1Foreverysetthereexistsanotherthatisbigger;forexample,|A||G|,becauseα→xαwouldbeaninjectivemapfromαtoV(G)showingthat|α||G|.
Sincethereexistordinalslargerthan|G|,suchasanyordinalequivalenttoawell-orderingofthepowersetofV(G),396AppendixAthismeansthatourrecursioncannotgoonindenitely,i.
e.
weshallnotbeabletodenexαforallordinalsα.
Wemaynotknowinadvancewhenourrecursionwillgetstuck,i.
e.
,whichisthesmallestordinalαforwhichxαcannotbefoundincompliancewithourrules.
Butthisdoesnotmatter:wesimplydeneαastherstordinalαforwhichxαcannotbefound,contentourselveswithhavingdenedxαforallαp,whicharecompatibleinthatfqpfrq=frpwheneverr>q>p.
GeneralizedInnityLemma.
Foreverysuchfamily{Xp|p∈P}ofnitesetsthereexistsafamily{xp|p∈P}ofrepresentativesxp∈Xpsuchthatfqp(xq)=xpwheneverq>p.
Theinnitylemmaisclearlyaspecialcaseofthis,withP=Nandthefqpdenedbyiteratingthelemma'spredecessorfunctionf.
2Incategorytheory,our'generalizedinnitylemma'isknownasthefactthattheinverselimitofanydirectedinversesystemofnitesetsisnon-empty.
Insteadofnitesetsonecantakeanyothercompactspaces;seeChapter8.
8foranapplication.
Innitesets397Thefollowingmorecombinatorialencodingforcompactnessargu-mentsbringsoutparticularlywellthechoicesinvolved,andtheirinter-dependence.
LetXbeanyset,Saniteset,andFasetofnitesubsetsofX.
AssumethateveryY∈FcomeswithaxedsetA(Y)ofY→Sfunctions,itsadmissiblefunctions.
CallYFcompatibleifthereexistsafunctionf:X→SallwhoserestrictionstothesetsinYareadmissible,i.
e.
whichsatisesf|Y∈A(Y)forallY∈Y.
CompactnessPrinciple.
FiscompatibleifeveryniteYFiscompatible.
TheproofsofthegeneralizedinnitylemmaandofthecompactnessprincipleareeachjustafewlinesbasedonTychono'stheoremthateveryproductofcompactspacesiscompact.
Weillustratethisforthecompactnessprinciple.
ThinkofthesetofallX→Sfunctionsasaproductof|X|copiesofS,sotheyformacompactspace.
ForeveryniteYX,thesetofallfunctionsf:X→Swithf|Y∈A(Y)isclosed(aswellasopen)inthisproductspace.
Theresultnowfollowsfromthe'niteintersectionproperty'ofcompactspaces,thatafamilyofclosedsetshasanon-emptyintersectionassoonasallitsnitesubfamiliesdo.
BSurfacesThisappendixoersasummaryofbackgroundinformationaboutsur-faces,asneededforanunderstandingoftheirroleintheproofofthegraphminortheoremortheproofofthe'generalKuratowskitheorem'forarbitrarysurfacesgiveninChapter12.
7.
Inordertobereadatarigorouslevelitrequiresfamiliaritywithsomebasicdenitionsofgeneraltopology(suchasoftheproductandtheidenticationtopology),butnomore.
Asurface,forthepurposeofthisbook,isacompactconnected1surfaceHausdortopologicalspaceSinwhicheverypointhasaneighbourhoodhomeomorphictotheEuclideanplaneR2.
Anarc,acircle,andadiscarcinSaresubsetsthatarehomeomorphicinthesubspacetopologytothecircleS1realinterval[0,1],totheunitcircleS1={x∈R2:x=1},andtodisctheunitdisc{x∈R2:x1}or{x∈R2:x<1},respectively.
ThecomponentsofasubsetXofSaretheequivalenceclassesofcomponentpointsinXwheretwopointsareequivalentiftheycanbejoinedbyanarcinX.
ThesurfaceSitself,beingconnected,hasonlyonecomponent.
ThefrontierofXisthesetofallpointsyinSsuchthateveryfrontierneighbourhoodofymeetsbothXandSX.
ThefrontierFofXseparatesSXfromX:sinceX∪Fisclosed,everyarcfromSXtoXhasarstpointinX∪F,whichmustlieinF.
AcomponentofthefrontierofXthatisacircleinSisaboundarycircleofX.
AboundaryboundarycirclecircleofadiscinSissaidtoboundthatdisc.
Thereisafundamentaltheoremaboutsurfaces,theirclassication.
Thissaysthat,uptohomeomorphism,everysurfacecanbeobtainedfromthesphereS2={x∈R3:x=1}by'addingnitelymanysphereS2handlesornitelymanycrosscaps',andthatsurfacesobtainedbyaddingdierentnumbersofhandlesorcrosscapsaredistinct.
Weshallnotneedtheclassicationtheorem,buttoformapictureletusseewhatthe1Throughoutthisappendix,'connected'means'arc-connected'.
R.
Diestel,GraphTheory,GraduateTextsinMathematics173,DOI10.
1007/978-3-662-53622-3ReinhardDiestel2017399400AppendixBaboveoperationsmean.
ToaddahandletoasurfaceS,weremovetwohandleopendiscswhoseclosuresinSaredisjoint,andidentify2theirboundarycircleswiththecirclesS1*{0}andS1*{1}ofacopyofS1*[0,1]disjointfromS.
Toaddacrosscap,weremoveoneopendisc,andthencrosscapidentifyoppositepointsonitsboundarycircleinpairs.
Inordertoseethattheseoperationsdoindeedgivenewsurfaces,wehavetocheckthateveryidenticationpointendsupwithaneigh-bourhoodhomeomorphictoR2.
Todothisrigorously,letusrstlookatcirclesmoregenerally.
AcylinderistheproductspaceS1*[0,1],oranyspacehomeomor-cylinderphictoit.
ItsmiddlecircleisthecircleS1*{12}.
AM¨obiusstripisanyspacehomeomorphictotheproductspace[0,1]*[0,1]afteridenti-M¨obiusstripcationof(1,y)with(0,1y)forally∈[0,1].
Itsmiddlecircleistheset{(x,12)|0Itcanbeshown3thateverycircleCinasurfaceSisthemiddlecircleofasuitablecylinderorM¨obiusstripstripneigh-bourhoodNinS,whichcanbechosensmallenoughtoavoidanygivencompactsubsetofSC.
Ifthisstripneighbourhoodisacylinder,thenNChastwocomponentsandwecallCtwo-sided;ifitisaM¨obiusstrip,thentwo-sidedNChasonlyonecomponentandwecallCone-sided.
one-sidedUsingsmallneighbourhoodsinsideastripneighbourhoodofthe(two-sided)boundarycircleofthediscordiscsweremovedfromSinordertoattachacrosscaporhandle,onecanshoweasilythatbothoperationsdoproducenewsurfaces.
SinceSisconnected,SCcannothavemorecomponentsthanNC.
IfSChastwocomponents,wecallCaseparatingcircleinS;separatingcircleifithasonlyone,thenCisnon-separating.
Whileone-sidedcirclesareobviouslynon-separating,two-sidedcirclescanbeeitherseparatingornon-separating.
Forexample,themiddlecircleofacylinderaddedtoSasa'handle'isatwo-sidednon-separatingcircleinthenewsurfaceobtained.
WhenSisobtainedfromSbyaddingacrosscapinplaceofadiscD,theneveryarcinSthatrunshalf-wayroundtheboundarycircleofDbecomesaone-sidedcircleinS.
Theclassicationtheoremthushasthefollowingcorollary:LemmaB.
1.
Everysurfaceotherthanthespherecontainsanon-separatingcircle.
2Thisismadeprecisebytheidenticationtopology,whoseformaldenitioncanbefoundinanytopologybook.
SinceS1hastwopossibleorientations,twocopiesofS1canbeidentiedintwoessentiallydierentways.
Thecorrespondingtwowaysofaddingahandleyielddierentnewsurfaces.
Fortheclassicationoneonlyusesoneofthese,thewaythatpreservestheorientabilityofthesurface(asinFigureB.
1).
3Inprinciple,thestripneighbourhoodNisconstructedasintheproofofLemma4.
2.
2,usingthecompactnessofC.
Howeversincewearenotinapiecewiselinearsettingnow,theconstructionisconsiderablymorecomplicated.
Surfaces401Weshallseebelowthat,inasense,ourtwoexamplesofnon-separatingcirclesareallthereare:cuttingasurfacealonganynon-separatingcircle(andpatchinguptheholes)willalwaysproduceasurfacewithfewerhandlesorcrosscaps.
AnembeddingG→SofagraphGinSisamapσthatmapstheembeddingverticesofGtodistinctpointsinSanditsedgesxytoσ(x)–σ(y)arcsσ:G→SinS,sothatnoinnerpointofsuchanarcistheimageofavertexorliesonanotherarc.
Wethenwriteσ(G)fortheunionofallthosepointsandarcsinS.
AfaceofGinSisacomponentofSσ(G),andthefacesubgraphofGthatσmapstothefrontierofthisfaceisitsboundary.
boundaryNotethatwhilefacesinthespherearealwaysdiscs(ifGisconnected),ingeneraltheyneednotbe.
Onecanprovethatineverysurfaceonecanembedasuitablegraphsothateveryfacebecomesadisc.
ThefollowinggeneralversionofEuler'stheorem4.
2.
9thereforeappliestoallsurfaces:TheoremB.
2.
ForeverysurfaceSthereexistsanintegerχ(S)suchthatwheneveragraphGwithnverticesandmedgesisembeddedinSsothattherearefacesandeveryfaceisadisc,wehavenm+=χ(S).
ThisinvariantχofSisitsEulercharacteristic.
Forcomputationalsimplicityweusuallyworkinsteadwiththederivedinvariantε(S):=2χ(S),ε(S)theEulergenusofS,becauseχisnegativeformostsurfacesbutεtakesEulergenusitsvaluesinN(seebelow).
PerhapsthemoststrikingfeatureofEuler'stheoremisthatitworkswithalmostanygraphembeddedinS.
ThismakesiteasytoseehowtheEulergenusisaectedbytheadditionofahandleorcrosscap.
Indeed,letDandDbetwoopendiscsinSthatwewishtoremoveinordertoattachahandlethere.
LetGbeanygraphembeddedinSsothateveryfaceisadisc.
Ifnecessary,shiftGonSsothatDandDeachlieinsideaface,fandf,say.
AddcyclesCandContheboundarycirclesofDandD,andjointhembyanedgetotheoldboundariesoffandf,respectively.
Theneveryfaceoftheresultinggraphisagainadisc,andDandDareamongthese.
NowremoveDandD,andaddahandlewithanadditionalC–Cedgerunningalongit.
Thisoperationmakesthenewhandleintoonenewface,whichisadisc.
Itthusreducesthetotalnumberoffacesby1(sincewelostDandDbutgainedthenewfaceonthehandle)andincreasesthenumberofedgesby1,butleavesthenumberofverticesunchanged.
Asaresult,εgrowsby2.
402AppendixBSimilarly,replacingadiscDboundedbyacycleCGwithacrosscapdecreasesthenumberoffacesby1(sinceweloseD),butleavesnmunchangedifwearrangethecycleCinsuchawaythatverticesgetidentiedwithverticeswhenweidentifyoppositepoints.
Wehavethusshownthefollowing:LemmaB.
3.
(i)AddingahandletoasurfaceraisesitsEulergenusby2.
(ii)AddingacrosscaptoasurfaceraisesitsEulergenusby1.
SincethespherehasEulergenus0(Theorem4.
2.
9),theclassica-tiontheoremandLemmaB.
3tellusthatεhasallitsvaluesinN.
Wemaythustrytoprovetheoremsaboutsurfacesbyinductiononε.
Fortheinductionstep,wecouldsimplyundotheadditionofahandleorcrosscapdescribedearlier,cuttingalongthenewnon-separatingcircleitproduced(whichrunsaroundthenewhandleor'half-way'aroundthecrosscap)andrestoringtheoldsurfacebyputtingbackthediscordiscsweremoved.
Aproblemwiththisisthatwedonotnormallyknowwhereonoursurfacethiscirclelies,saywithrespecttoagivengraphembeddedinit.
However,thegenus-reducingcut-and-pasteoperationcanbecarriedoutwithanynon-separatingcircle:wedonothavetouseonethatweknowcamefromanewhandleorcrosscap.
Thisisanexampleofamoregeneraltechniqueknownassurgery,andworksasfollows.
LetCbeanon-separatingcircleinasurfaceS=S2.
TocutSalongC,weformanewspaceSfromSbyreplacingeverypointx∈Ccuttingwithtwopointsx,xanddeningthetopologyonthemodiedsetasfollows.
4LetNbeanystripneighbourhoodofCinS,andputX:={x|x∈C}andX:={x|x∈C}.
IfNisacylinder,thenNChastwocomponentsNandN,andwechoosetheneighbourhoodsofthenewpointsxandxinSsothatXandXbecomeboundarycirclesofNandNinS,respectively,andN∪XandN∪XbecomedisjointcylindersinS.
IfNisaM¨obiusstrip,wechoosetheseneighbourhoodssothatXandXeachformanarcinSandX∪XisaboundarycircleofNCinS,with(NC)∪X∪XformingonecylinderinS.
Finally,weturnSintoasurfacebycappingitsholes:cappingforeachofthe(twoorone)boundarycirclesXandXorX∪XofSCinSwetakeadiscdisjointfromSandidentifyitsboundarycirclewithX,XorX∪X,respectively,sothatthespaceobtainedisagainasurface.
4Thedescriptionthatfollowsmaysoundcomplicated,butitisnot:workinginourconcretemodelsofthecylinderandtheM¨obiusstripitiseasytowritedownexplicitneighbourhoodbasesthatdeneatopologywiththepropertiesstated.
Asallwewantistoobtainsomesurfaceofsmallergenus,wedonotcareaboutuniqueness(whichwillfollowanyhowfromLemmaB.
4andtheclassication).
Surfaces403ComputinghowtheseoperationsaecttheEulergenusofSisagaineasy,assumingwecanembedagraphinSsothateveryfaceisadiscandCistheimageofacycle.
(Thiscanalwaysbedone,butitisnoteasytoprove.
5)Indeed,bydoublingCweleftnmunchanged,becauseacyclehasthesamenumberofverticesasedges.
Soallwechangedwas,whichincreasedby2intherstcaseandby1inthesecond.
LemmaB.
4.
LetCbeanynon-separatingcircleinasurfaceS,andletSbeobtainedfromSbycuttingalongCandcappingtheholeorholes.
(i)IfCisone-sidedinS,thenε(S)=ε(S)1.
(ii)IfCistwo-sidedinS,thenε(S)=ε(S)2.
LemmaB.
4givesusalargesupplyofcirclestocutalonginaninductionontheEulergenus.
Still,itissometimesmoreconvenienttocutalongaseparatingcircle,andmanyofthesecanbeusedtoo:LemmaB.
5.
LetCbeaseparatingcircleinasurfaceS,andletSandSbethetwosurfacesobtainedfromSbycuttingalongCandcappingtheholes.
Thenε(S)=ε(S)+ε(S).
Inparticular,ifCdoesnotboundadiscinS,bothSandShavesmallerEulergenusthanS.
Proof.
Asbefore,embedagraphGinSsothateveryfaceisadiscandCistheimageofacycleinG,andletG→SandG→Sbethetwographsobtainedinthesurgery.
Thus,GandGbothcontainacopyofthecycleonC,whichweassumetohavekverticesandedges.
Then,withtheobviousnotation,wehaveε(S)+ε(S)=(2n+m)+(2n+m)=4(n+k)+(m+k)(+2)=2n+m=ε(S).
NowifS(say)isasphere,thenS∩SwasadiscinSboundedbyC.
Hence,ifCdoesnotboundadiscinSthenε(S)andε(S)arebothnon-zero,givingthesecondstatementofthelemma.
WenowapplythesetechniquestoprovealemmaforourdirectproofinChapter12ofthe'Kuratowskitheoremforarbitrarysurfaces',Corollary12.
7.
3.
5PerhapsthesimplestproofwasgivenbyC.
Thomassen,TheJordan-Schoeniestheoremandtheclassicationofsurfaces,Amer.
Math.
Monthly99(1992),116–130.
404AppendixBLemmaB.
6.
LetSbeasurface,andletCbeanitesetofdisjoint[12.
7.
4]circlesinS.
AssumethatSChasacomponentD0whoseclosureinSmeetseverycircleinC,andthatnocircleinCboundsadiscinSthatisdisjointfromD0.
Thenε(S)|C|.
Proof.
WebeginwiththeobservationthattheclosureofD0notonlymeetsbutevencontainseverycircleC∈C.
ThisisbecauseChasastripneighbourhoodNdisjointfromalltheothercirclesinC(sincetheirunioniscompact),andeachofthe(oneortwo)componentsofNChasallofCinitsclosure.
SinceD0meets,andhencecontains,atleastonecomponentofNC,itsclosurecontainsC.
LetuspartitionCasC=C1∪C12∪C22,wherethecirclesinC1areC1,C12,C22one-sided,thoseinC12aretwo-sidedbutnon-separating,andthoseinC22areseparating.
Weshall,inturn,cutalongallthecirclesinC1,some|C22|non-separatingcirclesnotinC,andatleasthalfthecirclesinC12.
ThiswillgiveusasequenceS0,Snofsurfaces,whereS0=S,andSi+1S0,SnisobtainedfromSibycuttingalongacircleCiandcappingthehole(s).
CiOurtaskwillbetoensurethatCiisnon-separatinginSiforeveryi=0,n1.
ThenLemmaB.
4willimplythatε(Si+1)ε(Si)1foralliandε(Si+1)ε(Si)2wheneverCi∈C12,givingε(S)ε(Sn)+|C1|+|C22|+2|C12|/2|C|asdesired.
C9C1C2D0C3C4C5C6C7C8C9Fig.
B.
1.
Cuttingthe1-sidedcircleC1andthe2-sidedcirclesC2,C3andC5,C7,C8andC9doesnotseparateSCuttingalongthecirclesinC1(andcappingtheholes)isstraightfor-ward:sincethesecirclesareone-sided,theyarealwaysnon-separating.
Next,weconsiderthecirclesinC22,suchasC9inFigureB.
1.
ForeveryC∈C22,denotebyD(C)thecomponentofSCthatdoesnotcontainD0.
SinceeverycircleinCliesintheclosureofD0butnoSurfaces405pointofD(C)does,theseD(C)arealsocomponentsofSC.
Inparticular,theyaredisjointfordierentC.
Thus,eachD(C)willalsobeacomponentofSiC,whereSiisthecurrentsurfaceafteranysurgeryperformedonthecirclesinC1andinsideD(C)forsomeC=C.
GivenaxedcircleC∈C22,letSbethesurfaceobtainedfromD(C)bycappingitshole.
SinceCdoesnotboundadiscinSthatisdisjointfromD0,weknowthatSisnotasphereandhencecontainsanon-separatingcircleC(LemmaB.
1).
WechooseCsothatitavoidsthecapweaddedtoformS,i.
e.
sothatCSC.
ThenCisalsonon-separatinginthecurrentsurfaceSi(sinceeverypointofSiCcanbejoinedbyanarcinSiCtoC,whichisconnected),andwemayselectCasacircleCitocutalong.
ItremainstoselectatleasthalfofthecirclesinC12ascirclesCitocutalong.
Webeginbyselectingallthosewhoseentirestripneighbourhoods(i.
e.
,boththeir'sides')lieinD0.
(InFigureB.
1,thesearethecirclesC2andC3.
)ThesecirclesCarenon-separatingalsointhesurfaceSicurrentbeforetheyarecut,becauseD0willlieinsideacomponentofSiC.
EveryotherC∈C12liesintheclosurealsoofacomponentD(C)=D0ofSC.
(InFigureB.
1,thesearethecirclesC4,C8.
)ForeverycomponentDofSCweselectallbutoneofthecirclesC∈C12withD(C)=DasacuttingcircleCi.
Clearly,eachoftheseCiwillbenon-separatingalsoinitscurrentsurfaceSi,andtheirtotalnumberatleast|C12|/2.
HintsforalltheExercisesAtthispointinthebookthereusedtobeacollectionofhintsforalltheexercises.
Theirintentionwastohelpthosewhohadalreadyspentsometimeoveranexercisebutsomehowfailedtomakeprogress,byputtingthemontherighttrack.
Inordertonotspoilthefunofanexercise,oritsusabilityinclass,Itriedtodesignthesehintssoastomakethemsomewhatunintelligibletothosethathadnotmadesuchaninitialattemptoftheirown.
However,thisisatrickybrief,andinsomecasesthehintswillinvariablystillgiveawaysomekeyideas,ornarrowastudent'smindinpursuitofalternatives.
Itthereforeseemedbesttoleavethedecisionofwhichhintstoincludetothelecturersettingtheproblems.
TheHintssectionstillexists,andisregularlyupdated.
Asofthisftheditionofthebook,however,IhaverelegatedittotheProfessionaleBookedition.
Thisisavailabletolecturersandprofessionalmathemati-ciansviahttp://diestel-graph-theory.
com/and,foriPadusers,fromthebook'sdedicatediOSapp,GraphTheory.
(Thisgivescontinuedaccesstoearliereditionstoo,whichcontainsomeproofsnolongerincludedinlatereditions.
)Iapologizetothosereadersthatareusingthebookforself-studyandwouldhavelikedapeekatahinteverynowandthentoo.
.
.
.
R.
Diestel,GraphTheory,GraduateTextsinMathematics173,DOI10.
1007/978-3-662-53622-3ReinhardDiestel2017407IndexPagenumbersinitalicsrefertodenitions;inthecaseofauthornames,theyrefertotheoremsduetothatauthor.
Thealphabeticalorderignoreslettersthatstandasvariables;forexample,'k-chromatic'islistedundertheletterc.
above,15abstractdual,112–113,116graph,3,89,92,98,332acyclic,13–14,49,144adhesion,352,373adjacencymatrix,27adjacent,3Aharoni,R.
,57,232,238,240,241,275,276,277,278Ahuja,R.
K.
,171algebraiccolouringtheory,147owtheory,154–169,171graphtheory,23–27,34planaritycriteria,107–109algorithmicgraphtheory,171,381,390–391almost,332,342,343Alon,N.
,10,34,130,147,344alternatingpath,36,239–240walk,68ambientgraph,354Andreae,Th.
,222,275,276antichain,53,56,266,348antihole,137apexvertices,372,387Appel,K.
,146–147arboricity,48–51,123,202,252andcolouringnumber,143arc,90,249,270,278–279,280,281,399-component,249-connected,249,269jumping,248Archdeacon,D.
,390Arnborg,S.
,390articulationpoint,seecutvertexAsratian,A.
S.
,309at,2augmentingpathformatching,36,53,240,267fornetworkow,153,169automorphism,3,31,230,264averagedegree,5bounded,305andchoicenumber,130andchromaticnumber,125,130,180,183,202andconnectivity,12forcingminors,173,180–182,202,204–207forcingtopologicalminors,180–182andgirth,8,9–10,331andlistcolouring,130andminimumdegree,5–6andnumberofedges,5andRamseynumbers,305andregularitylemma,187–188,204R.
Diestel,GraphTheory,GraduateTextsinMathematics173,DOI10.
1007/978-3-662-53622-3ReinhardDiestel2017409410Indexavoid,361Babson,E.
,148back-and-forthtechnique,229,230badsequence,348,388balanced,56,341Bauer,321Behzad,M.
,148Bellenbaum,P.
,389below,15Berge,C.
,137Berger,E.
,232,279Bernstein,238between,6,90Biggs,N.
L.
,34binarytree,218,267bipartitegraphs,17–18,32,115,119,135edgecolouringof,127,144,145ownumberofcubic,160forcedassubgraph,179,195list-chromaticindexof,132–134,148matchingin,35–41,238–240inRamseytheory,295–296,304Birkho,G.
D.
,147block,60,142k-block,354graph,61,83B¨ohme,T.
,86,205Bollobas,B.
,85,86,204,205,206,275,305,321,334,336,341,344,391bond,24,32,60,111–113,118-cycleduality,25,111–113,162–164space,seecutspaceBondy,J.
A.
,321boundarycircle,399ofaface,92–94,115,116,401map,34,116ofawave,233boundedsubsetofR2,92,399boundedgraphconjecture,274χ-bounded,142Bowler,N.
,48,50,57,274,275bramble,355–359,385,386,388,389number,359orderof,355branchdecomposition(rephrased),359set,19intree-decomposition,359vertex,19Brandt,S.
,204bridge,11,43,151,161,165–167Broersma,321Brooks,R.
L.
,123,143theorem,123,147listcolouringversion,148Bruhn,H.
,118,274,275,277,279,280,311,321Burr,S.
A.
,305Cameron,P.
J.
,276Cantor,238set,268capacity,152function,151cardinality,393Carmesin,J.
,48,50,57,274,275,388,390Catlin,P.
A.
,206Cayley,A.
,147,343centralfaceingrid,375vertex,9,375centre,18certicate,135,374,391chain,15,53,58,266,394,396exchangechain,50Chebyshevinequality,337Cherlin,G.
,276choicenumber,130,144,145andaveragedegree,130ofbipartiteplanargraphs,145ofplanargraphs,130,144k-choosable,130chordofcycle,8ofspanningtree,14chordal,135–136,145,353,384k-chromatic,119,143chromaticindex,120,127ofbipartitegraphs,127vs.
list-chromaticindex,130,132andmaximumdegree,129–130chromaticnumber,119,143,164,215,273,387andKr-subgraphs,125,135,241ofalmostallgraphs,334andaveragedegree,125–126,130,180,183,202vs.
choicenumber,130andcolouringnumber,123andconnectivity,125,147constructions,126–127,144,147inextremalgraphtheory,179andownumber,164Index411forcingminors,183–187,202,203,206–207forcingshortcycles,124,331forcingsubgraphs,125,262,303forcingatriangle,144,303andgirth,125,147,187,331asaglobalphenomenon,125,135andmaximumdegree,123andminimumdegree,123,125andnumberofedges,122chromaticpolynomial,143,172Chudnovsky,M.
,137,142,148,305Chung,F.
R.
K,34Chvatal,V.
,288,309,310,312,321circleboundarycircle,399ingraphwithends,113,250,399Hamilton,311,319,321,322one/two-sided,400insurface,381,399,400,403unitcircleS1,399circuit,24,250,269–272circulation,150–151,163,170circumference,8,385andconnectivity,308andminimumdegree,8class1vs.
class2,129classicationofsurfaces,399–400cliquenumber,135–142,295closedunderaddition,154,254underinnitesums,254underisomorphism,3,332,369wrt.
minors,145,170,275,369,374,382,385wrt.
subgraphs,135,145wrt.
supergraphs,135,336upordown,intree-order,15walk,10closure(ofaset),246coboundarymap,34k-colourable,119,129–130,215,353colourclass,119colour-critical,seecriticallyk-chromaticcolouring,119–148,184,215algorithms,122,143andows,162–165number,122,143,145,247,274planegraphs,120–121,162–165inRamseytheory,285total,145,1483-colourtheorem,seethreecolourthm.
4-colourtheorem,seefourcolourthm.
5-colourtheorem,seevecolourthm.
comb,210,268modied,265star-comblemma,219combinatorialisomorphism,99,99,116settheory,273,305Comfort,W.
W.
,273compact,215,246,268compactnessprinciple,397,216,274prooftechnique,214–216,252–261,263,274fortree-width,387comparabilitygraph,135,145,146complementofabipartitegraph,135,145ofagraph,4andperfection,137–138ofaproperty,369,374–375completebipartitegraph,17graph,3,160innitegraph,211,373matching,see1-factorminor,103,107,180–187,202,203,205–207,373,380–382multipartitegraph,17,177partofpath-decomposition,385partoftree-decomposition,353r-partitegraph,17separator,353,384subgraph,125,135–136,173–177,353topologicalminor,75,86,103,107,117,180–182,184,185,187,202,207complexitytheory,135,382,391component,11,399arc-,249connected,10arc-connected,249,269,2782-connectedgraphs,59–61,83,95,100,302,3143-connectedgraphs,62–66,83,95,103–104,109,301,3024-connectedgraphs,116,301,302,311k-connected,11,12–13,72,83externally,359innitelyconnected,211,262,274locally,269minimallyconnected,14minimallyk-connected,85strongly(indigraphs),32topologically,249412Indextree-decomposition,360tree-width,360,384,385andvertexenumeration,10,14connectedness,10,14connectivity,12,10–13,59–86andaveragedegree,12andchromaticnumber,124–125,147andedge-connectivity,12inambientgraph,343,373andgirth,262,331andHamiltoncycles,310–311,320,321,322ininnitegraphs,239–241forcingminors,387andlinkability,75–76,85,87andminimumdegree,13,279andplaneduality,116andplanerepresentation,102andRamseyproperties,300–302ofarandomgraph,333viaspanningtrees,48,58consistentorientedseparations,361k-constructible,126–127,144,147–148contains,3continuum,269continuummany,393contraction,19–22and3-connectedness,62–65map,19,31minor,19inmultigraphs,28–30,170andtree-width,353convexdrawing,105,114,117polygon,303Corneil,D.
G.
,390Cornuejols,G.
,148countablegraph,2set,393countablyinnite,393coverbyantichains,55–56ofabramble,355bychains,53bycycles,115,170double,115byedges,145bypaths,52–54,238bytrees,48–51,113,117,278byvertices,35,36,45–47,355,370criticalk-chromatic,123,143factor-,43,240,263crosscap,400,402cross-edges,24,48,252crossesingrid,356crown,301–302cubed-dimensional,30,343ofagraph,G3,320cubicgraph,51-factorin,43,55ownumberof,160,161,167,171,172multigraph,46,55,167cu,372Curran,S.
,58cut,24capacityof,152,153-cycleduality,25,111–113,162–164-edge,seebridgeeven/odd,254,272,280owacross,151fundamental,26,32,254,271minimal,24,60,111innetwork,152space,25–28,32,107,112,271,280cutvertex,11,60cycle,8-bondduality,26,111–113,162–164directed,144,145disjointcycles,45–47doublecover,115,166,170edge-disjointcycles,202,262,303expectednumber,328facial,107fundamental,26,32geodesic,32,360Hamilton,170,307–322innite,311,319induced,8,65–66,95,109,136,136,271innite,113,250,279,311length,8long,8,30,84,143inmultigraphs,29non-separating,65,95,109,271odd,18,123,137withorientation,162–164short,10,124,182–183,329–331space,24–28,32,65–66,107–109,112,115,254–257,271,279,280topological,254–257,279,280thresholdfunction,341,342,343cyclomaticnumber,24cylinder,400Index413Czipszer,J.
,279Dean,N.
,321deBruijn,N.
G.
,215,274decomposition,see:edge-decomposition.
.
.
tree-decomposition.
.
.
packing.
.
.
degeneracy,seecolouringnumberdegree,5ofanend,218,247,247,279ataloop,29sequence,311deletion,4Δ-system,303densegraphs,174,177,178linearorder,265densityedgedensity,174ofpairofvertexsets,187upperdensity,201depth-rstsearchtree,16,31Deuber,W.
,291,305diameter,8–9,342andgirth,9andradius,9Diestel,R.
,118,205,206,231,244,247,252,255,256,259,273–280,354,367,373,374,388–391dierenceofgraphs,4,92digon,seedoubleedgedigraph,seedirectedgraphDilworth,R.
P.
,53,56,266Dirac,G.
A.
,206,308directedcycle,144,145edge,28graph,28,52,133,144,276path,52,143direction,150disc,399disconnected,10disjointgraphs,3dispersed,264distance,8dominateanend,263,264doublecounting,117,139–140,327,338cover,115,170edge,29,110ray,210,265,280,321wheel,301down(-closureetc.
),15drawing,2,89,98convex,105,117straight-line,105,114dualabstract,112–113,116,117andconnectivity,116plane,110–111,116,117dualitycyclesandbonds,26–28,111–113,156owsandcolourings,162–165forinnitegraphs,113,117,118ofplanemultigraphs,110–113tree-decompositionsandbrambles,356,359duplicatingavertex,137edge,2crossingapartition,24deletion,62directed,28double,29ofamultigraph,28plane,90topological,245X–Yedge,2edge-chromaticnumber,seechromaticindexedgecolouring,120,127–129,285,291andownumber,160andmatchings,144-edge-connected,12edge-connectivity,12,48,72,143,160,211edgecontraction,19and3-connectedness,62vs.
minors,19inmultigraph,29edgecover,49,145edge-decomposition,49intocircuits,24,254,280intoconnectedsubgraphs,49intoforests,50edgedensity,5,6,174andaveragedegree,5forcingminors,182forcingpathlinkages,76–82forcingsubgraphs,174–179forcingtopologicalminors,181andregularitylemma,187–188,204,207edge-disjointspanningtrees,48–52,55,211edge-end,264,273414Indexedge-maximal,4vs.
extremal,175,185withoutIK5,185,186withoutTK3,3,203withoutTK4,184–185withoutTK5,TK3,3,106edgespace,23,32,107,254Edmonds,J.
,57,240,391embeddingofbipartitegraphs,296–297ofgraphs,21k-nearembedding,372intheplane,98,100–118inS2,91–92,98self-embedding,381insurface,97,117,372–382,387,391,401emptygraph,2,11enddegree,218,247,264,278–279insubspaces,247,247,278–279ofedge,2,28-faithfulspanningtree,268ofgraph,52,113,209,217–218,219–227,245–273,278–279ofpath,6space,268thick/thin,223–227,264oftopologicalspace,269endpointsofarc,90,247endvertex,2,6terminalvertex,28enumeration,393equivalenceindenitionofanend,217,269ofgraphinvariants,202ofgraphproperties,302ofplanarembeddings,98–102,113,114ofpointsintopologicalspace,90,399inquasi-order,382Erdos,P.
,47,57,125,147,178,179,197,204,206,207,215,228,231,232,273,274,275,276,279,291,303,305,309,321,323–324,326,329–331,335,341,344Erdos-Hajnalconjecture,148,285,305Erdos-Mengerconjecture,232,276–277Erdos-Posaproperty,46,55,370–371,386,387Erdos-Posatheorem,47,57edgeversion,202,303generalization,370–371inniteversion,264Erdos-Sosconjecture,179,202,204Erdos-Stonetheorem,174,178–179,197–198,204Euler,L.
,22,33,97characteristic,401formula,97–98,114,401genus,376,401–403tour,22,272Euleriangraph,22innite,272,279evendegree,22,24,41graph,160,161,170,279event,325evolutionofrandomgraphs,342,344exactsequence,115exceptionalset,188exchangechain,50excludedminors,seeforbiddenminorsexistenceproof,probabilistic,147,323,329,329–331expandingavertex,137expectation,327–329,336exteriorface,seeouterfaceexternalconnectivity,359extremalbipartitegraph,201vs.
edge-maximal,174–175,185graphtheory,180–207,279graph,174–177withoutIK5,185,186withoutTK3,3,203withoutTK4,184–185face,90,401centralface,375ofhexagonalgrid,375facialcycle,107factor,351-factor,33–45,55,239–241,263,2671-factortheorem,42,43,55,57,85,86,240,2772-factor,42k-factor,35factor-critical,43,240,263Fajtlowicz,S.
,206fan,71,263-versionofMenger'stheorem,71,263niteadhesion,373graph,2set,393tree-width,373niteintersectionproperty,216Index415nitelyseparable,264rstordersentence,333,344rstpointonfrontier,90shlemma,367vecolourtheorem,120,148,167listversion,130–131,148ve-owconjecture,166,167,171–172Fleischner,H.
,314,319,320,321ow,149–172,151–1522-ow,1593-ow,160,167,1704-ow,160–161,166–167,163,171,1726-owtheorem,167–169,171,172k-ow,157–161,165–169,170,171,172H-ow,154–159,169-colouringduality,162–165conjectures,166–167,171,172group-valued,154–159,171–172integral,152,154networkow,151–154,169,171number,157–161,165,170inplanegraphs,162–165polynomial,156,159,171totalvalueof,152football,114forbiddenminorsandchromaticnumber,183–187expressedby,369,374–382ininnitegraphs,231,273,274,373–374minimalsetof,373,374,385,390planar,342andtree-width,355–373forciblyhamiltonian,seehamiltoniansequenceforcingIKr,180–187,205–206,373,387IK0,373–374,387TK5,186,206TKr,75,181–182,184,187,205–206edge-disjointspanningtrees,48Hamiltoncycles,308–311,314,319,320,321,322highconnectivity,12inducedtrees,179largechromaticnumber,126–127linkability,75–77,87longcycles,8,30,84,143,307–322longpaths,8,30minorwithlargeminimumdegree,182,205shortcycles,10,182–183,187,331subgraph,15,173–179,187–207tree,15,179triangle,144,303Ford,L.
R.
Jr.
,153,171forest,13,184,369minor,390partitions,51–52,57,264plane,94,113topological,264tree-widthof,369,384fourcolourproblem,147,206fourcolourtheorem,120,166,171,183–184,185,203,311,320history,147four-owconjecture,166–166Fra¨sse,R.
,276Frank,A.
,85,171Freudenthal,H.
,277compactication,246,277ends,269from.
.
.
to,6frontier,90,399Fulkerson,D.
R.
,153,171fullerene,113–114fundamentalcircuit,254,254,271cut,26,32,254,271Gale,D.
,38Gallai,T.
,33,45,52,56,57,58,86,204,263,279Gallai-Edmondsmatchingtheorem,43–45,57,238,277Galvin,F.
,134,148Gasparian,G.
S.
,137,148Geelen,J.
,391generated,254genusEulergenus,376,401–403ofagraph,387orientable,387ofasurface,381geodesic,360cycle,32,360geometricdual,seeplanedualGeorgakopoulos,A.
,278,279–280,319Gibbons,A.
,171Gilmore,P.
C.
,146girth,8andaveragedegree,8–9,331andchromaticnumber,125,147,329–331andconnectivity,87,262,331anddiameter,9416Indexandminimumdegree,8,10,30,182,331andminors,182–183,203,205andplanarity,262andtopologicalminors,183,187Godsil,C.
,34Golumbic,M.
C.
,148goodcharacterization,374,391pair,348,380sequence,348Gorbunov,K.
Yu.
,390G¨odel'scompactnesstheorem,274G¨oring,F.
,86Graham,R.
L.
,304graph,2–4,27–28,30homogeneous,230,265,276invariant,3,30,202,327minortheorem,347,380–381,374,388,389,390fortrees,349–350partition,52plane,90–98,110–113,120–121,131–132,162–165process,345property,3,228,302,332,342,343,369,374,391simple,30universal,228–231,228,265,276graphicsequence,seedegreesequencegraph-theoreticalisomorphism,99greedyalgorithm,122,133,142,143grid,114,223,356canonicalsubgrid,376hexagonalgrid,223,224,375–380minor,265,359,370,387theorem,370tree-widthof,359,384,388Grohe,M,373,391Gr¨otzsch,H.
,121,147,167,171group-valuedow,154–159,171–172Gr¨unwald,T.
,seeGallaiGuseld,D.
,57Guthrie,F.
,146Gyarfas,A.
,148,179,207Hadwiger,H.
,184,205,206conjecture,183–187,203,205,206inniteanalogue,262,274Hajnal,A.
,273,274,275,279,291,304,305Hajos,G.
,126,147,187conjecture,187,205construction,126–127Haken,W.
,146–147Halin,R.
,85,86,221,223,273,274,275,278,388,391Hall,P.
,38,54,56,238Hamilton,W.
R.
,320Hamiltoncircle,311,319,321,322Hamiltoncycle,307–322inG2,314–319inG3,320inalmostallgraphs,342anddegreesequence,311–313,320andthefourcolourtheorem,311and4-ows,170,311ininnitegraph,seeHamiltoncircleinlinegraphs,322andminimumdegree,308inplanargraphs,311powerof,319sucientconditions,307–313Hamiltonpath,307,313,319,320hamiltoniangraph,307sequence,312handle,400,402Harant,J.
,86head,seeterminalvertexHeawood,P.
J.
,147,170Heesch,H.
,147height,15hexagonalgrid,223,224,375–380Higman,D.
G.
,348,388Homan,A.
J.
,146hole,137Holz,M.
,277homogeneousgraphs,230,265,276homomorphism,3,145Hoory,S.
,10,34Huck,A.
,274hypergraph,28incidence,2encodingofplanarembedding,seecombinatorialisomorphismmap,29matrix,27,33,34poset,109incident,2,92incomparabilitygraph,267increasingproperty,336,343independencenumber,135–142andconnectivity,308–309andcovers,52,55andHamiltoncycles,308–309andlongcycles,143Index417andperfection,140ofrandomgraph,326,342independentedges,3,33–45,55events,325paths,7,71–73vertices,3,52,133,326indicatorrandomvariable,328inducedsubgraph,3–4,72,135–136,136,140ofalmostallgraphs,332,343cycle,8,32,65,66,95,109,136,13,279ofallimperfectgraphs,137,145ofalllargeconnectedgraphs,300inRamseytheory,284,290–300,303inrandomgraph,326,343tree,179,202inductiontransnite,213–214,395Zorn'sLemma,212,262,396inductiveordering,213innitegraphs,2,20,32,54,118,201,209–281,284,311,319,321,322,334,335373–374,381,388,390,391sequenceofsteps,211,221set,393basicproperties,211–212innitelyconnected,211,262innitylemma,215,274generalized,215,274,396initialsegment,394vertex,28innerface,90point,245vertex,6,13integralow,152,154function,152interiorofanarc,90ofapath,P,6–7internallydisjoint,seeindependentintersection,3graph,384intervalgraph,135,145,385into(fortree-decompositions),351invariant,3irreduciblegraph,384Irving,R.
W.
,57isolatedvertex,5,343isomorphic,3isomorphism,3ofplanegraphs,98–102isthmus,seebridgeItai,A.
,58Jaeger,F.
,171Janson,S.
,344Jensen,T.
R.
,146,172,390Johnson,D.
,373join,2Jonsson,B.
,276Jordan,C.
,90,92Jordancurvetheorem,90,117jumpingarclemma,248Jung,H.
A.
,75,206,220,264,275Khachatrian,N.
K.
,309Kahn,J.
,148Karonski,M.
,344Kawarabayashi,K.
,205,390Kelmans,A.
K.
,109,118Kempe,A.
B.
,147,321kernelofdirectedgraph,133,145ofincidencematrix,27Kirchho'slaw,149,150Kleitman,D.
J.
,147knotlessgraph,382knottheory,172Kochol,M.
,159,171Kollar,J.
,204Komlos,J.
,204,205,207,305,319,322K¨onig,D.
,35,56,127,215,274dualitytheorem,35,52,54,56,68,135,145,239innitylemma,215,274K¨onigsbergbridges,22Korman,V.
,241Kostochka,A.
V.
,182,205,305Kozlov,D.
,148Kriesell,M.
,56Krivelevich,M.
,207Kruskal,J.
B.
,349,388K¨uhn,D.
,87,183,187,205,206–207,231,276–280Kuratowski,C.
,102–107,117,263,390-theoremforhighersurfaces,375-typecharacterization,114,125,302,374,390–391Kuratowskisetofgraphs,374,390ofgraphproperties,302418IndexLachlan,A.
H.
,230,276Laplacian,34largewave,233Larman,D.
G.
,75Latinsquare,144Laviolette,F.
,280Leader,I.
B.
,274,275leaf,13,15,30,219leantree-decomposition,359Lee,O.
,58lengthofacycle,8ofapath,6,8ofawalk,10level,15liftinganedge,315limit,214–215,394wave,234line(edge),2graph,4,120,145,203,322segment,90linearalgebra,23–28,107–109,141decomposition,372programming,171Linial,N.
,10,34linkable,234linkedbyanarc,90byapath,6k-linked,74–82,85,87,181vs.
k-connected,74–76,85,87tree-decomposition,359vertices,6,90list-chromaticindex,130,132–134,144,148-chromaticnumber,seechoicenum-bercolouring,130–134,148bipartitegraphs,132–134,145Brooks'stheorem,148conjecture,132,145,148k-list-colourable,seek-choosableLiu,X.
,148Lloyd,E.
K.
,34locallynite,210,273–281locallyconnected,269logarithms,1loop,28Lovasz,L.
,56,137–138,140,147,148,204Luczak,T.
,344,345MacLane,S.
,107,117,118Mader,W.
,12,33,72,86,87,182,205,206,388Magnanti,T.
L.
,171Maharry,J.
,205Mani,P.
,75mapcolouring,119–121,142,143,146–147,162Markovchain,345Markov'sinequality,329,329,336marriagetheorem,37–38,40,54,56–57,238–239,263stable,40,56–57,134Marx,D.
,373matchable,43,239matching,35–57inbipartitegraphs,34–41,135andedgecolouring,144ingeneralgraphs,39–45ininnitegraphs,239–241,267,277partial,239,267stable,40,55,134ofvertexset,35Mate,A.
,273,305matroid,57,58,118,391innite,274,280max-owmin-cuttheorem,151,153,169,171maximal,4acyclicgraph,14element,394,396planargraph,102,107,114,115,117,186,203planegraph,94,102wave,234maximumdegree,5bounded,196–197,288andchromaticnumber,123andchromaticindex,127–130andlist-chromaticindex,134,148andradius,9andRamseynumbers,288–289andtotalchromaticnumber,145Mazoit,F.
,389Menger,K.
,56,66–71,84,86,169,221,239–241,266,276–277theoremof,66–71,84,86,169,221–222,231,232,263,276–277metrizable,247,269Milgram,A.
N.
,52,56,58Milner,E.
C.
,275minimal,4connectedgraph,14k-connectedgraph,85Index419cut,24,60,111,156element,394non-planargraph,114separator,82–83setofforbiddenminors,374,385,390minimumdegree,5andaveragedegree,5andchoicenumber,130–131andchromaticnumber,123,125andcircumference,8andconnectivity,13,86,279andedge-connectivity,12forcingHamiltoncycle,308,319forcinglongcycles,8forcinglongpaths,8,30forcingshortcycles,10,182–183,187,331forcingtrees,15andgirth,8,9,10,182–183,205,331andlinkability,76minor,19–22,19,180–183K3,3,117,203K4,184–185,369–370K5,185,186,206,384K5andK3,3,102–107K6,186Kr,181,182,183,184,202,203,205–207,343,373,387K0,373–374,387ofalllarge3-or4-connectedgraphs,301–302-closedgraphproperty,369,374–382,385contraction,20excluded,seeforbiddenforbidden,183–187,231,274,369–382,385,388–391forced,182,184,180–187incomplete,205innite,211,222–223,231,264,275,276,277,279,387,390model,19ofmultigraph,29Petersengraph,166andplanarity,102–107,114proper,381relation,20,32,222,231,265,276,302,355,374theorem,347,374–382,374,390–391proof,374–381fortrees,349–350vs.
topologicalminor,20–22,103andWQO,347–391(seealsotopologicalminor)M¨obiuscrown,301–302ladder,186strip,400modelofaminor,19Mohar,B.
,117,147,205,391momentrst,seeMarkov'sinequalitysecond,335–342monochromatic(inRamseytheory)inducedsubgraph,289–300(vertex)set,286–287subgraph,285,287–289Moorebound,10,34M¨uller,Th.
,389multigraph,28–30cubic,46,55,166listchromaticindexof,148plane,110multipleedge,28Murty,U.
S.
R.
,321Myers,J.
S.
,205Nash-Williams,C.
St.
J.
A.
,48,51,57,252,273,276,278,280,321,388k-nearembedding,372nearlyplanar,373Negami,S.
,86Negropontis,S.
,273neighbourofasetofvertices,5ofavertex,3Neˇsetˇril,J.
,304,305nestedseparations,367,384network,151–154theory,171Niedermeyer,F.
,274,277node(vertex),2normaltree,15–17,31,165,170,303ininnitegraphs,220,247,254,264,269,278,374,391ray220,264nowheredense,49zero,154,171null,seeemptyobstructiontosmalltree-width,355–359,367octahedron,12,17,390oddcomponent,41,263420Indexcycle,18,123,137,144,145,148degree,5,320on,2one-factortheorem,42,57,86,240openEulertour,272Oporowski,B.
,301,305,388orderofabramble,355ofagraph,2partial,15,20,31,32,52–54,56,145,382,393,394,396quasi-,348ofaseparation,11,360tree-,15,31type,394well-quasi-,347–349,374,382,383,388ordinal,394–395orientablesurface,387planeas,157orientationacyclic,143ofacycle,162–163ofaedge,150ofagraph,28,133,143,171,202ofaseparation,361Orlin,J.
B.
,171orthogonalsubspaces,25Osthus,D.
,87,183,187,205,206–207outerface,90,99–100,115outerplanar,115,385over,362Oxley,J.
G.
,118,278,301,305Oxtoby,J.
C.
,273packing,35,45–52,252,263-coveringtheorem,49,263,272tree-,49Palmer,E.
M.
,344paralleledges,29parity,5,41,44partoftree-decomposition,351partiallyorderedset,52–54,56,269,394,396r-partite,17partition,1,51,285edge,49pass,315pasting,136,184,185,203,353,384path,6–10,210a–b-path,7,71A–B-path,7,63–71,84,231–238,262H-path,7,63,72–73,84alternating,36–37,38,68betweengivenpairsofvertices,74–82-connected,278cover,52–54,52,238-decomposition,372,385directed,52,143disjointpaths,52,62–71,74–82,231–237edge-disjoint,48,71,73-hamiltoniansequence,313independentpaths,7,71,72–73,84,85induced,302length,6linkage,74–82,87long,8-width,385,390perfect,135–142,145,148,241graphconjectures,137graphtheorems,137,137,145,148matching,see1-factorstrongly,241,267weakly,241,267Petersen,J.
,43Petersengraph,166piecewiselinear,89planar,102–117,120–121,131,231,370,371,373embedding,98,102–117nearlyplanar,373planaritycriteriaKelmans,109Kuratowski,107MacLane,107Tutte,117–118Whitney,113planedual,110duality,110–113,135,117,156–165graph,90–98multigraph,110–113,116,117,156–165triangulation,96,97,170,353Platonicsolid,113–114Plummer,M.
D.
,56Podewski,K.
P.
,277point(vertex),2pointwisegreater,312Polat,N.
,278polygon,90polygonalarc,90,91Posa,L.
,47,57,291,305powerofagraph,314,320set,393Index421predecessor,394preferences,40,54,134Prikry,K.
,275probabilisticmethod,323,329–331,344projectiveplane,390properminor,381separation,11subgraph,3wave,233property,3,302,332ofalmostallgraphs,332–335,341–342equivalence,302increasing,336minor-closed,369,385non-trivial,302Proskurowski,A.
,390pruning,242pseudo-randomgraph,304Pym,J.
S.
,238,277quasi-ordering,347–349,374,382,383,388radius,9anddiameter,9,30andmaximumdegree,9Rado,R.
,56,273,276,305graph,229–230,265,276,334,335Rado'sselectionlemma,274Ramsey,F.
P.
,284–287Ramseygraph,290-minimal,296–297numbers,285,287,303,305,326,344Ramseytheory,267–305andconnectivity,300–302induced,297–300innite,286,303,304randomgraph,175,187,287,344–345,325evolution,342,344innite,334process,345uniformmodel,344,345randomvariable,327indicatorr.
v.
,328rank,243ray,210,215,219,221,261,264,265,269,374double,210,265,275,280,321normal220,264spanning,321rayless,214,243ranking,243recursivedenitions,242–244pruningoftrees,242reducibleconguration,147Reed,B.
A.
,57,388reningapartition,1,190–193region,90–92onS2,92regular,5,39,41,144,319-regularpair,187,203forsparsegraphs,207partition,188regularitygraph,196inated,Rs,288lemma,174,187–200,188,204,304forsparsegraphs,207Reiher,C.
,204,274Renyi,A.
,228,276,335,341,344Richardson,M.
,145Richter,B.
,391rigid-circuit,seechordalring,375,376Robertson,N.
,57,137,147,148,172,186,206,355,370,372,374,388–390,391R¨odl,V.
,288,291,305Ronyai,L.
,204root,15rootedtree,15,349,383Rothschild,B.
L.
,304Royle,G.
F.
,34Rucinski,A.
,344Salazar,G.
,391Sanders,D.
P.
,147Sark¨ozy,G.
N.
,319,322saturated,seeedge-maximalSauer,N.
,276Schnyder,W.
,109Schoenies,A.
M.
,90Schrijver,A.
,56,57,85,86,148,171Schmidt,R.
,277Schur,I.
,303Scott,A.
D.
,142,207,276secondmoment,335–342,337self-minorconjecture,381,387,388separateagraph,11,67,72theplane,90422Indexseparatingcircle,400,403separation,11corner,363crossing,363nested,384orderof,11oriented,361inducedbyatree-decompositions,352,361,367,384,386starof,361submodularity,363separator,11sequentialcolouring,seegreedyalgo-rithmseries-parallel,203setk-set,1countable,393countablyinnite,393nite,393innite,393powerset,393system,seehypergraphwell-founded,394Seymour,P.
D.
,57,86,137,142,147,148,148,167,172,186,206,319,322,355,355,370,371,372,374,381,388,389,390,391Shapley,L.
S.
,38Shelah,S.
,274,275,276,277Shi,N.
,276sideofacut,24Simonovits,M.
,57,204,207,305simple,30simplicialtree-decomposition,259,353,384,388six-owtheorem,167,172smallwave,233snark,166planar,166,171,311Sos,V.
,179,202,204spannedsubgraph,4spanningray,321astandardsubspace,247subgraph,4trees,14,16edge-disjoint,48–52end-faithful,268normal,15–17,31,220,247,254,264,268,275,374,391numberof,343topological,instandardsubspaces,271topological,52,250–257,269,271,280sparsebasis,107graph,173,180–183,203,207,288,305regularitylemma,207Spencer,J.
H.
,304,344Sperner,E.
,54sphereS2,92,99–100,399spine,210splittertheorem,86splittingavertex,65Spr¨ussel,Ph.
,279squareofagraph,314–319,320,321Latin,144stabilitynumber,seeindependencenumberstablemarriage,40,57,134matching,40,55,134set,3standardbasis,23subspace,246,247,249,250,253,246,269topologicalspanningtreesin,270,271star,18,202,290,302centreof,18induced,300innite,219ofseparations,361star-comblemma,219,220Steens,K.
,240,277Stein,M.
,277,279Steinitz,E.
,117stereographicprojection,92Stillwell,J.
,117Stone,A.
H.
,178,195straightlinesegment,90stripneighbourhood,94,400strong-lyconnected,32-lyperfect,241,267subcontraction,seeminorsubdividingvertex,19subdivision,19submodularityoforderofseparations,363subgraph,4ofalllargek-connectedgraphs,300–302Index423forcedbyedgedensity,174–179,187–201,202,203ofhighconnectivity,12induced,4oflargeminimumdegree,6,123,145spanning,4successor,394Sudakov,B.
,207,305sumofedgesets,23ofows,159ofthinfamilies,254supergraph,4suppressingavertex,29,46–47,64–65surface,372,375,376,399–405surgeryon402surgeryonsurfaces402capping402cutting402symmetricdierence,23,36,69systemofdistinctrepresentatives,54Szabo,T.
,204Szekeres,G.
,303Szemeredi,E.
,187,205,207288,305,319,322seealsoregularitylemmatailofanedge,seeinitialvertexofaray,210,261Tait,P.
G.
,147,321tangle,362,389–390dualitytheorem,362Tarsi,M.
,147teeth,210terminalvertex,28thick/thinend,223–227,264thinend223–227,251family,254sum,254Thomas,R.
,57,76,86,137,147,148,172,186,206,301,305,321,356,360,388–391Thomason,A.
G.
,205,336Thomasse,S.
,276Thomassen,C.
,117,131,147,148,183,205,206,277,278,321,322,390,391,403threecolourtheorem,121three-owconjecture,167thresholdfunction,335–342,343,344Toft,B.
,147,172topologicalconnectedness,247,253cyclespace,254–257,279,280edge,245enddegree,247space|G|,245–261,269Eulertour,272isomorphism,99,99,111spanningtree,52,250–257,269,271,280topologicalminor,19K3,3,98,103,106,107,117,203K4,64,184–185,203,369–370K5,98,103,106,107,117,186,206,384K5andK3,3,98,103,106,107,115,117Kr,75,175,181–183,187,202,203,207,284,300,360,373K0,211,220,264,266,374,387ofalllarge2-connectedgraphs,301forcedbyaveragedegree,181–183forcedbychromaticnumber,187forcedbygirth,183,187induced,181asorderrelation,20vs.
ordinaryminor,20,103andplanarity,98,102–107tree(induced),179andWQOofgeneralgraphs,383andWQOoftrees,349torso,352,372–373totalchromaticnumber,145totalcolouring,145conjecture,145,148totalvalueofaow,152touchingsets,355t-tough,310–311,319,320toughnessconjecture,310,319,321–322tournament,319C-trail,315transniteinduction,213–214,395transitivegraph,55travellingsalesmanproblem,320tree,13–17binary,218,267cover,48–51,113asforcedsubstructure,15,179,202levelof,15normal,15–17,31,165,170innite,220,247,254,262,264,267,275,374,391-order,15packing,48–51,57–58,263,278,279424Indexpath-widthof,385ofseparations,362spanning:seespanningtree14,16,212,221topological,52,250–257,269,271,279topologicalinstandardsubspaces,270,271thresholdfunctionfor,342well-quasi-orderingoftrees,349–350treecoveringtheorem,49,263tree-decomposition,206,351–360,372–373,383,388–389of2-connectedgraphsinto3-conn'dpieces,62,384connected,360inducedonminors,352inducedonsubgraphs,352lean,359obstructions,355–359,360partof,351simplicial,351,384,388,391widthof,355treepackingtheorem,48,252tree-width,355–373andbrambles,355–359,386,388,389compactnesstheorem,387connected,360,384dualitytheorem,356,359nite,373andforbiddenminors,369–373ofgrid,359,385,388ofaminor,355obstructionstosmall,355–359,360ofasubdivision,384triangle,3triangulated,seechordaltriangulation,seeplanetriangulationtrivialgraph,2Trotter,W.
T.
,288,305Turan,P.
,175theorem,175,204,288graph,175–180,204Tutte,W.
T.
,42,48,57,62,63,64,65,85–86,109,117–118,154,157,164,171–172,238,247,278,311,321condition,41–42cyclebasistheorem,65,2791-factortheorem,42,57,240owconjectures,166–167,171planaritycriterion,109,117polynomial,172treepackingtheorem,48,57,252,278wheeltheorem,64–65,85–86Tychono'stheorem,216,274ubiquitous,222,265,276conjecture,222,265,276unfriendlypartitionconjecture,217,263,275uniformitylemma,seeregularitylemmaunion,3unitcircleS1,90,399universalgraphs,228–231,228,265,276unmatched,35up(-closureetc.
),15upperbound,394density,201Urquhart,A.
,147valency(degree),5valueofaow,152vanderWaerden,303variance,337Veldman,H.
J.
,321vertex,2-chromaticnumber,119colouring,119,122–127-connectivity,11cover,36,52–54cut,seeseparatorduplication,137expansion,137ofaplanegraph,90space,23-transitive,55,230,264Vizing,V.
G.
,128,148Voigt,M.
,148vortex,356,387Vuˇskovic,K.
,148Wagner,K.
,107,186,203,206,388'Wagner'sConjecture',seegraphminortheoremWagnergraph,186,353,384,390walk,10alternating,68closed,10length,10wave,233,266large,233limit,234Index425maximal,234proper,233small,233weaklyperfect,241,267well-foundedset,394well-ordering,394theorem,394well-quasi-ordering,347–391Welsh,D.
J.
A.
,172wheel,65,301,302theorem,65,85–86Whitney,H.
,86,102,113widthoftree-decomposition,355Wilson,R.
J.
,34Winkler,P.
,344Wollan,P.
,76,86,390–391Woodrow,R.
E.
,230,276Yu,X.
,58,321Zehavi,A.
,57Zorn'slemma,212,262,396Zykov,A.
A.
,204SymbolIndexTheentriesinthisindexaredividedintotwogroups.
Entriesinvolvingonlymathematicalsymbols(i.
e.
nolettersexceptvariables)arelistedontherstpage,groupedlooselybylogicalfunction.
Theentry'[]',forexample,referstothedenitionofinducedsubgraphsH[U]onpage4aswellastothedenitionoffaceboundariesG[f]onpage94.
Entriesinvolvingxedlettersasconstituentpartsarelistedonthesecondpage,intypographicalgroupsorderedalphabeticallybythoseletters.
Lettersstandingasvariablesareignoredintheordering.
2:=,=:3,=33331,36320+4,23,1544,92,154.
62∈2921∪,∩34,1,15||2,152,2452,187,259[]4,94,245[]k,[]<ω1,348,23/20,29C⊥,F⊥,.
.
.
240,1,2,.
.
.
1(n)k,.
.
.
328E(v),F(w)2E(X,Y),F(U,W)2(e,x,y),(u,v)150,245→E,→F,→C,.
.
.
150,156,158←e,←E,←F,.
.
.
150f(X,Y),g(U,W)150G,F,→e,.
.
.
110,156G2,H3,.
.
.
314G,X,P,.
.
.
4,150,246,369(S,S)152xy,x1.
.
.
xk,.
.
.
2,7xP,Px,xPy,xPyQz,.
.
.
7P,xQ,F,.
.
.
7,88,245xTy,.
.
.
14R.
Diestel,GraphTheory,GraduateTextsinMathematics173,DOI10.
1007/978-3-662-53622-3ReinhardDiestel2017427428SymbolIndexE327F21,23N1,393P325Zn1Zm*Zn161CG41C(G)24,254B(G)25,265E(G)23G(n,p)324KP,KP(S)374PH338Pi,j332V(G)23Ck,C(S,ω),C(S,ω)8,245E(G)2E(X)246F(G)92Forb369G(H1,H2)291IX19Kn3,211Kn1,.
.
.
,nr17Krs17L(G)4N(v),N(U)5N+(v)211Pk6PG144R(H)287R(H1,H2)287R(k,c,r)287R(r)285Rs196Sn92,399T2218TX19Tr1(n)175V(G)2V(X)246ch(G),ch(G)130col(G)122d(v),d(G)5d+(v)133d(x,y)8d(X,Y)187diam(G)8ex(n,H)175f(v)110g(G)8i1init(e)28log,ln1pw(G)385q(G)39rad(G)9tr1(n)175ter(e)28tw(G)355ve,vxy,vU20v(f)110Δ(G)5α(G)135δ(G)5ε(G),ε,ε(S)5,339,401κ(G)12κH(G)73λ(G)12λH(G)73μ337π:S2{(0,0,1)}→R292σk:Z→Zk157σ2337(G)157χ119,401χ(G)120χ(G)145ω(G),ω135,394Ω(G)2180,1393ReinhardDiestelreceivedaPhDfromtheUniversityofCambridge,follow-ingresearch1983–86asascholarofTrinityCollegeunderBelaBollobas.
HewasaFellowofSt.
John'sCollege,Cambridge,from1986to1990.
ResearchappointmentsandscholarshipshavetakenhimtoBielefeld(Germany),OxfordandtheUS.
HebecameaprofessorinChemnitzin1994andhasheldachairatHamburgsince1999.
ReinhardDiestel'smainareaofresearchisgraphtheory,includinginnitegraphtheory.
Hehaspublishednumerouspapersandaresearchmonograph,GraphDecompositions(Oxford1990).
LetA,Bbesets.
IfthereexistsabijectivemapbetweenAandB,wewrite|A|=|B|andsaythatAandBhavethesamecardinality.
Thisisclearlyanequivalencerelationbetweensets,andwemaythinkofthecardinality|A|ofAastheequivalenceclasscontainingA.
Wewritecardinality|A||B|ifthereexistsaninjectivemapA→B.
Thisisclearlywelldened,anditisapartialordering:ifthereareinjectivemapsA→BandB→A,thereisalsoabijectionA→B.
1Foreverysetthereexistsanotherthatisbigger;forexample,|A||G|,becauseα→xαwouldbeaninjectivemapfromαtoV(G)showingthat|α||G|.
Sincethereexistordinalslargerthan|G|,suchasanyordinalequivalenttoawell-orderingofthepowersetofV(G),396AppendixAthismeansthatourrecursioncannotgoonindenitely,i.
e.
weshallnotbeabletodenexαforallordinalsα.
Wemaynotknowinadvancewhenourrecursionwillgetstuck,i.
e.
,whichisthesmallestordinalαforwhichxαcannotbefoundincompliancewithourrules.
Butthisdoesnotmatter:wesimplydeneαastherstordinalαforwhichxαcannotbefound,contentourselveswithhavingdenedxαforallαp,whicharecompatibleinthatfqpfrq=frpwheneverr>q>p.
GeneralizedInnityLemma.
Foreverysuchfamily{Xp|p∈P}ofnitesetsthereexistsafamily{xp|p∈P}ofrepresentativesxp∈Xpsuchthatfqp(xq)=xpwheneverq>p.
Theinnitylemmaisclearlyaspecialcaseofthis,withP=Nandthefqpdenedbyiteratingthelemma'spredecessorfunctionf.
2Incategorytheory,our'generalizedinnitylemma'isknownasthefactthattheinverselimitofanydirectedinversesystemofnitesetsisnon-empty.
Insteadofnitesetsonecantakeanyothercompactspaces;seeChapter8.
8foranapplication.
Innitesets397Thefollowingmorecombinatorialencodingforcompactnessargu-mentsbringsoutparticularlywellthechoicesinvolved,andtheirinter-dependence.
LetXbeanyset,Saniteset,andFasetofnitesubsetsofX.
AssumethateveryY∈FcomeswithaxedsetA(Y)ofY→Sfunctions,itsadmissiblefunctions.
CallYFcompatibleifthereexistsafunctionf:X→SallwhoserestrictionstothesetsinYareadmissible,i.
e.
whichsatisesf|Y∈A(Y)forallY∈Y.
CompactnessPrinciple.
FiscompatibleifeveryniteYFiscompatible.
TheproofsofthegeneralizedinnitylemmaandofthecompactnessprincipleareeachjustafewlinesbasedonTychono'stheoremthateveryproductofcompactspacesiscompact.
Weillustratethisforthecompactnessprinciple.
ThinkofthesetofallX→Sfunctionsasaproductof|X|copiesofS,sotheyformacompactspace.
ForeveryniteYX,thesetofallfunctionsf:X→Swithf|Y∈A(Y)isclosed(aswellasopen)inthisproductspace.
Theresultnowfollowsfromthe'niteintersectionproperty'ofcompactspaces,thatafamilyofclosedsetshasanon-emptyintersectionassoonasallitsnitesubfamiliesdo.
BSurfacesThisappendixoersasummaryofbackgroundinformationaboutsur-faces,asneededforanunderstandingoftheirroleintheproofofthegraphminortheoremortheproofofthe'generalKuratowskitheorem'forarbitrarysurfacesgiveninChapter12.
7.
Inordertobereadatarigorouslevelitrequiresfamiliaritywithsomebasicdenitionsofgeneraltopology(suchasoftheproductandtheidenticationtopology),butnomore.
Asurface,forthepurposeofthisbook,isacompactconnected1surfaceHausdortopologicalspaceSinwhicheverypointhasaneighbourhoodhomeomorphictotheEuclideanplaneR2.
Anarc,acircle,andadiscarcinSaresubsetsthatarehomeomorphicinthesubspacetopologytothecircleS1realinterval[0,1],totheunitcircleS1={x∈R2:x=1},andtodisctheunitdisc{x∈R2:x1}or{x∈R2:x<1},respectively.
ThecomponentsofasubsetXofSaretheequivalenceclassesofcomponentpointsinXwheretwopointsareequivalentiftheycanbejoinedbyanarcinX.
ThesurfaceSitself,beingconnected,hasonlyonecomponent.
ThefrontierofXisthesetofallpointsyinSsuchthateveryfrontierneighbourhoodofymeetsbothXandSX.
ThefrontierFofXseparatesSXfromX:sinceX∪Fisclosed,everyarcfromSXtoXhasarstpointinX∪F,whichmustlieinF.
AcomponentofthefrontierofXthatisacircleinSisaboundarycircleofX.
AboundaryboundarycirclecircleofadiscinSissaidtoboundthatdisc.
Thereisafundamentaltheoremaboutsurfaces,theirclassication.
Thissaysthat,uptohomeomorphism,everysurfacecanbeobtainedfromthesphereS2={x∈R3:x=1}by'addingnitelymanysphereS2handlesornitelymanycrosscaps',andthatsurfacesobtainedbyaddingdierentnumbersofhandlesorcrosscapsaredistinct.
Weshallnotneedtheclassicationtheorem,buttoformapictureletusseewhatthe1Throughoutthisappendix,'connected'means'arc-connected'.
R.
Diestel,GraphTheory,GraduateTextsinMathematics173,DOI10.
1007/978-3-662-53622-3ReinhardDiestel2017399400AppendixBaboveoperationsmean.
ToaddahandletoasurfaceS,weremovetwohandleopendiscswhoseclosuresinSaredisjoint,andidentify2theirboundarycircleswiththecirclesS1*{0}andS1*{1}ofacopyofS1*[0,1]disjointfromS.
Toaddacrosscap,weremoveoneopendisc,andthencrosscapidentifyoppositepointsonitsboundarycircleinpairs.
Inordertoseethattheseoperationsdoindeedgivenewsurfaces,wehavetocheckthateveryidenticationpointendsupwithaneigh-bourhoodhomeomorphictoR2.
Todothisrigorously,letusrstlookatcirclesmoregenerally.
AcylinderistheproductspaceS1*[0,1],oranyspacehomeomor-cylinderphictoit.
ItsmiddlecircleisthecircleS1*{12}.
AM¨obiusstripisanyspacehomeomorphictotheproductspace[0,1]*[0,1]afteridenti-M¨obiusstripcationof(1,y)with(0,1y)forally∈[0,1].
Itsmiddlecircleistheset{(x,12)|0
Ifthisstripneighbourhoodisacylinder,thenNChastwocomponentsandwecallCtwo-sided;ifitisaM¨obiusstrip,thentwo-sidedNChasonlyonecomponentandwecallCone-sided.
one-sidedUsingsmallneighbourhoodsinsideastripneighbourhoodofthe(two-sided)boundarycircleofthediscordiscsweremovedfromSinordertoattachacrosscaporhandle,onecanshoweasilythatbothoperationsdoproducenewsurfaces.
SinceSisconnected,SCcannothavemorecomponentsthanNC.
IfSChastwocomponents,wecallCaseparatingcircleinS;separatingcircleifithasonlyone,thenCisnon-separating.
Whileone-sidedcirclesareobviouslynon-separating,two-sidedcirclescanbeeitherseparatingornon-separating.
Forexample,themiddlecircleofacylinderaddedtoSasa'handle'isatwo-sidednon-separatingcircleinthenewsurfaceobtained.
WhenSisobtainedfromSbyaddingacrosscapinplaceofadiscD,theneveryarcinSthatrunshalf-wayroundtheboundarycircleofDbecomesaone-sidedcircleinS.
Theclassicationtheoremthushasthefollowingcorollary:LemmaB.
1.
Everysurfaceotherthanthespherecontainsanon-separatingcircle.
2Thisismadeprecisebytheidenticationtopology,whoseformaldenitioncanbefoundinanytopologybook.
SinceS1hastwopossibleorientations,twocopiesofS1canbeidentiedintwoessentiallydierentways.
Thecorrespondingtwowaysofaddingahandleyielddierentnewsurfaces.
Fortheclassicationoneonlyusesoneofthese,thewaythatpreservestheorientabilityofthesurface(asinFigureB.
1).
3Inprinciple,thestripneighbourhoodNisconstructedasintheproofofLemma4.
2.
2,usingthecompactnessofC.
Howeversincewearenotinapiecewiselinearsettingnow,theconstructionisconsiderablymorecomplicated.
Surfaces401Weshallseebelowthat,inasense,ourtwoexamplesofnon-separatingcirclesareallthereare:cuttingasurfacealonganynon-separatingcircle(andpatchinguptheholes)willalwaysproduceasurfacewithfewerhandlesorcrosscaps.
AnembeddingG→SofagraphGinSisamapσthatmapstheembeddingverticesofGtodistinctpointsinSanditsedgesxytoσ(x)–σ(y)arcsσ:G→SinS,sothatnoinnerpointofsuchanarcistheimageofavertexorliesonanotherarc.
Wethenwriteσ(G)fortheunionofallthosepointsandarcsinS.
AfaceofGinSisacomponentofSσ(G),andthefacesubgraphofGthatσmapstothefrontierofthisfaceisitsboundary.
boundaryNotethatwhilefacesinthespherearealwaysdiscs(ifGisconnected),ingeneraltheyneednotbe.
Onecanprovethatineverysurfaceonecanembedasuitablegraphsothateveryfacebecomesadisc.
ThefollowinggeneralversionofEuler'stheorem4.
2.
9thereforeappliestoallsurfaces:TheoremB.
2.
ForeverysurfaceSthereexistsanintegerχ(S)suchthatwheneveragraphGwithnverticesandmedgesisembeddedinSsothattherearefacesandeveryfaceisadisc,wehavenm+=χ(S).
ThisinvariantχofSisitsEulercharacteristic.
Forcomputationalsimplicityweusuallyworkinsteadwiththederivedinvariantε(S):=2χ(S),ε(S)theEulergenusofS,becauseχisnegativeformostsurfacesbutεtakesEulergenusitsvaluesinN(seebelow).
PerhapsthemoststrikingfeatureofEuler'stheoremisthatitworkswithalmostanygraphembeddedinS.
ThismakesiteasytoseehowtheEulergenusisaectedbytheadditionofahandleorcrosscap.
Indeed,letDandDbetwoopendiscsinSthatwewishtoremoveinordertoattachahandlethere.
LetGbeanygraphembeddedinSsothateveryfaceisadisc.
Ifnecessary,shiftGonSsothatDandDeachlieinsideaface,fandf,say.
AddcyclesCandContheboundarycirclesofDandD,andjointhembyanedgetotheoldboundariesoffandf,respectively.
Theneveryfaceoftheresultinggraphisagainadisc,andDandDareamongthese.
NowremoveDandD,andaddahandlewithanadditionalC–Cedgerunningalongit.
Thisoperationmakesthenewhandleintoonenewface,whichisadisc.
Itthusreducesthetotalnumberoffacesby1(sincewelostDandDbutgainedthenewfaceonthehandle)andincreasesthenumberofedgesby1,butleavesthenumberofverticesunchanged.
Asaresult,εgrowsby2.
402AppendixBSimilarly,replacingadiscDboundedbyacycleCGwithacrosscapdecreasesthenumberoffacesby1(sinceweloseD),butleavesnmunchangedifwearrangethecycleCinsuchawaythatverticesgetidentiedwithverticeswhenweidentifyoppositepoints.
Wehavethusshownthefollowing:LemmaB.
3.
(i)AddingahandletoasurfaceraisesitsEulergenusby2.
(ii)AddingacrosscaptoasurfaceraisesitsEulergenusby1.
SincethespherehasEulergenus0(Theorem4.
2.
9),theclassica-tiontheoremandLemmaB.
3tellusthatεhasallitsvaluesinN.
Wemaythustrytoprovetheoremsaboutsurfacesbyinductiononε.
Fortheinductionstep,wecouldsimplyundotheadditionofahandleorcrosscapdescribedearlier,cuttingalongthenewnon-separatingcircleitproduced(whichrunsaroundthenewhandleor'half-way'aroundthecrosscap)andrestoringtheoldsurfacebyputtingbackthediscordiscsweremoved.
Aproblemwiththisisthatwedonotnormallyknowwhereonoursurfacethiscirclelies,saywithrespecttoagivengraphembeddedinit.
However,thegenus-reducingcut-and-pasteoperationcanbecarriedoutwithanynon-separatingcircle:wedonothavetouseonethatweknowcamefromanewhandleorcrosscap.
Thisisanexampleofamoregeneraltechniqueknownassurgery,andworksasfollows.
LetCbeanon-separatingcircleinasurfaceS=S2.
TocutSalongC,weformanewspaceSfromSbyreplacingeverypointx∈Ccuttingwithtwopointsx,xanddeningthetopologyonthemodiedsetasfollows.
4LetNbeanystripneighbourhoodofCinS,andputX:={x|x∈C}andX:={x|x∈C}.
IfNisacylinder,thenNChastwocomponentsNandN,andwechoosetheneighbourhoodsofthenewpointsxandxinSsothatXandXbecomeboundarycirclesofNandNinS,respectively,andN∪XandN∪XbecomedisjointcylindersinS.
IfNisaM¨obiusstrip,wechoosetheseneighbourhoodssothatXandXeachformanarcinSandX∪XisaboundarycircleofNCinS,with(NC)∪X∪XformingonecylinderinS.
Finally,weturnSintoasurfacebycappingitsholes:cappingforeachofthe(twoorone)boundarycirclesXandXorX∪XofSCinSwetakeadiscdisjointfromSandidentifyitsboundarycirclewithX,XorX∪X,respectively,sothatthespaceobtainedisagainasurface.
4Thedescriptionthatfollowsmaysoundcomplicated,butitisnot:workinginourconcretemodelsofthecylinderandtheM¨obiusstripitiseasytowritedownexplicitneighbourhoodbasesthatdeneatopologywiththepropertiesstated.
Asallwewantistoobtainsomesurfaceofsmallergenus,wedonotcareaboutuniqueness(whichwillfollowanyhowfromLemmaB.
4andtheclassication).
Surfaces403ComputinghowtheseoperationsaecttheEulergenusofSisagaineasy,assumingwecanembedagraphinSsothateveryfaceisadiscandCistheimageofacycle.
(Thiscanalwaysbedone,butitisnoteasytoprove.
5)Indeed,bydoublingCweleftnmunchanged,becauseacyclehasthesamenumberofverticesasedges.
Soallwechangedwas,whichincreasedby2intherstcaseandby1inthesecond.
LemmaB.
4.
LetCbeanynon-separatingcircleinasurfaceS,andletSbeobtainedfromSbycuttingalongCandcappingtheholeorholes.
(i)IfCisone-sidedinS,thenε(S)=ε(S)1.
(ii)IfCistwo-sidedinS,thenε(S)=ε(S)2.
LemmaB.
4givesusalargesupplyofcirclestocutalonginaninductionontheEulergenus.
Still,itissometimesmoreconvenienttocutalongaseparatingcircle,andmanyofthesecanbeusedtoo:LemmaB.
5.
LetCbeaseparatingcircleinasurfaceS,andletSandSbethetwosurfacesobtainedfromSbycuttingalongCandcappingtheholes.
Thenε(S)=ε(S)+ε(S).
Inparticular,ifCdoesnotboundadiscinS,bothSandShavesmallerEulergenusthanS.
Proof.
Asbefore,embedagraphGinSsothateveryfaceisadiscandCistheimageofacycleinG,andletG→SandG→Sbethetwographsobtainedinthesurgery.
Thus,GandGbothcontainacopyofthecycleonC,whichweassumetohavekverticesandedges.
Then,withtheobviousnotation,wehaveε(S)+ε(S)=(2n+m)+(2n+m)=4(n+k)+(m+k)(+2)=2n+m=ε(S).
NowifS(say)isasphere,thenS∩SwasadiscinSboundedbyC.
Hence,ifCdoesnotboundadiscinSthenε(S)andε(S)arebothnon-zero,givingthesecondstatementofthelemma.
WenowapplythesetechniquestoprovealemmaforourdirectproofinChapter12ofthe'Kuratowskitheoremforarbitrarysurfaces',Corollary12.
7.
3.
5PerhapsthesimplestproofwasgivenbyC.
Thomassen,TheJordan-Schoeniestheoremandtheclassicationofsurfaces,Amer.
Math.
Monthly99(1992),116–130.
404AppendixBLemmaB.
6.
LetSbeasurface,andletCbeanitesetofdisjoint[12.
7.
4]circlesinS.
AssumethatSChasacomponentD0whoseclosureinSmeetseverycircleinC,andthatnocircleinCboundsadiscinSthatisdisjointfromD0.
Thenε(S)|C|.
Proof.
WebeginwiththeobservationthattheclosureofD0notonlymeetsbutevencontainseverycircleC∈C.
ThisisbecauseChasastripneighbourhoodNdisjointfromalltheothercirclesinC(sincetheirunioniscompact),andeachofthe(oneortwo)componentsofNChasallofCinitsclosure.
SinceD0meets,andhencecontains,atleastonecomponentofNC,itsclosurecontainsC.
LetuspartitionCasC=C1∪C12∪C22,wherethecirclesinC1areC1,C12,C22one-sided,thoseinC12aretwo-sidedbutnon-separating,andthoseinC22areseparating.
Weshall,inturn,cutalongallthecirclesinC1,some|C22|non-separatingcirclesnotinC,andatleasthalfthecirclesinC12.
ThiswillgiveusasequenceS0,Snofsurfaces,whereS0=S,andSi+1S0,SnisobtainedfromSibycuttingalongacircleCiandcappingthehole(s).
CiOurtaskwillbetoensurethatCiisnon-separatinginSiforeveryi=0,n1.
ThenLemmaB.
4willimplythatε(Si+1)ε(Si)1foralliandε(Si+1)ε(Si)2wheneverCi∈C12,givingε(S)ε(Sn)+|C1|+|C22|+2|C12|/2|C|asdesired.
C9C1C2D0C3C4C5C6C7C8C9Fig.
B.
1.
Cuttingthe1-sidedcircleC1andthe2-sidedcirclesC2,C3andC5,C7,C8andC9doesnotseparateSCuttingalongthecirclesinC1(andcappingtheholes)isstraightfor-ward:sincethesecirclesareone-sided,theyarealwaysnon-separating.
Next,weconsiderthecirclesinC22,suchasC9inFigureB.
1.
ForeveryC∈C22,denotebyD(C)thecomponentofSCthatdoesnotcontainD0.
SinceeverycircleinCliesintheclosureofD0butnoSurfaces405pointofD(C)does,theseD(C)arealsocomponentsofSC.
Inparticular,theyaredisjointfordierentC.
Thus,eachD(C)willalsobeacomponentofSiC,whereSiisthecurrentsurfaceafteranysurgeryperformedonthecirclesinC1andinsideD(C)forsomeC=C.
GivenaxedcircleC∈C22,letSbethesurfaceobtainedfromD(C)bycappingitshole.
SinceCdoesnotboundadiscinSthatisdisjointfromD0,weknowthatSisnotasphereandhencecontainsanon-separatingcircleC(LemmaB.
1).
WechooseCsothatitavoidsthecapweaddedtoformS,i.
e.
sothatCSC.
ThenCisalsonon-separatinginthecurrentsurfaceSi(sinceeverypointofSiCcanbejoinedbyanarcinSiCtoC,whichisconnected),andwemayselectCasacircleCitocutalong.
ItremainstoselectatleasthalfofthecirclesinC12ascirclesCitocutalong.
Webeginbyselectingallthosewhoseentirestripneighbourhoods(i.
e.
,boththeir'sides')lieinD0.
(InFigureB.
1,thesearethecirclesC2andC3.
)ThesecirclesCarenon-separatingalsointhesurfaceSicurrentbeforetheyarecut,becauseD0willlieinsideacomponentofSiC.
EveryotherC∈C12liesintheclosurealsoofacomponentD(C)=D0ofSC.
(InFigureB.
1,thesearethecirclesC4,C8.
)ForeverycomponentDofSCweselectallbutoneofthecirclesC∈C12withD(C)=DasacuttingcircleCi.
Clearly,eachoftheseCiwillbenon-separatingalsoinitscurrentsurfaceSi,andtheirtotalnumberatleast|C12|/2.
HintsforalltheExercisesAtthispointinthebookthereusedtobeacollectionofhintsforalltheexercises.
Theirintentionwastohelpthosewhohadalreadyspentsometimeoveranexercisebutsomehowfailedtomakeprogress,byputtingthemontherighttrack.
Inordertonotspoilthefunofanexercise,oritsusabilityinclass,Itriedtodesignthesehintssoastomakethemsomewhatunintelligibletothosethathadnotmadesuchaninitialattemptoftheirown.
However,thisisatrickybrief,andinsomecasesthehintswillinvariablystillgiveawaysomekeyideas,ornarrowastudent'smindinpursuitofalternatives.
Itthereforeseemedbesttoleavethedecisionofwhichhintstoincludetothelecturersettingtheproblems.
TheHintssectionstillexists,andisregularlyupdated.
Asofthisftheditionofthebook,however,IhaverelegatedittotheProfessionaleBookedition.
Thisisavailabletolecturersandprofessionalmathemati-ciansviahttp://diestel-graph-theory.
com/and,foriPadusers,fromthebook'sdedicatediOSapp,GraphTheory.
(Thisgivescontinuedaccesstoearliereditionstoo,whichcontainsomeproofsnolongerincludedinlatereditions.
)Iapologizetothosereadersthatareusingthebookforself-studyandwouldhavelikedapeekatahinteverynowandthentoo.
.
.
.
R.
Diestel,GraphTheory,GraduateTextsinMathematics173,DOI10.
1007/978-3-662-53622-3ReinhardDiestel2017407IndexPagenumbersinitalicsrefertodenitions;inthecaseofauthornames,theyrefertotheoremsduetothatauthor.
Thealphabeticalorderignoreslettersthatstandasvariables;forexample,'k-chromatic'islistedundertheletterc.
above,15abstractdual,112–113,116graph,3,89,92,98,332acyclic,13–14,49,144adhesion,352,373adjacencymatrix,27adjacent,3Aharoni,R.
,57,232,238,240,241,275,276,277,278Ahuja,R.
K.
,171algebraiccolouringtheory,147owtheory,154–169,171graphtheory,23–27,34planaritycriteria,107–109algorithmicgraphtheory,171,381,390–391almost,332,342,343Alon,N.
,10,34,130,147,344alternatingpath,36,239–240walk,68ambientgraph,354Andreae,Th.
,222,275,276antichain,53,56,266,348antihole,137apexvertices,372,387Appel,K.
,146–147arboricity,48–51,123,202,252andcolouringnumber,143arc,90,249,270,278–279,280,281,399-component,249-connected,249,269jumping,248Archdeacon,D.
,390Arnborg,S.
,390articulationpoint,seecutvertexAsratian,A.
S.
,309at,2augmentingpathformatching,36,53,240,267fornetworkow,153,169automorphism,3,31,230,264averagedegree,5bounded,305andchoicenumber,130andchromaticnumber,125,130,180,183,202andconnectivity,12forcingminors,173,180–182,202,204–207forcingtopologicalminors,180–182andgirth,8,9–10,331andlistcolouring,130andminimumdegree,5–6andnumberofedges,5andRamseynumbers,305andregularitylemma,187–188,204R.
Diestel,GraphTheory,GraduateTextsinMathematics173,DOI10.
1007/978-3-662-53622-3ReinhardDiestel2017409410Indexavoid,361Babson,E.
,148back-and-forthtechnique,229,230badsequence,348,388balanced,56,341Bauer,321Behzad,M.
,148Bellenbaum,P.
,389below,15Berge,C.
,137Berger,E.
,232,279Bernstein,238between,6,90Biggs,N.
L.
,34binarytree,218,267bipartitegraphs,17–18,32,115,119,135edgecolouringof,127,144,145ownumberofcubic,160forcedassubgraph,179,195list-chromaticindexof,132–134,148matchingin,35–41,238–240inRamseytheory,295–296,304Birkho,G.
D.
,147block,60,142k-block,354graph,61,83B¨ohme,T.
,86,205Bollobas,B.
,85,86,204,205,206,275,305,321,334,336,341,344,391bond,24,32,60,111–113,118-cycleduality,25,111–113,162–164space,seecutspaceBondy,J.
A.
,321boundarycircle,399ofaface,92–94,115,116,401map,34,116ofawave,233boundedsubsetofR2,92,399boundedgraphconjecture,274χ-bounded,142Bowler,N.
,48,50,57,274,275bramble,355–359,385,386,388,389number,359orderof,355branchdecomposition(rephrased),359set,19intree-decomposition,359vertex,19Brandt,S.
,204bridge,11,43,151,161,165–167Broersma,321Brooks,R.
L.
,123,143theorem,123,147listcolouringversion,148Bruhn,H.
,118,274,275,277,279,280,311,321Burr,S.
A.
,305Cameron,P.
J.
,276Cantor,238set,268capacity,152function,151cardinality,393Carmesin,J.
,48,50,57,274,275,388,390Catlin,P.
A.
,206Cayley,A.
,147,343centralfaceingrid,375vertex,9,375centre,18certicate,135,374,391chain,15,53,58,266,394,396exchangechain,50Chebyshevinequality,337Cherlin,G.
,276choicenumber,130,144,145andaveragedegree,130ofbipartiteplanargraphs,145ofplanargraphs,130,144k-choosable,130chordofcycle,8ofspanningtree,14chordal,135–136,145,353,384k-chromatic,119,143chromaticindex,120,127ofbipartitegraphs,127vs.
list-chromaticindex,130,132andmaximumdegree,129–130chromaticnumber,119,143,164,215,273,387andKr-subgraphs,125,135,241ofalmostallgraphs,334andaveragedegree,125–126,130,180,183,202vs.
choicenumber,130andcolouringnumber,123andconnectivity,125,147constructions,126–127,144,147inextremalgraphtheory,179andownumber,164Index411forcingminors,183–187,202,203,206–207forcingshortcycles,124,331forcingsubgraphs,125,262,303forcingatriangle,144,303andgirth,125,147,187,331asaglobalphenomenon,125,135andmaximumdegree,123andminimumdegree,123,125andnumberofedges,122chromaticpolynomial,143,172Chudnovsky,M.
,137,142,148,305Chung,F.
R.
K,34Chvatal,V.
,288,309,310,312,321circleboundarycircle,399ingraphwithends,113,250,399Hamilton,311,319,321,322one/two-sided,400insurface,381,399,400,403unitcircleS1,399circuit,24,250,269–272circulation,150–151,163,170circumference,8,385andconnectivity,308andminimumdegree,8class1vs.
class2,129classicationofsurfaces,399–400cliquenumber,135–142,295closedunderaddition,154,254underinnitesums,254underisomorphism,3,332,369wrt.
minors,145,170,275,369,374,382,385wrt.
subgraphs,135,145wrt.
supergraphs,135,336upordown,intree-order,15walk,10closure(ofaset),246coboundarymap,34k-colourable,119,129–130,215,353colourclass,119colour-critical,seecriticallyk-chromaticcolouring,119–148,184,215algorithms,122,143andows,162–165number,122,143,145,247,274planegraphs,120–121,162–165inRamseytheory,285total,145,1483-colourtheorem,seethreecolourthm.
4-colourtheorem,seefourcolourthm.
5-colourtheorem,seevecolourthm.
comb,210,268modied,265star-comblemma,219combinatorialisomorphism,99,99,116settheory,273,305Comfort,W.
W.
,273compact,215,246,268compactnessprinciple,397,216,274prooftechnique,214–216,252–261,263,274fortree-width,387comparabilitygraph,135,145,146complementofabipartitegraph,135,145ofagraph,4andperfection,137–138ofaproperty,369,374–375completebipartitegraph,17graph,3,160innitegraph,211,373matching,see1-factorminor,103,107,180–187,202,203,205–207,373,380–382multipartitegraph,17,177partofpath-decomposition,385partoftree-decomposition,353r-partitegraph,17separator,353,384subgraph,125,135–136,173–177,353topologicalminor,75,86,103,107,117,180–182,184,185,187,202,207complexitytheory,135,382,391component,11,399arc-,249connected,10arc-connected,249,269,2782-connectedgraphs,59–61,83,95,100,302,3143-connectedgraphs,62–66,83,95,103–104,109,301,3024-connectedgraphs,116,301,302,311k-connected,11,12–13,72,83externally,359innitelyconnected,211,262,274locally,269minimallyconnected,14minimallyk-connected,85strongly(indigraphs),32topologically,249412Indextree-decomposition,360tree-width,360,384,385andvertexenumeration,10,14connectedness,10,14connectivity,12,10–13,59–86andaveragedegree,12andchromaticnumber,124–125,147andedge-connectivity,12inambientgraph,343,373andgirth,262,331andHamiltoncycles,310–311,320,321,322ininnitegraphs,239–241forcingminors,387andlinkability,75–76,85,87andminimumdegree,13,279andplaneduality,116andplanerepresentation,102andRamseyproperties,300–302ofarandomgraph,333viaspanningtrees,48,58consistentorientedseparations,361k-constructible,126–127,144,147–148contains,3continuum,269continuummany,393contraction,19–22and3-connectedness,62–65map,19,31minor,19inmultigraphs,28–30,170andtree-width,353convexdrawing,105,114,117polygon,303Corneil,D.
G.
,390Cornuejols,G.
,148countablegraph,2set,393countablyinnite,393coverbyantichains,55–56ofabramble,355bychains,53bycycles,115,170double,115byedges,145bypaths,52–54,238bytrees,48–51,113,117,278byvertices,35,36,45–47,355,370criticalk-chromatic,123,143factor-,43,240,263crosscap,400,402cross-edges,24,48,252crossesingrid,356crown,301–302cubed-dimensional,30,343ofagraph,G3,320cubicgraph,51-factorin,43,55ownumberof,160,161,167,171,172multigraph,46,55,167cu,372Curran,S.
,58cut,24capacityof,152,153-cycleduality,25,111–113,162–164-edge,seebridgeeven/odd,254,272,280owacross,151fundamental,26,32,254,271minimal,24,60,111innetwork,152space,25–28,32,107,112,271,280cutvertex,11,60cycle,8-bondduality,26,111–113,162–164directed,144,145disjointcycles,45–47doublecover,115,166,170edge-disjointcycles,202,262,303expectednumber,328facial,107fundamental,26,32geodesic,32,360Hamilton,170,307–322innite,311,319induced,8,65–66,95,109,136,136,271innite,113,250,279,311length,8long,8,30,84,143inmultigraphs,29non-separating,65,95,109,271odd,18,123,137withorientation,162–164short,10,124,182–183,329–331space,24–28,32,65–66,107–109,112,115,254–257,271,279,280topological,254–257,279,280thresholdfunction,341,342,343cyclomaticnumber,24cylinder,400Index413Czipszer,J.
,279Dean,N.
,321deBruijn,N.
G.
,215,274decomposition,see:edge-decomposition.
.
.
tree-decomposition.
.
.
packing.
.
.
degeneracy,seecolouringnumberdegree,5ofanend,218,247,247,279ataloop,29sequence,311deletion,4Δ-system,303densegraphs,174,177,178linearorder,265densityedgedensity,174ofpairofvertexsets,187upperdensity,201depth-rstsearchtree,16,31Deuber,W.
,291,305diameter,8–9,342andgirth,9andradius,9Diestel,R.
,118,205,206,231,244,247,252,255,256,259,273–280,354,367,373,374,388–391dierenceofgraphs,4,92digon,seedoubleedgedigraph,seedirectedgraphDilworth,R.
P.
,53,56,266Dirac,G.
A.
,206,308directedcycle,144,145edge,28graph,28,52,133,144,276path,52,143direction,150disc,399disconnected,10disjointgraphs,3dispersed,264distance,8dominateanend,263,264doublecounting,117,139–140,327,338cover,115,170edge,29,110ray,210,265,280,321wheel,301down(-closureetc.
),15drawing,2,89,98convex,105,117straight-line,105,114dualabstract,112–113,116,117andconnectivity,116plane,110–111,116,117dualitycyclesandbonds,26–28,111–113,156owsandcolourings,162–165forinnitegraphs,113,117,118ofplanemultigraphs,110–113tree-decompositionsandbrambles,356,359duplicatingavertex,137edge,2crossingapartition,24deletion,62directed,28double,29ofamultigraph,28plane,90topological,245X–Yedge,2edge-chromaticnumber,seechromaticindexedgecolouring,120,127–129,285,291andownumber,160andmatchings,144-edge-connected,12edge-connectivity,12,48,72,143,160,211edgecontraction,19and3-connectedness,62vs.
minors,19inmultigraph,29edgecover,49,145edge-decomposition,49intocircuits,24,254,280intoconnectedsubgraphs,49intoforests,50edgedensity,5,6,174andaveragedegree,5forcingminors,182forcingpathlinkages,76–82forcingsubgraphs,174–179forcingtopologicalminors,181andregularitylemma,187–188,204,207edge-disjointspanningtrees,48–52,55,211edge-end,264,273414Indexedge-maximal,4vs.
extremal,175,185withoutIK5,185,186withoutTK3,3,203withoutTK4,184–185withoutTK5,TK3,3,106edgespace,23,32,107,254Edmonds,J.
,57,240,391embeddingofbipartitegraphs,296–297ofgraphs,21k-nearembedding,372intheplane,98,100–118inS2,91–92,98self-embedding,381insurface,97,117,372–382,387,391,401emptygraph,2,11enddegree,218,247,264,278–279insubspaces,247,247,278–279ofedge,2,28-faithfulspanningtree,268ofgraph,52,113,209,217–218,219–227,245–273,278–279ofpath,6space,268thick/thin,223–227,264oftopologicalspace,269endpointsofarc,90,247endvertex,2,6terminalvertex,28enumeration,393equivalenceindenitionofanend,217,269ofgraphinvariants,202ofgraphproperties,302ofplanarembeddings,98–102,113,114ofpointsintopologicalspace,90,399inquasi-order,382Erdos,P.
,47,57,125,147,178,179,197,204,206,207,215,228,231,232,273,274,275,276,279,291,303,305,309,321,323–324,326,329–331,335,341,344Erdos-Hajnalconjecture,148,285,305Erdos-Mengerconjecture,232,276–277Erdos-Posaproperty,46,55,370–371,386,387Erdos-Posatheorem,47,57edgeversion,202,303generalization,370–371inniteversion,264Erdos-Sosconjecture,179,202,204Erdos-Stonetheorem,174,178–179,197–198,204Euler,L.
,22,33,97characteristic,401formula,97–98,114,401genus,376,401–403tour,22,272Euleriangraph,22innite,272,279evendegree,22,24,41graph,160,161,170,279event,325evolutionofrandomgraphs,342,344exactsequence,115exceptionalset,188exchangechain,50excludedminors,seeforbiddenminorsexistenceproof,probabilistic,147,323,329,329–331expandingavertex,137expectation,327–329,336exteriorface,seeouterfaceexternalconnectivity,359extremalbipartitegraph,201vs.
edge-maximal,174–175,185graphtheory,180–207,279graph,174–177withoutIK5,185,186withoutTK3,3,203withoutTK4,184–185face,90,401centralface,375ofhexagonalgrid,375facialcycle,107factor,351-factor,33–45,55,239–241,263,2671-factortheorem,42,43,55,57,85,86,240,2772-factor,42k-factor,35factor-critical,43,240,263Fajtlowicz,S.
,206fan,71,263-versionofMenger'stheorem,71,263niteadhesion,373graph,2set,393tree-width,373niteintersectionproperty,216Index415nitelyseparable,264rstordersentence,333,344rstpointonfrontier,90shlemma,367vecolourtheorem,120,148,167listversion,130–131,148ve-owconjecture,166,167,171–172Fleischner,H.
,314,319,320,321ow,149–172,151–1522-ow,1593-ow,160,167,1704-ow,160–161,166–167,163,171,1726-owtheorem,167–169,171,172k-ow,157–161,165–169,170,171,172H-ow,154–159,169-colouringduality,162–165conjectures,166–167,171,172group-valued,154–159,171–172integral,152,154networkow,151–154,169,171number,157–161,165,170inplanegraphs,162–165polynomial,156,159,171totalvalueof,152football,114forbiddenminorsandchromaticnumber,183–187expressedby,369,374–382ininnitegraphs,231,273,274,373–374minimalsetof,373,374,385,390planar,342andtree-width,355–373forciblyhamiltonian,seehamiltoniansequenceforcingIKr,180–187,205–206,373,387IK0,373–374,387TK5,186,206TKr,75,181–182,184,187,205–206edge-disjointspanningtrees,48Hamiltoncycles,308–311,314,319,320,321,322highconnectivity,12inducedtrees,179largechromaticnumber,126–127linkability,75–77,87longcycles,8,30,84,143,307–322longpaths,8,30minorwithlargeminimumdegree,182,205shortcycles,10,182–183,187,331subgraph,15,173–179,187–207tree,15,179triangle,144,303Ford,L.
R.
Jr.
,153,171forest,13,184,369minor,390partitions,51–52,57,264plane,94,113topological,264tree-widthof,369,384fourcolourproblem,147,206fourcolourtheorem,120,166,171,183–184,185,203,311,320history,147four-owconjecture,166–166Fra¨sse,R.
,276Frank,A.
,85,171Freudenthal,H.
,277compactication,246,277ends,269from.
.
.
to,6frontier,90,399Fulkerson,D.
R.
,153,171fullerene,113–114fundamentalcircuit,254,254,271cut,26,32,254,271Gale,D.
,38Gallai,T.
,33,45,52,56,57,58,86,204,263,279Gallai-Edmondsmatchingtheorem,43–45,57,238,277Galvin,F.
,134,148Gasparian,G.
S.
,137,148Geelen,J.
,391generated,254genusEulergenus,376,401–403ofagraph,387orientable,387ofasurface,381geodesic,360cycle,32,360geometricdual,seeplanedualGeorgakopoulos,A.
,278,279–280,319Gibbons,A.
,171Gilmore,P.
C.
,146girth,8andaveragedegree,8–9,331andchromaticnumber,125,147,329–331andconnectivity,87,262,331anddiameter,9416Indexandminimumdegree,8,10,30,182,331andminors,182–183,203,205andplanarity,262andtopologicalminors,183,187Godsil,C.
,34Golumbic,M.
C.
,148goodcharacterization,374,391pair,348,380sequence,348Gorbunov,K.
Yu.
,390G¨odel'scompactnesstheorem,274G¨oring,F.
,86Graham,R.
L.
,304graph,2–4,27–28,30homogeneous,230,265,276invariant,3,30,202,327minortheorem,347,380–381,374,388,389,390fortrees,349–350partition,52plane,90–98,110–113,120–121,131–132,162–165process,345property,3,228,302,332,342,343,369,374,391simple,30universal,228–231,228,265,276graphicsequence,seedegreesequencegraph-theoreticalisomorphism,99greedyalgorithm,122,133,142,143grid,114,223,356canonicalsubgrid,376hexagonalgrid,223,224,375–380minor,265,359,370,387theorem,370tree-widthof,359,384,388Grohe,M,373,391Gr¨otzsch,H.
,121,147,167,171group-valuedow,154–159,171–172Gr¨unwald,T.
,seeGallaiGuseld,D.
,57Guthrie,F.
,146Gyarfas,A.
,148,179,207Hadwiger,H.
,184,205,206conjecture,183–187,203,205,206inniteanalogue,262,274Hajnal,A.
,273,274,275,279,291,304,305Hajos,G.
,126,147,187conjecture,187,205construction,126–127Haken,W.
,146–147Halin,R.
,85,86,221,223,273,274,275,278,388,391Hall,P.
,38,54,56,238Hamilton,W.
R.
,320Hamiltoncircle,311,319,321,322Hamiltoncycle,307–322inG2,314–319inG3,320inalmostallgraphs,342anddegreesequence,311–313,320andthefourcolourtheorem,311and4-ows,170,311ininnitegraph,seeHamiltoncircleinlinegraphs,322andminimumdegree,308inplanargraphs,311powerof,319sucientconditions,307–313Hamiltonpath,307,313,319,320hamiltoniangraph,307sequence,312handle,400,402Harant,J.
,86head,seeterminalvertexHeawood,P.
J.
,147,170Heesch,H.
,147height,15hexagonalgrid,223,224,375–380Higman,D.
G.
,348,388Homan,A.
J.
,146hole,137Holz,M.
,277homogeneousgraphs,230,265,276homomorphism,3,145Hoory,S.
,10,34Huck,A.
,274hypergraph,28incidence,2encodingofplanarembedding,seecombinatorialisomorphismmap,29matrix,27,33,34poset,109incident,2,92incomparabilitygraph,267increasingproperty,336,343independencenumber,135–142andconnectivity,308–309andcovers,52,55andHamiltoncycles,308–309andlongcycles,143Index417andperfection,140ofrandomgraph,326,342independentedges,3,33–45,55events,325paths,7,71–73vertices,3,52,133,326indicatorrandomvariable,328inducedsubgraph,3–4,72,135–136,136,140ofalmostallgraphs,332,343cycle,8,32,65,66,95,109,136,13,279ofallimperfectgraphs,137,145ofalllargeconnectedgraphs,300inRamseytheory,284,290–300,303inrandomgraph,326,343tree,179,202inductiontransnite,213–214,395Zorn'sLemma,212,262,396inductiveordering,213innitegraphs,2,20,32,54,118,201,209–281,284,311,319,321,322,334,335373–374,381,388,390,391sequenceofsteps,211,221set,393basicproperties,211–212innitelyconnected,211,262innitylemma,215,274generalized,215,274,396initialsegment,394vertex,28innerface,90point,245vertex,6,13integralow,152,154function,152interiorofanarc,90ofapath,P,6–7internallydisjoint,seeindependentintersection,3graph,384intervalgraph,135,145,385into(fortree-decompositions),351invariant,3irreduciblegraph,384Irving,R.
W.
,57isolatedvertex,5,343isomorphic,3isomorphism,3ofplanegraphs,98–102isthmus,seebridgeItai,A.
,58Jaeger,F.
,171Janson,S.
,344Jensen,T.
R.
,146,172,390Johnson,D.
,373join,2Jonsson,B.
,276Jordan,C.
,90,92Jordancurvetheorem,90,117jumpingarclemma,248Jung,H.
A.
,75,206,220,264,275Khachatrian,N.
K.
,309Kahn,J.
,148Karonski,M.
,344Kawarabayashi,K.
,205,390Kelmans,A.
K.
,109,118Kempe,A.
B.
,147,321kernelofdirectedgraph,133,145ofincidencematrix,27Kirchho'slaw,149,150Kleitman,D.
J.
,147knotlessgraph,382knottheory,172Kochol,M.
,159,171Kollar,J.
,204Komlos,J.
,204,205,207,305,319,322K¨onig,D.
,35,56,127,215,274dualitytheorem,35,52,54,56,68,135,145,239innitylemma,215,274K¨onigsbergbridges,22Korman,V.
,241Kostochka,A.
V.
,182,205,305Kozlov,D.
,148Kriesell,M.
,56Krivelevich,M.
,207Kruskal,J.
B.
,349,388K¨uhn,D.
,87,183,187,205,206–207,231,276–280Kuratowski,C.
,102–107,117,263,390-theoremforhighersurfaces,375-typecharacterization,114,125,302,374,390–391Kuratowskisetofgraphs,374,390ofgraphproperties,302418IndexLachlan,A.
H.
,230,276Laplacian,34largewave,233Larman,D.
G.
,75Latinsquare,144Laviolette,F.
,280Leader,I.
B.
,274,275leaf,13,15,30,219leantree-decomposition,359Lee,O.
,58lengthofacycle,8ofapath,6,8ofawalk,10level,15liftinganedge,315limit,214–215,394wave,234line(edge),2graph,4,120,145,203,322segment,90linearalgebra,23–28,107–109,141decomposition,372programming,171Linial,N.
,10,34linkable,234linkedbyanarc,90byapath,6k-linked,74–82,85,87,181vs.
k-connected,74–76,85,87tree-decomposition,359vertices,6,90list-chromaticindex,130,132–134,144,148-chromaticnumber,seechoicenum-bercolouring,130–134,148bipartitegraphs,132–134,145Brooks'stheorem,148conjecture,132,145,148k-list-colourable,seek-choosableLiu,X.
,148Lloyd,E.
K.
,34locallynite,210,273–281locallyconnected,269logarithms,1loop,28Lovasz,L.
,56,137–138,140,147,148,204Luczak,T.
,344,345MacLane,S.
,107,117,118Mader,W.
,12,33,72,86,87,182,205,206,388Magnanti,T.
L.
,171Maharry,J.
,205Mani,P.
,75mapcolouring,119–121,142,143,146–147,162Markovchain,345Markov'sinequality,329,329,336marriagetheorem,37–38,40,54,56–57,238–239,263stable,40,56–57,134Marx,D.
,373matchable,43,239matching,35–57inbipartitegraphs,34–41,135andedgecolouring,144ingeneralgraphs,39–45ininnitegraphs,239–241,267,277partial,239,267stable,40,55,134ofvertexset,35Mate,A.
,273,305matroid,57,58,118,391innite,274,280max-owmin-cuttheorem,151,153,169,171maximal,4acyclicgraph,14element,394,396planargraph,102,107,114,115,117,186,203planegraph,94,102wave,234maximumdegree,5bounded,196–197,288andchromaticnumber,123andchromaticindex,127–130andlist-chromaticindex,134,148andradius,9andRamseynumbers,288–289andtotalchromaticnumber,145Mazoit,F.
,389Menger,K.
,56,66–71,84,86,169,221,239–241,266,276–277theoremof,66–71,84,86,169,221–222,231,232,263,276–277metrizable,247,269Milgram,A.
N.
,52,56,58Milner,E.
C.
,275minimal,4connectedgraph,14k-connectedgraph,85Index419cut,24,60,111,156element,394non-planargraph,114separator,82–83setofforbiddenminors,374,385,390minimumdegree,5andaveragedegree,5andchoicenumber,130–131andchromaticnumber,123,125andcircumference,8andconnectivity,13,86,279andedge-connectivity,12forcingHamiltoncycle,308,319forcinglongcycles,8forcinglongpaths,8,30forcingshortcycles,10,182–183,187,331forcingtrees,15andgirth,8,9,10,182–183,205,331andlinkability,76minor,19–22,19,180–183K3,3,117,203K4,184–185,369–370K5,185,186,206,384K5andK3,3,102–107K6,186Kr,181,182,183,184,202,203,205–207,343,373,387K0,373–374,387ofalllarge3-or4-connectedgraphs,301–302-closedgraphproperty,369,374–382,385contraction,20excluded,seeforbiddenforbidden,183–187,231,274,369–382,385,388–391forced,182,184,180–187incomplete,205innite,211,222–223,231,264,275,276,277,279,387,390model,19ofmultigraph,29Petersengraph,166andplanarity,102–107,114proper,381relation,20,32,222,231,265,276,302,355,374theorem,347,374–382,374,390–391proof,374–381fortrees,349–350vs.
topologicalminor,20–22,103andWQO,347–391(seealsotopologicalminor)M¨obiuscrown,301–302ladder,186strip,400modelofaminor,19Mohar,B.
,117,147,205,391momentrst,seeMarkov'sinequalitysecond,335–342monochromatic(inRamseytheory)inducedsubgraph,289–300(vertex)set,286–287subgraph,285,287–289Moorebound,10,34M¨uller,Th.
,389multigraph,28–30cubic,46,55,166listchromaticindexof,148plane,110multipleedge,28Murty,U.
S.
R.
,321Myers,J.
S.
,205Nash-Williams,C.
St.
J.
A.
,48,51,57,252,273,276,278,280,321,388k-nearembedding,372nearlyplanar,373Negami,S.
,86Negropontis,S.
,273neighbourofasetofvertices,5ofavertex,3Neˇsetˇril,J.
,304,305nestedseparations,367,384network,151–154theory,171Niedermeyer,F.
,274,277node(vertex),2normaltree,15–17,31,165,170,303ininnitegraphs,220,247,254,264,269,278,374,391ray220,264nowheredense,49zero,154,171null,seeemptyobstructiontosmalltree-width,355–359,367octahedron,12,17,390oddcomponent,41,263420Indexcycle,18,123,137,144,145,148degree,5,320on,2one-factortheorem,42,57,86,240openEulertour,272Oporowski,B.
,301,305,388orderofabramble,355ofagraph,2partial,15,20,31,32,52–54,56,145,382,393,394,396quasi-,348ofaseparation,11,360tree-,15,31type,394well-quasi-,347–349,374,382,383,388ordinal,394–395orientablesurface,387planeas,157orientationacyclic,143ofacycle,162–163ofaedge,150ofagraph,28,133,143,171,202ofaseparation,361Orlin,J.
B.
,171orthogonalsubspaces,25Osthus,D.
,87,183,187,205,206–207outerface,90,99–100,115outerplanar,115,385over,362Oxley,J.
G.
,118,278,301,305Oxtoby,J.
C.
,273packing,35,45–52,252,263-coveringtheorem,49,263,272tree-,49Palmer,E.
M.
,344paralleledges,29parity,5,41,44partoftree-decomposition,351partiallyorderedset,52–54,56,269,394,396r-partite,17partition,1,51,285edge,49pass,315pasting,136,184,185,203,353,384path,6–10,210a–b-path,7,71A–B-path,7,63–71,84,231–238,262H-path,7,63,72–73,84alternating,36–37,38,68betweengivenpairsofvertices,74–82-connected,278cover,52–54,52,238-decomposition,372,385directed,52,143disjointpaths,52,62–71,74–82,231–237edge-disjoint,48,71,73-hamiltoniansequence,313independentpaths,7,71,72–73,84,85induced,302length,6linkage,74–82,87long,8-width,385,390perfect,135–142,145,148,241graphconjectures,137graphtheorems,137,137,145,148matching,see1-factorstrongly,241,267weakly,241,267Petersen,J.
,43Petersengraph,166piecewiselinear,89planar,102–117,120–121,131,231,370,371,373embedding,98,102–117nearlyplanar,373planaritycriteriaKelmans,109Kuratowski,107MacLane,107Tutte,117–118Whitney,113planedual,110duality,110–113,135,117,156–165graph,90–98multigraph,110–113,116,117,156–165triangulation,96,97,170,353Platonicsolid,113–114Plummer,M.
D.
,56Podewski,K.
P.
,277point(vertex),2pointwisegreater,312Polat,N.
,278polygon,90polygonalarc,90,91Posa,L.
,47,57,291,305powerofagraph,314,320set,393Index421predecessor,394preferences,40,54,134Prikry,K.
,275probabilisticmethod,323,329–331,344projectiveplane,390properminor,381separation,11subgraph,3wave,233property,3,302,332ofalmostallgraphs,332–335,341–342equivalence,302increasing,336minor-closed,369,385non-trivial,302Proskurowski,A.
,390pruning,242pseudo-randomgraph,304Pym,J.
S.
,238,277quasi-ordering,347–349,374,382,383,388radius,9anddiameter,9,30andmaximumdegree,9Rado,R.
,56,273,276,305graph,229–230,265,276,334,335Rado'sselectionlemma,274Ramsey,F.
P.
,284–287Ramseygraph,290-minimal,296–297numbers,285,287,303,305,326,344Ramseytheory,267–305andconnectivity,300–302induced,297–300innite,286,303,304randomgraph,175,187,287,344–345,325evolution,342,344innite,334process,345uniformmodel,344,345randomvariable,327indicatorr.
v.
,328rank,243ray,210,215,219,221,261,264,265,269,374double,210,265,275,280,321normal220,264spanning,321rayless,214,243ranking,243recursivedenitions,242–244pruningoftrees,242reducibleconguration,147Reed,B.
A.
,57,388reningapartition,1,190–193region,90–92onS2,92regular,5,39,41,144,319-regularpair,187,203forsparsegraphs,207partition,188regularitygraph,196inated,Rs,288lemma,174,187–200,188,204,304forsparsegraphs,207Reiher,C.
,204,274Renyi,A.
,228,276,335,341,344Richardson,M.
,145Richter,B.
,391rigid-circuit,seechordalring,375,376Robertson,N.
,57,137,147,148,172,186,206,355,370,372,374,388–390,391R¨odl,V.
,288,291,305Ronyai,L.
,204root,15rootedtree,15,349,383Rothschild,B.
L.
,304Royle,G.
F.
,34Rucinski,A.
,344Salazar,G.
,391Sanders,D.
P.
,147Sark¨ozy,G.
N.
,319,322saturated,seeedge-maximalSauer,N.
,276Schnyder,W.
,109Schoenies,A.
M.
,90Schrijver,A.
,56,57,85,86,148,171Schmidt,R.
,277Schur,I.
,303Scott,A.
D.
,142,207,276secondmoment,335–342,337self-minorconjecture,381,387,388separateagraph,11,67,72theplane,90422Indexseparatingcircle,400,403separation,11corner,363crossing,363nested,384orderof,11oriented,361inducedbyatree-decompositions,352,361,367,384,386starof,361submodularity,363separator,11sequentialcolouring,seegreedyalgo-rithmseries-parallel,203setk-set,1countable,393countablyinnite,393nite,393innite,393powerset,393system,seehypergraphwell-founded,394Seymour,P.
D.
,57,86,137,142,147,148,148,167,172,186,206,319,322,355,355,370,371,372,374,381,388,389,390,391Shapley,L.
S.
,38Shelah,S.
,274,275,276,277Shi,N.
,276sideofacut,24Simonovits,M.
,57,204,207,305simple,30simplicialtree-decomposition,259,353,384,388six-owtheorem,167,172smallwave,233snark,166planar,166,171,311Sos,V.
,179,202,204spannedsubgraph,4spanningray,321astandardsubspace,247subgraph,4trees,14,16edge-disjoint,48–52end-faithful,268normal,15–17,31,220,247,254,264,268,275,374,391numberof,343topological,instandardsubspaces,271topological,52,250–257,269,271,280sparsebasis,107graph,173,180–183,203,207,288,305regularitylemma,207Spencer,J.
H.
,304,344Sperner,E.
,54sphereS2,92,99–100,399spine,210splittertheorem,86splittingavertex,65Spr¨ussel,Ph.
,279squareofagraph,314–319,320,321Latin,144stabilitynumber,seeindependencenumberstablemarriage,40,57,134matching,40,55,134set,3standardbasis,23subspace,246,247,249,250,253,246,269topologicalspanningtreesin,270,271star,18,202,290,302centreof,18induced,300innite,219ofseparations,361star-comblemma,219,220Steens,K.
,240,277Stein,M.
,277,279Steinitz,E.
,117stereographicprojection,92Stillwell,J.
,117Stone,A.
H.
,178,195straightlinesegment,90stripneighbourhood,94,400strong-lyconnected,32-lyperfect,241,267subcontraction,seeminorsubdividingvertex,19subdivision,19submodularityoforderofseparations,363subgraph,4ofalllargek-connectedgraphs,300–302Index423forcedbyedgedensity,174–179,187–201,202,203ofhighconnectivity,12induced,4oflargeminimumdegree,6,123,145spanning,4successor,394Sudakov,B.
,207,305sumofedgesets,23ofows,159ofthinfamilies,254supergraph,4suppressingavertex,29,46–47,64–65surface,372,375,376,399–405surgeryon402surgeryonsurfaces402capping402cutting402symmetricdierence,23,36,69systemofdistinctrepresentatives,54Szabo,T.
,204Szekeres,G.
,303Szemeredi,E.
,187,205,207288,305,319,322seealsoregularitylemmatailofanedge,seeinitialvertexofaray,210,261Tait,P.
G.
,147,321tangle,362,389–390dualitytheorem,362Tarsi,M.
,147teeth,210terminalvertex,28thick/thinend,223–227,264thinend223–227,251family,254sum,254Thomas,R.
,57,76,86,137,147,148,172,186,206,301,305,321,356,360,388–391Thomason,A.
G.
,205,336Thomasse,S.
,276Thomassen,C.
,117,131,147,148,183,205,206,277,278,321,322,390,391,403threecolourtheorem,121three-owconjecture,167thresholdfunction,335–342,343,344Toft,B.
,147,172topologicalconnectedness,247,253cyclespace,254–257,279,280edge,245enddegree,247space|G|,245–261,269Eulertour,272isomorphism,99,99,111spanningtree,52,250–257,269,271,280topologicalminor,19K3,3,98,103,106,107,117,203K4,64,184–185,203,369–370K5,98,103,106,107,117,186,206,384K5andK3,3,98,103,106,107,115,117Kr,75,175,181–183,187,202,203,207,284,300,360,373K0,211,220,264,266,374,387ofalllarge2-connectedgraphs,301forcedbyaveragedegree,181–183forcedbychromaticnumber,187forcedbygirth,183,187induced,181asorderrelation,20vs.
ordinaryminor,20,103andplanarity,98,102–107tree(induced),179andWQOofgeneralgraphs,383andWQOoftrees,349torso,352,372–373totalchromaticnumber,145totalcolouring,145conjecture,145,148totalvalueofaow,152touchingsets,355t-tough,310–311,319,320toughnessconjecture,310,319,321–322tournament,319C-trail,315transniteinduction,213–214,395transitivegraph,55travellingsalesmanproblem,320tree,13–17binary,218,267cover,48–51,113asforcedsubstructure,15,179,202levelof,15normal,15–17,31,165,170innite,220,247,254,262,264,267,275,374,391-order,15packing,48–51,57–58,263,278,279424Indexpath-widthof,385ofseparations,362spanning:seespanningtree14,16,212,221topological,52,250–257,269,271,279topologicalinstandardsubspaces,270,271thresholdfunctionfor,342well-quasi-orderingoftrees,349–350treecoveringtheorem,49,263tree-decomposition,206,351–360,372–373,383,388–389of2-connectedgraphsinto3-conn'dpieces,62,384connected,360inducedonminors,352inducedonsubgraphs,352lean,359obstructions,355–359,360partof,351simplicial,351,384,388,391widthof,355treepackingtheorem,48,252tree-width,355–373andbrambles,355–359,386,388,389compactnesstheorem,387connected,360,384dualitytheorem,356,359nite,373andforbiddenminors,369–373ofgrid,359,385,388ofaminor,355obstructionstosmall,355–359,360ofasubdivision,384triangle,3triangulated,seechordaltriangulation,seeplanetriangulationtrivialgraph,2Trotter,W.
T.
,288,305Turan,P.
,175theorem,175,204,288graph,175–180,204Tutte,W.
T.
,42,48,57,62,63,64,65,85–86,109,117–118,154,157,164,171–172,238,247,278,311,321condition,41–42cyclebasistheorem,65,2791-factortheorem,42,57,240owconjectures,166–167,171planaritycriterion,109,117polynomial,172treepackingtheorem,48,57,252,278wheeltheorem,64–65,85–86Tychono'stheorem,216,274ubiquitous,222,265,276conjecture,222,265,276unfriendlypartitionconjecture,217,263,275uniformitylemma,seeregularitylemmaunion,3unitcircleS1,90,399universalgraphs,228–231,228,265,276unmatched,35up(-closureetc.
),15upperbound,394density,201Urquhart,A.
,147valency(degree),5valueofaow,152vanderWaerden,303variance,337Veldman,H.
J.
,321vertex,2-chromaticnumber,119colouring,119,122–127-connectivity,11cover,36,52–54cut,seeseparatorduplication,137expansion,137ofaplanegraph,90space,23-transitive,55,230,264Vizing,V.
G.
,128,148Voigt,M.
,148vortex,356,387Vuˇskovic,K.
,148Wagner,K.
,107,186,203,206,388'Wagner'sConjecture',seegraphminortheoremWagnergraph,186,353,384,390walk,10alternating,68closed,10length,10wave,233,266large,233limit,234Index425maximal,234proper,233small,233weaklyperfect,241,267well-foundedset,394well-ordering,394theorem,394well-quasi-ordering,347–391Welsh,D.
J.
A.
,172wheel,65,301,302theorem,65,85–86Whitney,H.
,86,102,113widthoftree-decomposition,355Wilson,R.
J.
,34Winkler,P.
,344Wollan,P.
,76,86,390–391Woodrow,R.
E.
,230,276Yu,X.
,58,321Zehavi,A.
,57Zorn'slemma,212,262,396Zykov,A.
A.
,204SymbolIndexTheentriesinthisindexaredividedintotwogroups.
Entriesinvolvingonlymathematicalsymbols(i.
e.
nolettersexceptvariables)arelistedontherstpage,groupedlooselybylogicalfunction.
Theentry'[]',forexample,referstothedenitionofinducedsubgraphsH[U]onpage4aswellastothedenitionoffaceboundariesG[f]onpage94.
Entriesinvolvingxedlettersasconstituentpartsarelistedonthesecondpage,intypographicalgroupsorderedalphabeticallybythoseletters.
Lettersstandingasvariablesareignoredintheordering.
2:=,=:3,=33331,36320+4,23,1544,92,154.
62∈2921∪,∩34,1,15||2,152,2452,187,259[]4,94,245[]k,[]<ω1,348,23/20,29C⊥,F⊥,.
.
.
240,1,2,.
.
.
1(n)k,.
.
.
328E(v),F(w)2E(X,Y),F(U,W)2(e,x,y),(u,v)150,245→E,→F,→C,.
.
.
150,156,158←e,←E,←F,.
.
.
150f(X,Y),g(U,W)150G,F,→e,.
.
.
110,156G2,H3,.
.
.
314G,X,P,.
.
.
4,150,246,369(S,S)152xy,x1.
.
.
xk,.
.
.
2,7xP,Px,xPy,xPyQz,.
.
.
7P,xQ,F,.
.
.
7,88,245xTy,.
.
.
14R.
Diestel,GraphTheory,GraduateTextsinMathematics173,DOI10.
1007/978-3-662-53622-3ReinhardDiestel2017427428SymbolIndexE327F21,23N1,393P325Zn1Zm*Zn161CG41C(G)24,254B(G)25,265E(G)23G(n,p)324KP,KP(S)374PH338Pi,j332V(G)23Ck,C(S,ω),C(S,ω)8,245E(G)2E(X)246F(G)92Forb369G(H1,H2)291IX19Kn3,211Kn1,.
.
.
,nr17Krs17L(G)4N(v),N(U)5N+(v)211Pk6PG144R(H)287R(H1,H2)287R(k,c,r)287R(r)285Rs196Sn92,399T2218TX19Tr1(n)175V(G)2V(X)246ch(G),ch(G)130col(G)122d(v),d(G)5d+(v)133d(x,y)8d(X,Y)187diam(G)8ex(n,H)175f(v)110g(G)8i1init(e)28log,ln1pw(G)385q(G)39rad(G)9tr1(n)175ter(e)28tw(G)355ve,vxy,vU20v(f)110Δ(G)5α(G)135δ(G)5ε(G),ε,ε(S)5,339,401κ(G)12κH(G)73λ(G)12λH(G)73μ337π:S2{(0,0,1)}→R292σk:Z→Zk157σ2337(G)157χ119,401χ(G)120χ(G)145ω(G),ω135,394Ω(G)2180,1393ReinhardDiestelreceivedaPhDfromtheUniversityofCambridge,follow-ingresearch1983–86asascholarofTrinityCollegeunderBelaBollobas.
HewasaFellowofSt.
John'sCollege,Cambridge,from1986to1990.
ResearchappointmentsandscholarshipshavetakenhimtoBielefeld(Germany),OxfordandtheUS.
HebecameaprofessorinChemnitzin1994andhasheldachairatHamburgsince1999.
ReinhardDiestel'smainareaofresearchisgraphtheory,includinginnitegraphtheory.
Hehaspublishednumerouspapersandaresearchmonograph,GraphDecompositions(Oxford1990).
简单测评v5.net的美国cn2云服务器:电信双程cn2+联通AS9929+移动直连
v5.net一直做独立服务器这块儿的,自从推出云服务器(VPS)以来站长一直还没有关注过,在网友的提醒下弄了个6G内存、2核、100G SSD的美国云服务器来写测评,主机测评给大家趟雷,让你知道v5.net的美国云服务器效果怎么样。本次测评数据仅供参考,有兴趣的还是亲自测试吧! 官方网站:https://v5.net/cloud.html 从显示来看CPU是e5-2660(2.2GHz主频),...
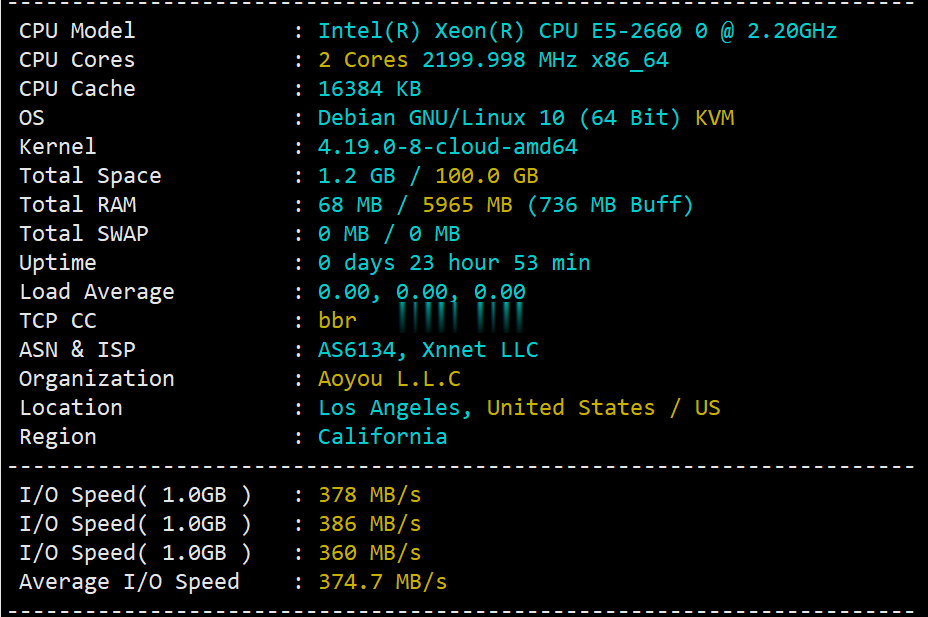
华纳云,3折低至优惠云服务器,独立服务器/高防御服务器低至6折,免备案香港云服务器CN2 GIA三网直连线路月付18元起,10Mbps带宽不限流量
近日华纳云发布了最新的618返场优惠活动,主要针对旗下的免备案香港云服务器、香港独立服务器、香港高防御服务器等产品,月付6折优惠起,高防御服务器可提供20G DDOS防御,采用E5处理器V4CPU性能,10Mbps独享CN2 GIA高速优质带宽,有需要免备案香港服务器、香港云服务器、香港独立服务器、香港高防御服务器、香港物理服务器的朋友可以尝试一下。华纳云好不好?华纳云怎么样?华纳云服务器怎么样?...

搬瓦工(季付46.7美元)新增荷兰(联通线路)VPS,2.5-10Gbps
搬瓦工最近新增了荷兰机房中国联通(AS9929、AS4837)线路的VPS产品,选项为NL - China Unicom Amsterdam(ENUL_9),与日本软银和洛杉矶(DC06)CN2 GIA配置一致可以互换,属于高端系列,2.5Gbps-10Gbps大带宽,最低季付46.7美元起。搬瓦工VPS隶属于老牌IT7公司旗下,主要提供基于KVM架构VPS主机,数据中心包括美国洛杉矶、凤凰城、纽...
openeuler为你推荐
-
ip购买急。购买一年的固定IP地址要多少钱?敬汉卿姓名被抢注如果有一定影响力的笔名,被某个产品抢注,能否起诉告其侵权?今日油条油条是怎样由来www.119mm.comwww.993mm+com精品集!16668.com香港最快开奖现场直播今晚开ww.66bobo.com有的网址直接输入***.com就行了,不用WWW, 为什么?朴容熙给我介绍几个韩国 ulzzang 最好是像柳惠珠那样的 不要出道的...弗雷德疯谁知百里挑一的冯晔炀的家乡在哪?他喜欢什么食物?喜欢去哪里旅游?苗惟妮大好时光演员表珊珊窝尚公寓窝尚公寓到底怎么样,谁玩过?