浮点定点和浮点的区别?
浮点 时间:2021-01-05 阅读:()
浮点数的解释
浮点数是属于有理数中某特定子集的数的数字表示,在计算机中用以近似表示任意某个实数。具体的说,这个实数由一个整数或定点数(即尾数)乘以某个基数(计算机中通常是2)的整数次幂得到,这种表示方法类似于基数为10的科学记数法。
浮点计算是指浮点数参与的运算,这种运算通常伴随着因为无法精确表示而进行的近似或舍入。
一个浮点数a由两个数m和e来表示:a = m × b^e。
在任意一个这样的系统中,我们选择一个基数b(记数系统的基)和精度p(即使用多少位来存储)。
m(即尾数)是形如±d.ddd...ddd的p位数(每一位是一个介于0到b-1之间的整数,包括0和b-1)。
如果m的第一位是非0整数,m称作规格化的。
有一些描述使用一个单独的符号位(s 代表+或者-)来表示正负,这样m必须是正的。
e是指数。
这种设计可以在某个固定长度的存储空间内表示定点数无法表示的更大范围的数。
例如,一个指数范围为±4的4位十进制浮点数可以用来表示43210,4.321或0.0004321,但是没有足够的精度来表示432.123和43212.3(必须近似为432.1和43210)。
当然,实际使用的位数通常远大于4。
此外,浮点数表示法通常还包括一些特别的数值:+∞和?∞(正负无穷大)以及NaN('Not a Number')。
无穷大用于数太大而无法表示的时候,NaN则指示非法操作或者无法定义的结果。
众所周知,计算机中的所有数据都是以二进制表示的,浮点数也不例外。
然而浮点数的二进制表示法却不像定点数那么简单了。
先澄清一个概念,浮点数并不一定等于小数,定点数也并不一定就是整数。
所谓浮点数就是小数点在逻辑上是不固定的,而定点数只能表示小数点固定的数值,具用浮点数或定点数表示某哪一种数要看用户赋予了这个数的意义是什么。
阶符是当一个数用科学计数法表示时,它的指数的符号,指数是正还是负,正负号就是阶符。
计算机机内数,当用科学计数法表示时,分尾数,指数,阶符3部分,阶符占1位,负为1,正为0。
C语言用e格式写数时 3.456e-03 就是 3.456 乘 10的负3次方, e后面的-号,就是阶符 正阶符,不写东西,或写+号。
3.456e03 就是 3.456 乘 10的正3次方, 浮点数的阶码可用补码或增码(移码)表示,数的表示范围是,在浮点表示方法中是隐含的 尾数是定点整数来的,尾数符号叫尾符
请高手通俗的讲一下浮点型是什么意思
百度说的不对, 浮点型就是有小数部分的数值, 整型就是没有小数部分的数值,c语言里面的浮点数的表示方法有几种?都是什么啊
2种表示方法 1.十进制小数形式,如1.08,.98,18.; 2.指数形式,如3.45e6 浮点数的类型分3类: 1.float,单精度浮点数,(visual C下)占用4个字节,表示范围:3.4e-38~3.4e38 2.double,双精度浮点数,占用8个字节,表示范围:1.7e-308~1.7e308 3.long double,长双精度浮点数,占用10个字节,表示范围:1.2e-4932~1.2e4932浮点数是啥
实型也称为浮点型。实型常量也称为实数或者浮点数。
在C语言中,实数只采用十进制。
它有二种形式:十进制小数形式,指数形式。
1) 十进制数形式:由数码0~ 9和小数点组成。
例如: 0.0、25.0、5.789、0.13、5.0、300.、-267.8230 等均为合法的实数。
注意,必须有小数点。
2) 指数形式:由十进制数,加阶码标志“e”或“E”以及阶码(只能为整数,可以带符号)组成。
其一般形式为: a E n(a为十进制数,n为十进制整数) 其值为 a*10n。
如: 2.1E5 (等于2.1*105) 3.7E-2 (等于3.7*10-2) 0.5E7 (等于0.5*107) -2.8E-2 (等于-2.8*10-2) 以下不是合法的实数: 345 (无小数点) E7 (阶码标志E之前无数字) -5 (无阶码标志) 53.-E3 (负号位置不对) 2.7E (无阶码) 标准C允许浮点数使用后缀。
后缀为“f”或“F”即表示该数为浮点数。
如356f和356.是等价的。
【例】说明了这种情况。
main(){ printf("%f ",356.); printf("%f ",356); printf("%f ",356f); } 实型变量 1. 实型数据在内存中的存放形式 实型数据一般占4个字节(32位)内存空间。
按指数形式存储。
实数3.14159在内存中的存放形式如下: + .314159 1 数符 小数部分 指数 ? 小数部分占的位(bit)数愈多,数的有效数字愈多,精度愈高。
? 指数部分占的位数愈多,则能表示的数值范围愈大。
2. 实型变量的分类 实型变量分为:单精度(float型)、双精度(double型)和长双精度(long double型)三类。
在Turbo C中单精度型占4个字节(32位)内存空间,其数值范围为3.4E-38~3.4E+38,只能提供七位有效数字。
双精度型占8 个字节(64位)内存空间,其数值范围为1.7E-308~1.7E+308,可提供16位有效数字。
定点和浮点的区别?
原发布者:yuanpan1987 计算机处理的数值数据多数带有小数,小数点在计算机中通常有两种表示方法,一种是约定所有数值数据的小数点隐含在某一个固定位置上,称为定点表示法,简称定点数;另一种是小数点位置可以浮动,称为浮点表示法,简称浮点数。1.定点数表示法(fixed-point)所谓定点格式,即约定机器中所有数据的小数点位置是固定不变的。
在计算机中通常采用两种简单的约定:将小数点的位置固定在数据的最高位之前,或者是固定在最低位之后。
一般常称前者为定点小数,后者为定点整数。
定点小数是纯小数,约定的小数点位置在符号位之后、有效数值部分最高位之前。
若数据?x?的形式为?x?=?x0.x1x2…xn?(?其中x0为符号位,x1~xn是数值的有效部分,也称为尾数,?x1为最高有效位?),则在计算机中的表示形式为:一般说来,如果最末位?xn?=1,前面各位都为?0?,则数的绝对值最小,即?|x|min?=2-n?。
如果各位均为?1,则数的绝对值最大,即?|x|max?=1-2-n?。
所以定点小数的表示范围是:2-?n??≤?|?x?|?≤?1-??2-?n定点整数是纯整数,约定的小数点位置在有效数值部分最低位之后。
若数据?x?的形式为?x?=?x0?x1x2…xn?(?其中x0为符号位,x1~xn?是尾数,?xn?为最低有效位?),则在计算机中的表示形式为:????定点整数的表示范围是:1≤?|?x?|?≤?2n??-??1当数据小于定点数能表示的最小值时,计算机将它们作0处理,称为下溢;大于定点数能表示的最大值时,计算机
- 浮点定点和浮点的区别?相关文档
- 信号北理工电子技术课程设计浮点频率计
- 小数PLC(FX2N)小数点(浮点)运算编程研究讲义
- 数据eeprom浮点存取方法
- 小数定点转浮点的Qn定义及计算公式方法
- 小数点将浮点型数据转换为字符串
- 数据串口通信中整型和浮点型数据的处理和发送
建站选择网站域名和IP主机地址之间关系和注意要点
今天中午的时候有网友联系到在选择网站域名建站和主机的时候问到域名和IP地址有没有关联,或者需要注意的问题。毕竟我们在需要建站的时候,我们需要选择网站域名和主机,而主机有虚拟主机,包括共享和独立IP,同时还有云服务器、独立服务器、站群服务器等形式。通过这篇文章,简单的梳理关于网站域名和IP之间的关系。第一、什么是域名所谓网站域名,就是我们看到的类似"www.laozuo.org",我们可以通过直接记...

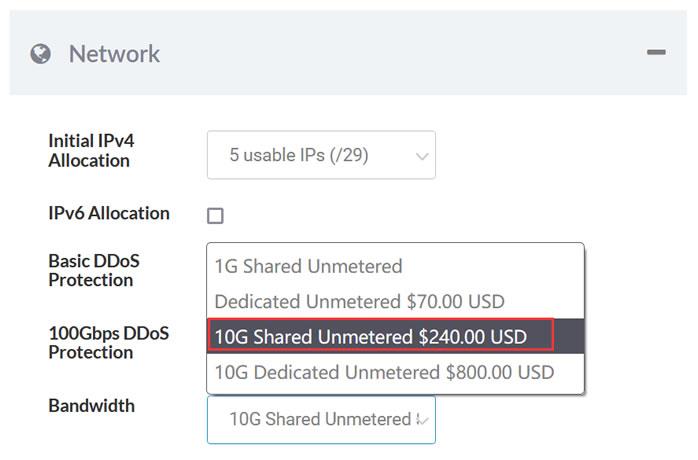
Sharktech10Gbps带宽,不限制流量,自带5个IPv4,100G防御
Sharktech荷兰10G带宽的独立服务器月付319美元起,10Gbps共享带宽,不限制流量,自带5个IPv4,免费60Gbps的 DDoS防御,可加到100G防御。CPU内存HDD价格购买地址E3-1270v216G2T$319/月链接E3-1270v516G2T$329/月链接2*E5-2670v232G2T$389/月链接2*E5-2678v364G2T$409/月链接这里我们需要注意,默...
天上云:香港大带宽物理机服务器572元;20Mbps带宽!三网CN2线路
天上云服务器怎么样?天上云是国人商家,成都天上云网络科技有限公司,专注于香港、美国海外云服务器的产品,有多年的运维维护经验。世界这么大 靠谱最重,我们7*24H为您提供服务,贴心售后服务,安心、省事儿、稳定、靠谱。目前,天上云香港大带宽物理机服务器572元;20Mbps带宽!三网CN2线路,香港沙田数据中心!点击进入:天上云官方网站地址香港沙田数据中心!线路说明 :去程中国电信CN2 +中国联通+...

浮点为你推荐
-
ddr2内存价格DDR2 1G内存 价格大概多少?``软银亏损65亿美元美国国际集团(AIG)上一季度亏损617亿美元英语词典哪个好哪个英语词典好电陶炉和电磁炉哪个好电陶炉和电磁炉哪个好空间登录qq如何在空间里登陆qq首选dns服务器地址什么是首选DNS服务器和备用DNS服务器?360云盘360云盘和微云那个好用?360云盘网页版360云盘网页版在哪里登录呀?广东联通官方旗舰店天猫上的广东移动官方旗舰店和移动真的有关系吗?10个比1688便宜的拿货网1688批发网上的东西怎么那么便宜啊 是不是骗人的呢