Links花生壳免费域名
花生壳免费域名 时间:2021-01-02 阅读:()
TheStructureofFreeDomainSemiringsP.
Jipsen,G.
StruthChapmanUSheeldApril9,2008P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20081/1OutlineIntroductionDomainSemiringsFreedomainsemiringRepresentationbybyantichainsofsequencesRepresentationbybinaryrelationsConclusionP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20082/1IntroductionAsemiringisoftheform(A,+,0,·,1)suchthat(A,+,0)isacommutativemonoid(A,·,1)isamonoid·distributesoverallnitejoinsfromtheleftandrighti.
e.
x(y+z)=xy+xz,(x+y)z=xz+yzandx0=0x=0Asemiringisidempotentifx+x=xISisthevarietyofidempotentsemiringsLemmaAnidempotentsemiringisa(join-)semilatticewith0asbottomelement,withx≤ygivenbyx+y=y(since+isassoc,commuandidempotent)andx≤y=wxz≤wyz(sincew(x+y)z=wxz+wyz)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20083/1ExamplesExamplesofsemiringsare:Rings(N,+,0,·,1).
.
.
Examplesofidempotentsemiringsare:Reductsofrelationalgebras(A,+,0,;,1)ReductsofKleenealgebras(A,+,0,·,1)Reductsofresiduatedlattices(A,1)(R∪{∞},max,0)Boundeddistributivelattices(A,∨,0,∧,1).
.
.
P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20084/1FreemonoidsandsemiringsLetXbeasetofvariables(orgenerators)ThefreemonoidoverXisX=n∈NXnwith1=emptysequenceand·asconcatenationBydistributivity,everytermtinthesignatureofsemiringscanbewrittenasanitejoinoftermsofthefreemonoidXExample:x(y+xz)(x+1)=xyx+xxzx+xy+xxzthefreeidempotentsemiringoverX,denotedbyFIS(X),isisomorphictothesetPn(X)ofallnitesubsetsofwordsoverXHereU+V=U∪VandU·V={uv:u∈U,v∈V}P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20085/1Decidabilitytheequationaltheoryofidempotentsemiringsisdecidable:Giventermss,t,usedistributivitytowritetermsinnormalformHowever,thequasiequationaltheory(=strictuniversalHorntheory)isundecidablebecause:Thewordproblemforsemigroupsisundecidable(Post)Everysemiringisasemigroupundertheoperation"·"EverysemigroupSisa"·"-subreductofitspowersetsemiringP(Se)(whereSethemonoidextensionofS)theclassof"·"-subreductsofsemiringsistheclassofallsemigroupsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20086/1DomainmonoidsAdomainmonoidisanalgebra(M,·,1,d)suchthat(M,·,1)isamonoidandd:M→Misafunctionthatsatises(D1)d(x)x=x(D2)d(xd(y))=d(xy)(D3)d(d(x)y)=d(x)d(y)(D4)d(x)d(y)=d(y)d(x)ThevarietiesofdomainmonoidsisdenotedbyDMLemmad(1)=1[takex=1in(D1)]d(d(x))=d(x)[takex=1in(D2)]d(x)d(x)=d(x)[takey=xin(D3)]d(M)={d(x):x∈M}isameetsemilatticewith1=topelementP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20087/1DomainsemiringsAdomainsemiringisanalgebra(A,+,0,·,1,d)suchthat(A,+,0,·,1)isasemiring(A,·,1,d)isadomainmonoidandthefollowingadditionalaxiomshold[Desharnais,Struth2008]d(x+y)=d(x)+d(y),d(0)=0andd(x)+1=1xd(x)+x=xx+x=xEverydomainsemiringisanidempotentsemiringThevarietiesofdomainsemiringsisdenotedbyDSP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20088/1ExamplesofdomainsemiringsExamplesofdomainsemiringsaree.
g.
reductsofrelationalgebraswithd(x)=(x;x)∧1,reductsofKleenealgebraswithdomainModelsofdomainsemiringsinCS:Idempotentsemiringsformedbysetsoftracesofaprogram(whicharealternatingsequencesofstateandactionsymbols)withdomaindenedbystartingstatesoftracesIdempotentsemiringsformedbysetsofpathsinagraphwithdomaindenedbysetsofstartingstatesApplicationsofdomainsemiringsandKleenealgebraswithdomainhavebeenstudiedintensivelyP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20089/1ApplicationsofdomainsemiringsThedomainoperationmodelsenablednessconditionsforactionsinprogramsandtransitionsystemsThedomainoperationcaneasilybeextendedintoamodaldiamondoperatorthatactsontheunderlyingalgebraofdomainelements[M¨oller,Struth2006]Linksthealgebraicapproachwithmoretraditionallogicsofprogramssuchasdynamic,temporalandHoarelogicsSomestandardsemanticsofprograms,includingtheweakestpreconditionandweakestliberalpreconditionsemantics,canbemodeledinthissettingApplicationscanbefoundinRelMiCSconferenceproceedingsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200810/1DomainsemiringsDomainsemiringswereoriginallyintroducedinatwo-sortedsettingThedomainoperationmapsarbitrarysemiringelementstoaspecialBooleansubalgebra[Desharnais,M¨oller,Struth2006]ArbitrarysemiringelementsmodelactionsofaprogramortransitionsystemTheelementsoftheBooleansubalgebramodelthestatesofthatsystemHereweusethesimplerandmoregeneralone-sortedapproachof[Desharnais,Struth2008]P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200811/1StudyingfreedomainsemiringsThefreedomainsemiringisinterestingforapplications:IdentiesexactlythosetermsofdomainsemiringsthathavethesamedenotationinalldomainsemiringsAllowsthedenitionofecientproofanddecisionproceduresThedomainaxiomsofdomainsemiringsarethesameasforrelationalgebrasandforKleenealgebraswithdomainBothrelationalgebrasandKleenealgebrashaverichandcomplex(quasi)equationaltheoriesRatherstudythesimplerequationaltheoryofdomainsemiringsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200812/1OutlineofresultsAim:giveanexplicitdescriptionoffreedomainsemiringsFDS(X)FirstdescribefreedomainmonoidFDM(X)ThenshowthattheseelementsarethejoinirreduciblesofFDS(X)FDS(X)isisomorphictothesetofniteantichainsintheposetofjoinirreduciblesShowFDS(X)isrepresentablebyaconcretealgebraofbinaryrelations,withrelationaldomainasoperationsDS=HSP{Relationaldomainsemirings}Finallyshowanydistributivelatticewithni-aryoperatorsoccursasdomainelementsofsomedomainsemiringwithni1-aryoperatorsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200813/1One-generateddomainterms(D1)d(x)x=x(D2)d(xd(y))=d(xy)(D3)d(d(x)y)=d(x)d(y)Asusual,wedenex0=1andxn+1=xnxLemmaInadomainmonoid,ifm≤nthend(xm)xn=xnandd(xm)d(xn)=d(xn)Proof.
Assumingm≤n,wewritexn=xmxnm,andusing(D1)wehaved(xm)xn=d(xm)xmxnm=xmxnm=xnNow(D3)impliesd(xm)d(xn)=d(d(xm)xn)=d(xn)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200814/1ExpandednormalformsOnelementsoftheformd(xj),theorderisinducedbythemeet-semilatticestructure:d(xj)≤d(xk)ij≥k,hencetheseelementsformachainForconcatenationsofbasicterms,rewritetheminexpandednormalform:d(xj0)xd(xj1)xd(xj2)x···xd(xjm)whereeachofthejk≥max{1+jk+1,2+jk+2,mk+jm}E.
g.
xd(x3)x2d(x2)=.
.
.
P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200815/1DecreasingsequencesofnumbersForbrevitydenotesuchatermbythesequence(j0,j1,j2,jm)NotethatthisisalwaysastrictlydecreasingsequenceofnonnegativeintegersLetP=(P,≤)bethesetofallsuchsequences,orderedbyreversepointwiseorderThussequencesofdierentlengtharenotcomparable,andthemaximalelementsofthisposetare(0),(1,0),(2,1,0),.
.
.
correspondingtothetermsd(1)=1,d(x)xd(1)=x,d(x2)xd(x)xd(1)=x2,.
.
.
P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200816/1Theposetofjoin-irreduciblesbelow1andxd(x5)d(x4)d(x3)d(x2)d(x1)1=d(x0)(5)(4)(3)(2)(1)(0).
.
.
xd(x2)xd(x3)xd(x4)xd(x5)xd(x6)x(1,0)(2,0)(3,0)(4,0)(5,0)(6,0).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
d(x6)xd(x)d(x6)xd(x2)d(x6)xd(x3)d(x6)xd(x4)xd(x5)(6,1)(6,2)(6,3)(6,4)(6,5)(5,4)=xd(x4)(4,3)=xd(x3)(3,2)=xd(x2)(2,1)=xd(x)(5,3)=d(x5)xd(x3)(4,2)=d(x4)xd(x2)(3,1)=d(x3)xd(x)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200817/1Theposetofjoin-irreduciblesbelowx2x2=(2,1,0)(3,1,0)(4,1,0)(5,1,0)(6,1,0).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(6,2,0)(6,3,0)(6,4,0)(6,5,0).
.
.
.
.
.
.
.
.
.
.
.
(6,4,3)(5,3,2)(4,2,1)(3,2,1)(4,3,2)(5,4,3)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200818/1TheproductoftwodecreasingsequencesAmultiplicationisdenedonPbythefollowing"rippleproduct"(j0,j1,j2,jm)·(k0,k1,k2,kn)=(j′0,j′1,j′2,j′m,k1,k2,kn)wherej′m=max(jm,k0)andj′i=max(ji,j′i+1+1)fori=m1,2,1,0Forexample,(7,3,2)·(4,3,1)=(7,5,4,3,1),while(4,3,1)·(7,3,2)=(9,8,7,3,2)CanshowthatthisistheresultofmultiplyingthecorrespondingexpandednormalformsandrewritingresultinexpandednormalformItistediousbutnotdiculttocheckthatthisoperationisassociativeP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200819/1DomainandpartialorderThedomainofasequence(j0,j1,j2,jm)isthelength-onesequence(j0)Thiscorrespondstothedomaintermd(xj0)LetA(P)bethesetofniteantichainsofPApartialorderisdenedonA(P)bya≤bi↓a↓bThemultiplicationisextendedtoantichainsbyusingthecomplexproduct(i.
e.
U·V={uv:u∈U,v∈V})andbyremovingallnon-maximalelementsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200820/1RepresentationTheoremTherstresultshowsthattheone-generatedfreedomainsemiringcanberepresentedintermsofantichainsofdecreasingintegersequencesTheoremThejoinirreduciblesofFDS(x)formaposetthatisisomorphictoPandFDS(x)isisomorphictoA(P)Proof.
(outline)Bydistributivity,eachdomainsemiringtermt(x)canbewrittenasanitejoinofexpandednormalformtermsHenceanyjoinirreducibleelementofFDS(x)canberepresentedbyanexpandednormalformtermToshowthatPistheposetofthesejoinirreducible,itsucestoshowthatallexpandednormalformsarejoinirreducible,andthattwoexpandednormalformtermscanbedistinguishedinsomedomainmonoid(detailsinproceedings)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200821/1Exampletermandrelationforj=(4,3,1)j=(4,3,1)tj(x)=d(x4)xd(x3)xd(x)(s)(f)Xj={arrows}P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200822/1RepresentionofsemiringsbybinaryrelationsFirstnotethatforfreeidempotentsemiringsthisisalwayspossible[Bredihin,Schein1978]ForasetXofgenerators,aconcreteconstructioncanbeobtainedbyconsideringthecomplexalgebraofthefreegroupFGrp(X)Thisisalwaysarepresentablerelationalgebra,withtheelementsofthegroupasdisjointrelationsSincethefreemonoidXisasubsetofthefreegroup,theniteunionsoftherelationscorrespondingtosingletonwordsgivearelationalrepresentationofthefreeidempotentsemiringwithXassetofgeneratorsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200823/1RepresentionofsemiringsbybinaryrelationsHowever,notallidempotentsemiringscanberepresentedby∪,semiringsofrelations[Andreka1988,1991]showedthattheclassofalgebrasofrelations,closedunder∪,,thoughdenablebyquasiequations,isnotnitelyaxiomatisableHenceitisstrictlysmallerthanthenitelybasedvarietyofidempotentsemiringsSimilarlytheclassofalgebrasofrelationsclosedunderid,d,whered(R)=R;R∩id,isanon-nitelyaxiomatisablequasivariety,butnotavarietyP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200824/1RepresentionofsemiringsbybinaryrelationsTheoremTheone-generatedfreedomainsemiringcanberepresentedbyadomainsemiringofbinaryrelationsProof.
(outline)ToseethatFDS(x)canberepresentedbyacollectionofbinaryrelations,withoperationsofunion,compositionanddomain,itsucestoconstructarelationXonasetUsuchthats(X)=t(X)intherelationdomainsemiringP(U*U)foranydistinctpairofelementsofFDS(x)Thisisdonesimilarlytotheproofoftheprecedingtheorem,bytakingXtobetheunion(overdisjointbasesets)ofalltherelationsXjcorrespondingtothesequencesj∈PP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200825/1n-generatedcase(briey)Sofarouranalysishasconsideredtheone-generatedfreedomainsemiringThen-generatedcaseismorecomplex,buthasrecentlyalsobeenhandledAnormalformisgivenbyd(t0)y1d(t1)y2.
.
.
d(tn1)ynd(tn)wheretiarereducedtermsNormalformisgivenbyareducedtreeRelationalrepresentationsimilartotheone-generatedcaseFutureresearchisalsoaimingtodescribethestructureoffreedomainsemiringsinthepresenceofadditionalaxioms[Desharnais,Struth2008]showthatthedomainalgebrasd(S)inducedbythedomainaxiomscanbeturnedinto(co-)HeytingalgebrasorBooleanalgebrasbyimposingfurtherconstraintsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200826/1Anti-domainInparticular,addingthethreeaxiomsa(x)x=0,a(xy)≤a(xa(a(y)))anda(a(x))+a(x)=1foranantidomainfunctiona:S→Stothesemiringaxiomsanddeningdomainasd(x)=a(a(x))sucestoensured(S)isaBooleanalgebrarecoveralltheoremsoftheoriginaltwo-sortedaxiomatisationof[Desharnais,M¨oller,Struth2006]Basedontheseresults,inparticularthestructureofthefreeBooleandomainsemiringscertainlydeservefurtherinvestigationP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200827/1BooleandomainsemiringsgeneralizeJonsson-TarskiBAOs|xp=d(xp)isamodaloperatorond(A)Ingeneralfisanoperatoriffx+y,fx,fy,andf0,0BAO=BAwithoperatorsB=(B,+,0,·,1,,(fi)i∈I)BDSO=BooleanDSwithoperatorsA=(A,+,0,·,1,a,(gi)i∈I)Dened(A)=(a(a(A)),+,0,·,1,a,(|gi)i∈I)where|gi(p0,pn)=a(a(gi(p0,pn1)·pn))TheoremForanyBAOBthereexistsaBooleanDSOAsuchthatB=d(A)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200828/1DomainsemiringsgeneralizeGehrke-JonssonDLOsDLO=bnddistributivelatticeswithoperatorsB=(B,+,0,·,1,,(fi)i∈I)DSO=domainsemiringswithoperatorsA=(A,+,0,·,1,d,(gi)i∈I)Dened(A)=(d(A),+,0,·,1,d,(|gi)i∈I)where|gi(p0,pn)=d(gi(p0,pn1)·pn)TheoremForanyDLOBthereexistsaDSOAsuchthatB=d(A)Aisconstructedfromtherelationaldomainsemiringonthejoin-irreduciblesofthecanonicalextensionofBConclusion:DomainsemiringsgiveasimpleunisortedextensionofthestaticpropositionalframeworktothedynamicframeworkofsequencesP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200829/1References[H.
Andreka1989]Ontherepresentationproblemofdistributivesemilattice-orderedsemigroups,preprint(1988),AbstractsoftheAMS,Vol10,No2(March1989),p.
174.
[H.
Andreka1991]Representationsofdistributivelattice-orderedsemigroupswithbinaryrelations,AlgebraUniversalis28(1991),12–25.
[G.
Birkho1967]"LatticeTheory",3rded.
,Vol25ofAMSColloquiumPublications,AMS,1967,pp.
viii+420.
[D.
A.
Bredihin,B.
M.
Schein1978]Representationsoforderedsemigroupsandlatticesbybinaryrelations,Colloq.
Math.
39(1978),1–12.
[J.
Desharnais,B.
M¨oller,G.
Struth2006]Kleenealgebrawithdomain,ACMTransactionsonComputationalLogic,Vol7,No4,2006,798–833.
[J.
Desharnais,G.
Struth2008]ModalSemiringsRevisited,ResearchReportCS-08-01,DepartmentofComputerScience,TheUniversityofSheeld,2008.
[W.
McCune2007]Prover9,www.
prover9.
org[B.
M¨oller,G.
Struth2006]Algebrasofmodaloperatorsandpartialcorrectness,TheoreticalComputerScience,351,(2006),221–239.
P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200830/1
Jipsen,G.
StruthChapmanUSheeldApril9,2008P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20081/1OutlineIntroductionDomainSemiringsFreedomainsemiringRepresentationbybyantichainsofsequencesRepresentationbybinaryrelationsConclusionP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20082/1IntroductionAsemiringisoftheform(A,+,0,·,1)suchthat(A,+,0)isacommutativemonoid(A,·,1)isamonoid·distributesoverallnitejoinsfromtheleftandrighti.
e.
x(y+z)=xy+xz,(x+y)z=xz+yzandx0=0x=0Asemiringisidempotentifx+x=xISisthevarietyofidempotentsemiringsLemmaAnidempotentsemiringisa(join-)semilatticewith0asbottomelement,withx≤ygivenbyx+y=y(since+isassoc,commuandidempotent)andx≤y=wxz≤wyz(sincew(x+y)z=wxz+wyz)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20083/1ExamplesExamplesofsemiringsare:Rings(N,+,0,·,1).
.
.
Examplesofidempotentsemiringsare:Reductsofrelationalgebras(A,+,0,;,1)ReductsofKleenealgebras(A,+,0,·,1)Reductsofresiduatedlattices(A,1)(R∪{∞},max,0)Boundeddistributivelattices(A,∨,0,∧,1).
.
.
P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20084/1FreemonoidsandsemiringsLetXbeasetofvariables(orgenerators)ThefreemonoidoverXisX=n∈NXnwith1=emptysequenceand·asconcatenationBydistributivity,everytermtinthesignatureofsemiringscanbewrittenasanitejoinoftermsofthefreemonoidXExample:x(y+xz)(x+1)=xyx+xxzx+xy+xxzthefreeidempotentsemiringoverX,denotedbyFIS(X),isisomorphictothesetPn(X)ofallnitesubsetsofwordsoverXHereU+V=U∪VandU·V={uv:u∈U,v∈V}P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20085/1Decidabilitytheequationaltheoryofidempotentsemiringsisdecidable:Giventermss,t,usedistributivitytowritetermsinnormalformHowever,thequasiequationaltheory(=strictuniversalHorntheory)isundecidablebecause:Thewordproblemforsemigroupsisundecidable(Post)Everysemiringisasemigroupundertheoperation"·"EverysemigroupSisa"·"-subreductofitspowersetsemiringP(Se)(whereSethemonoidextensionofS)theclassof"·"-subreductsofsemiringsistheclassofallsemigroupsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20086/1DomainmonoidsAdomainmonoidisanalgebra(M,·,1,d)suchthat(M,·,1)isamonoidandd:M→Misafunctionthatsatises(D1)d(x)x=x(D2)d(xd(y))=d(xy)(D3)d(d(x)y)=d(x)d(y)(D4)d(x)d(y)=d(y)d(x)ThevarietiesofdomainmonoidsisdenotedbyDMLemmad(1)=1[takex=1in(D1)]d(d(x))=d(x)[takex=1in(D2)]d(x)d(x)=d(x)[takey=xin(D3)]d(M)={d(x):x∈M}isameetsemilatticewith1=topelementP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20087/1DomainsemiringsAdomainsemiringisanalgebra(A,+,0,·,1,d)suchthat(A,+,0,·,1)isasemiring(A,·,1,d)isadomainmonoidandthefollowingadditionalaxiomshold[Desharnais,Struth2008]d(x+y)=d(x)+d(y),d(0)=0andd(x)+1=1xd(x)+x=xx+x=xEverydomainsemiringisanidempotentsemiringThevarietiesofdomainsemiringsisdenotedbyDSP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20088/1ExamplesofdomainsemiringsExamplesofdomainsemiringsaree.
g.
reductsofrelationalgebraswithd(x)=(x;x)∧1,reductsofKleenealgebraswithdomainModelsofdomainsemiringsinCS:Idempotentsemiringsformedbysetsoftracesofaprogram(whicharealternatingsequencesofstateandactionsymbols)withdomaindenedbystartingstatesoftracesIdempotentsemiringsformedbysetsofpathsinagraphwithdomaindenedbysetsofstartingstatesApplicationsofdomainsemiringsandKleenealgebraswithdomainhavebeenstudiedintensivelyP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,20089/1ApplicationsofdomainsemiringsThedomainoperationmodelsenablednessconditionsforactionsinprogramsandtransitionsystemsThedomainoperationcaneasilybeextendedintoamodaldiamondoperatorthatactsontheunderlyingalgebraofdomainelements[M¨oller,Struth2006]Linksthealgebraicapproachwithmoretraditionallogicsofprogramssuchasdynamic,temporalandHoarelogicsSomestandardsemanticsofprograms,includingtheweakestpreconditionandweakestliberalpreconditionsemantics,canbemodeledinthissettingApplicationscanbefoundinRelMiCSconferenceproceedingsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200810/1DomainsemiringsDomainsemiringswereoriginallyintroducedinatwo-sortedsettingThedomainoperationmapsarbitrarysemiringelementstoaspecialBooleansubalgebra[Desharnais,M¨oller,Struth2006]ArbitrarysemiringelementsmodelactionsofaprogramortransitionsystemTheelementsoftheBooleansubalgebramodelthestatesofthatsystemHereweusethesimplerandmoregeneralone-sortedapproachof[Desharnais,Struth2008]P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200811/1StudyingfreedomainsemiringsThefreedomainsemiringisinterestingforapplications:IdentiesexactlythosetermsofdomainsemiringsthathavethesamedenotationinalldomainsemiringsAllowsthedenitionofecientproofanddecisionproceduresThedomainaxiomsofdomainsemiringsarethesameasforrelationalgebrasandforKleenealgebraswithdomainBothrelationalgebrasandKleenealgebrashaverichandcomplex(quasi)equationaltheoriesRatherstudythesimplerequationaltheoryofdomainsemiringsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200812/1OutlineofresultsAim:giveanexplicitdescriptionoffreedomainsemiringsFDS(X)FirstdescribefreedomainmonoidFDM(X)ThenshowthattheseelementsarethejoinirreduciblesofFDS(X)FDS(X)isisomorphictothesetofniteantichainsintheposetofjoinirreduciblesShowFDS(X)isrepresentablebyaconcretealgebraofbinaryrelations,withrelationaldomainasoperationsDS=HSP{Relationaldomainsemirings}Finallyshowanydistributivelatticewithni-aryoperatorsoccursasdomainelementsofsomedomainsemiringwithni1-aryoperatorsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200813/1One-generateddomainterms(D1)d(x)x=x(D2)d(xd(y))=d(xy)(D3)d(d(x)y)=d(x)d(y)Asusual,wedenex0=1andxn+1=xnxLemmaInadomainmonoid,ifm≤nthend(xm)xn=xnandd(xm)d(xn)=d(xn)Proof.
Assumingm≤n,wewritexn=xmxnm,andusing(D1)wehaved(xm)xn=d(xm)xmxnm=xmxnm=xnNow(D3)impliesd(xm)d(xn)=d(d(xm)xn)=d(xn)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200814/1ExpandednormalformsOnelementsoftheformd(xj),theorderisinducedbythemeet-semilatticestructure:d(xj)≤d(xk)ij≥k,hencetheseelementsformachainForconcatenationsofbasicterms,rewritetheminexpandednormalform:d(xj0)xd(xj1)xd(xj2)x···xd(xjm)whereeachofthejk≥max{1+jk+1,2+jk+2,mk+jm}E.
g.
xd(x3)x2d(x2)=.
.
.
P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200815/1DecreasingsequencesofnumbersForbrevitydenotesuchatermbythesequence(j0,j1,j2,jm)NotethatthisisalwaysastrictlydecreasingsequenceofnonnegativeintegersLetP=(P,≤)bethesetofallsuchsequences,orderedbyreversepointwiseorderThussequencesofdierentlengtharenotcomparable,andthemaximalelementsofthisposetare(0),(1,0),(2,1,0),.
.
.
correspondingtothetermsd(1)=1,d(x)xd(1)=x,d(x2)xd(x)xd(1)=x2,.
.
.
P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200816/1Theposetofjoin-irreduciblesbelow1andxd(x5)d(x4)d(x3)d(x2)d(x1)1=d(x0)(5)(4)(3)(2)(1)(0).
.
.
xd(x2)xd(x3)xd(x4)xd(x5)xd(x6)x(1,0)(2,0)(3,0)(4,0)(5,0)(6,0).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
d(x6)xd(x)d(x6)xd(x2)d(x6)xd(x3)d(x6)xd(x4)xd(x5)(6,1)(6,2)(6,3)(6,4)(6,5)(5,4)=xd(x4)(4,3)=xd(x3)(3,2)=xd(x2)(2,1)=xd(x)(5,3)=d(x5)xd(x3)(4,2)=d(x4)xd(x2)(3,1)=d(x3)xd(x)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200817/1Theposetofjoin-irreduciblesbelowx2x2=(2,1,0)(3,1,0)(4,1,0)(5,1,0)(6,1,0).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(6,2,0)(6,3,0)(6,4,0)(6,5,0).
.
.
.
.
.
.
.
.
.
.
.
(6,4,3)(5,3,2)(4,2,1)(3,2,1)(4,3,2)(5,4,3)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200818/1TheproductoftwodecreasingsequencesAmultiplicationisdenedonPbythefollowing"rippleproduct"(j0,j1,j2,jm)·(k0,k1,k2,kn)=(j′0,j′1,j′2,j′m,k1,k2,kn)wherej′m=max(jm,k0)andj′i=max(ji,j′i+1+1)fori=m1,2,1,0Forexample,(7,3,2)·(4,3,1)=(7,5,4,3,1),while(4,3,1)·(7,3,2)=(9,8,7,3,2)CanshowthatthisistheresultofmultiplyingthecorrespondingexpandednormalformsandrewritingresultinexpandednormalformItistediousbutnotdiculttocheckthatthisoperationisassociativeP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200819/1DomainandpartialorderThedomainofasequence(j0,j1,j2,jm)isthelength-onesequence(j0)Thiscorrespondstothedomaintermd(xj0)LetA(P)bethesetofniteantichainsofPApartialorderisdenedonA(P)bya≤bi↓a↓bThemultiplicationisextendedtoantichainsbyusingthecomplexproduct(i.
e.
U·V={uv:u∈U,v∈V})andbyremovingallnon-maximalelementsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200820/1RepresentationTheoremTherstresultshowsthattheone-generatedfreedomainsemiringcanberepresentedintermsofantichainsofdecreasingintegersequencesTheoremThejoinirreduciblesofFDS(x)formaposetthatisisomorphictoPandFDS(x)isisomorphictoA(P)Proof.
(outline)Bydistributivity,eachdomainsemiringtermt(x)canbewrittenasanitejoinofexpandednormalformtermsHenceanyjoinirreducibleelementofFDS(x)canberepresentedbyanexpandednormalformtermToshowthatPistheposetofthesejoinirreducible,itsucestoshowthatallexpandednormalformsarejoinirreducible,andthattwoexpandednormalformtermscanbedistinguishedinsomedomainmonoid(detailsinproceedings)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200821/1Exampletermandrelationforj=(4,3,1)j=(4,3,1)tj(x)=d(x4)xd(x3)xd(x)(s)(f)Xj={arrows}P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200822/1RepresentionofsemiringsbybinaryrelationsFirstnotethatforfreeidempotentsemiringsthisisalwayspossible[Bredihin,Schein1978]ForasetXofgenerators,aconcreteconstructioncanbeobtainedbyconsideringthecomplexalgebraofthefreegroupFGrp(X)Thisisalwaysarepresentablerelationalgebra,withtheelementsofthegroupasdisjointrelationsSincethefreemonoidXisasubsetofthefreegroup,theniteunionsoftherelationscorrespondingtosingletonwordsgivearelationalrepresentationofthefreeidempotentsemiringwithXassetofgeneratorsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200823/1RepresentionofsemiringsbybinaryrelationsHowever,notallidempotentsemiringscanberepresentedby∪,semiringsofrelations[Andreka1988,1991]showedthattheclassofalgebrasofrelations,closedunder∪,,thoughdenablebyquasiequations,isnotnitelyaxiomatisableHenceitisstrictlysmallerthanthenitelybasedvarietyofidempotentsemiringsSimilarlytheclassofalgebrasofrelationsclosedunderid,d,whered(R)=R;R∩id,isanon-nitelyaxiomatisablequasivariety,butnotavarietyP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200824/1RepresentionofsemiringsbybinaryrelationsTheoremTheone-generatedfreedomainsemiringcanberepresentedbyadomainsemiringofbinaryrelationsProof.
(outline)ToseethatFDS(x)canberepresentedbyacollectionofbinaryrelations,withoperationsofunion,compositionanddomain,itsucestoconstructarelationXonasetUsuchthats(X)=t(X)intherelationdomainsemiringP(U*U)foranydistinctpairofelementsofFDS(x)Thisisdonesimilarlytotheproofoftheprecedingtheorem,bytakingXtobetheunion(overdisjointbasesets)ofalltherelationsXjcorrespondingtothesequencesj∈PP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200825/1n-generatedcase(briey)Sofarouranalysishasconsideredtheone-generatedfreedomainsemiringThen-generatedcaseismorecomplex,buthasrecentlyalsobeenhandledAnormalformisgivenbyd(t0)y1d(t1)y2.
.
.
d(tn1)ynd(tn)wheretiarereducedtermsNormalformisgivenbyareducedtreeRelationalrepresentationsimilartotheone-generatedcaseFutureresearchisalsoaimingtodescribethestructureoffreedomainsemiringsinthepresenceofadditionalaxioms[Desharnais,Struth2008]showthatthedomainalgebrasd(S)inducedbythedomainaxiomscanbeturnedinto(co-)HeytingalgebrasorBooleanalgebrasbyimposingfurtherconstraintsP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200826/1Anti-domainInparticular,addingthethreeaxiomsa(x)x=0,a(xy)≤a(xa(a(y)))anda(a(x))+a(x)=1foranantidomainfunctiona:S→Stothesemiringaxiomsanddeningdomainasd(x)=a(a(x))sucestoensured(S)isaBooleanalgebrarecoveralltheoremsoftheoriginaltwo-sortedaxiomatisationof[Desharnais,M¨oller,Struth2006]Basedontheseresults,inparticularthestructureofthefreeBooleandomainsemiringscertainlydeservefurtherinvestigationP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200827/1BooleandomainsemiringsgeneralizeJonsson-TarskiBAOs|xp=d(xp)isamodaloperatorond(A)Ingeneralfisanoperatoriffx+y,fx,fy,andf0,0BAO=BAwithoperatorsB=(B,+,0,·,1,,(fi)i∈I)BDSO=BooleanDSwithoperatorsA=(A,+,0,·,1,a,(gi)i∈I)Dened(A)=(a(a(A)),+,0,·,1,a,(|gi)i∈I)where|gi(p0,pn)=a(a(gi(p0,pn1)·pn))TheoremForanyBAOBthereexistsaBooleanDSOAsuchthatB=d(A)P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200828/1DomainsemiringsgeneralizeGehrke-JonssonDLOsDLO=bnddistributivelatticeswithoperatorsB=(B,+,0,·,1,,(fi)i∈I)DSO=domainsemiringswithoperatorsA=(A,+,0,·,1,d,(gi)i∈I)Dened(A)=(d(A),+,0,·,1,d,(|gi)i∈I)where|gi(p0,pn)=d(gi(p0,pn1)·pn)TheoremForanyDLOBthereexistsaDSOAsuchthatB=d(A)Aisconstructedfromtherelationaldomainsemiringonthejoin-irreduciblesofthecanonicalextensionofBConclusion:DomainsemiringsgiveasimpleunisortedextensionofthestaticpropositionalframeworktothedynamicframeworkofsequencesP.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200829/1References[H.
Andreka1989]Ontherepresentationproblemofdistributivesemilattice-orderedsemigroups,preprint(1988),AbstractsoftheAMS,Vol10,No2(March1989),p.
174.
[H.
Andreka1991]Representationsofdistributivelattice-orderedsemigroupswithbinaryrelations,AlgebraUniversalis28(1991),12–25.
[G.
Birkho1967]"LatticeTheory",3rded.
,Vol25ofAMSColloquiumPublications,AMS,1967,pp.
viii+420.
[D.
A.
Bredihin,B.
M.
Schein1978]Representationsoforderedsemigroupsandlatticesbybinaryrelations,Colloq.
Math.
39(1978),1–12.
[J.
Desharnais,B.
M¨oller,G.
Struth2006]Kleenealgebrawithdomain,ACMTransactionsonComputationalLogic,Vol7,No4,2006,798–833.
[J.
Desharnais,G.
Struth2008]ModalSemiringsRevisited,ResearchReportCS-08-01,DepartmentofComputerScience,TheUniversityofSheeld,2008.
[W.
McCune2007]Prover9,www.
prover9.
org[B.
M¨oller,G.
Struth2006]Algebrasofmodaloperatorsandpartialcorrectness,TheoreticalComputerScience,351,(2006),221–239.
P.
Jipsen,G.
Struth(ChapmanUSheeld)FreeDomainSemiringsApril9,200830/1
- Links花生壳免费域名相关文档
- 设置花生壳免费域名
- 投标人花生壳免费域名
- 地址花生壳免费域名
- 花生壳免费域名--花生壳绑定tomcat 花生壳路由器的设置
- 花生壳花生壳动态域名使用方法详解(免费动态域名)
- 花生壳通过花生壳服务申请免费域名
GigsGigsCloud 春节优惠2022 指定云服务器VPS主机85折循环优惠码
GigsGigsCloud商家在之前介绍的还是比较多的,因为之前我一直有几台机器在使用,只是最近几年网站都陆续转型删除掉不少的网站和闲置域名,包括今年也都减少网站开始转型自媒体方向。GigsGigsCloud 商家产品还是比较有特色的,有提供香港、新加坡等亚洲机房的云服务器、VPS和独立服务器等。第一、新春优惠活动优惠码:CNY2022-15OFF截止到正月初二,我们可以使用上述优惠码在购买指定G...

修罗云50元/月起香港大宽带NAT VPS,香港沙田建站2核2G5M仅70元/月起
修罗云怎么样?修罗云是一家国内老牌商家,修罗云商家以销售NAT机器起家,国内的中转机相当不错,给的带宽都非常高,此前推荐的也都是国内NAT VPS机器。今天,云服务器网(www.yuntue.com)小编主要介绍一下修罗云的香港云服务器,适合建站,香港沙田cn2云服务器,2核2G,5M带宽仅70元/月起,同时香港香港大带宽NAT VPS低至50元/月起,性价比不错,可以尝试一下!点击进入:修罗云官...

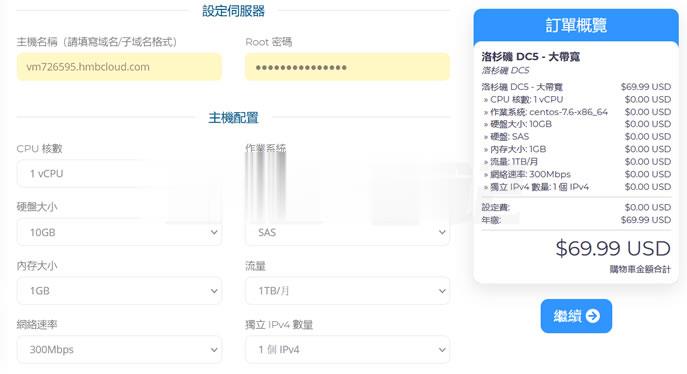
半月湾hmbcloud升级500Mbps带宽,原生VPS,$4.99/月
关于半月湾HMBCloud商家之前也有几篇那文章介绍过这个商家的产品,对于他们家的其他产品我都没有多加留意,而是对他们家的DC5机房很多人还是比较喜欢的,这个比我们有些比较熟悉的某商家DC6 DC9机房限时,而且半月湾HMBCloud商家是相对便宜的。关于半月湾DC5机房的方案选择和介绍:1、半月湾三网洛杉矶DC5 CN2 GIA同款DC6 DC9 1G内存 1TB流量 月$4.992、亲测选择半...
花生壳免费域名为你推荐
-
国内虚拟主机国内最好的虚拟主机虚拟空间购买现在网上有些虚拟空间很便宜,30元/就有100M,值得信不?php虚拟主机如何选择PHP网站虚拟主机vps虚拟主机虚拟主机和VPS的主要区别有哪些?主要是哪些参数不一样?便宜的虚拟主机低价虚拟主机那种类型的好呢?香港虚拟空间香港虚拟空间哪家好?手机网站空间谁有上手机网站刷空间人气的网址网站空间免备案哪里能找到免费、免备案的空间?虚拟主机mysql怎么管理虚拟主机上的MYSQL?(高分回报)深圳虚拟主机深圳鼎峰网络科技 虚拟主机空间怎么样