rected27eee.com
27eee.com 时间:2021-03-24 阅读:()
ProgrammingG.
K.
ManacherTechniquesEditorComputingConnectedComponentsonParallelComputersD.
S.
HirschbergRiceUniversityA.
K.
ChandraIBMThomasJ.
WatsonResearchCenterD.
V.
SarwateUniversityofIllinoismotivatedinpartbypracticalconsiderations.
Amongthemanyareastreatedintherecentliteraturearesorting[2,3,7,12,15],theevaluationofarithmeticexpressions,linearrecurrencesandpolynomials[4,8,10],matrixalgorithms[5,6,13],andgraphtheory[9,14,15].
InthispaperwepresentaparallelalgorithmCONNECTwhichdeterminestheconnectedcomponentsofanundirectedgraphwithnverticesintimeO(log2n)usingn2processors.
Next,wemodifythealgorithmtodemonstrateanobser-vationduetoF.
P.
PreparataandR.
L.
Probert,viz.
,n[n/lgn]processors1sufficetoachieveatimeboundofO(log2n).
Finally,weshowthatCONNECTcanbemodifiedtocomputethetransitiveclosureofannxnsymmetricBooleanmatrixintimeO(log2n)usingn[n/lgn]processors.
Weusethesingleinstructionstream-multipledatastream(SIMD)modelofparallelprocessors.
Itisassumedthattheprocessorshaveaccesstoacommonmemory,andthatsimultaneousaccesstothesamelocationispermittedforfetchinstructionsbutnotforstoreinstructions.
TheAlgorithmConnectWepresentaparallelalgorithmwhichusesn2processorstofindtheconnectedcomponentsofanundirectedgraphwithnverticesintimeO(log2n).
AnO0og2n)timeboundalsocanbeachievedusingonlyn[n/[log2n]]processors.
ThealgorithmcanheusedtofindthetransitiveclosureofasymmetricBooleanmatrix.
Weassumethattheprocessorshaveaccesstoacommonmemory.
Simultaneousaccesstothesamelocationispermittedforfetchinstructionsbutnotforstoreinstructions.
KeyWordsandPhrases:graphtheory,parallelprocessing,algorithms,transitiveclosure,connectedcomponentCRCategories:5.
25,5.
32,6.
22IntroductionParallelalgorithmsforsolvingvariouscomputationalproblemshavereceivedsubstantialattentionrecently,Permissiontocopywithoutfeeallorpartofthismaterialisgrantedprovidedthatthecopiesarenotmadeordistributedfordirectcommercialadvantage,theACMcopyrightnoticeandthetitleofthepublicationanditsdatoappear,andnoticeisgiventhatcopyingisbypermissionoftheAssociationforComputingMachinery.
Tocopyotherwise,ortorepublish,requiresafeeand/orspecificpermission.
TheworkofD.
S.
HirschbergwassupportedbytheNationalScienceFoundationunderGrantMCS-76-07683.
TheworkofD.
V.
SarwatewassupportedbytheJointServicesElectronicsProgramunderContractDAAG-29-78-C-0016.
Apreliminaryversionofthispaperwaspresentedatthe8thAnnualACMSymposiumontheTheoryofComputing,1976.
Authors'addresses:D.
S.
Hirschberg,DepartmentofElectricalEngineering,RiceUniversity,Houston,TX77001;A.
K.
Chandra,ComputerSciencesDepartment,IBMThomasJ.
WatsonResearchCenter,YorktownHeights,NY10598;D.
V.
Sarwate,CoordinatedScienceLaboratory,UniversityofIllinois,Urbana,IL61801.
1979ACM0001-0782/79/0800-0461$00.
75.
461LetV={0,1,2.
.
.
.
.
n-1),andletG=(V,E)denoteanundirectedgraphwithvertexsetVandedgesetE.
WerepresentGbyitsadjacencymatrixAwhichisannxnsymmetricBooleanmatrixwhereA(i,j)=1if(i,j)EEandA(i,j)=0otherwise.
Aconnectedcom-ponentofGisamaximalsubgraphofGsuchthatthereexistsapathbetweeneverypairofverticesinthesubgraph.
Eachvertexbelongstoexactlyoneconnectedcomponent,andweuseavectorDoflengthntospecifytheconnectedcomponentsofGasfollows.
IfGc--(Vc,Ec)isanyconnectedcomponent,thenforalliEV,,D(/)equalstheleastelementofV~.
TheparallelalgorithmCONNECTgivenbelowiterativelycomputesthevectorDfromtheadjacencymatrixAforanundi-rectedgraphonnvertices.
AlgorithmCONNECTInput:ThenXnadjacencymatrix.
4foranundirectedgraph.
Output:ThevectorDoflengthnsuchthatD(i)equalsthesmallest-numberedvertexintheconnectedcomponenttowhichibelongs.
Comment:Eachofthefollowingstepsisexecutedinparallelforalli,0__O,isadirectedgraphinwhicheveryvertexhasoutdegree1(i.
e.
exactlyoneedgeleaveseachvertex)andinwhichthereisexactlyonecycle,thelengthofthecyclebeingk+1.
Atree-loopisak-tree-loopforsomek.
Noticethatak-tree-loophasatleastk+1vertices.
Thereasonforthenametree-loopisthatifoneoftheedgesinthecycleisdeleted,weobtainarootedtree,therootbeingthevertexwithnoedgeleavingit.
Thedirec-tionofalltheedgesinthistreeisthereverseofthatgivenintheusualdefinition(seee.
g.
[1,p.
52]ofrootedtrees.
Weareinterestedinthesequelinl-tree-loops,whicharedefinedbythevectorCinthealgorithm,andinaspecialcaseof0-tree-loops(calledclubs)whicharedefinedbythevectorDinthealgorithm.
Definition.
Therootofa0-tree-loopisthevertexvsuchthattheedge(v,v)isthecycleoflength1.
Aclubisa0-tree-loopinwhichalltheedgesentertheroot.
LEMMA1.
LetGc=(Vc,Ec)denoteaconnectedcom-ponentofGsuchthatIVc[>-2anddefinethefunctionC:Vc---~VcbyC(i)=min(jlA[i,j]=1ANDj#i).
ThefunctionCdefinesadirectedgraphG~(C)=(Vc,E")whereE"={(i,C(i))[iEV~).
ThenG~(C)isacollectionofl-tree-loops,andthesmallest-numberedvertexineachtree-loopisinthecycleofthetree-loop.
PROOF.
FromthefactthatCisafunction,itiseasytoseethatGo(C)isacollectionoftree-loops.
SinceC(i)#i,noneofthetree-loopscanbea0-tree-loop.
Ifatree-loopinG~(C)isak-tree-loop,letVo,vl,v2.
.
.
.
.
vk,v0denotethesuccessiveverticesinthecycle(i.
e.
C(vi)-~-V/+lfori=0,1.
.
.
.
.
k-1andC(vk)=Vo)where,withoutlossofgenerality,v0=min{vo,vl.
.
.
.
.
vk).
How-ever,inthegraphG~,bothVoandv2areneighborsofvl.
HenceC(v~)=v2>Vowhichcontradictsthedefini-tionofCexceptwhenk=1.
Inthiscase,thetwoverticesintheloopareVoandvlwithC(vo)=v~andC(vl)=vo.
Asimilarargumentshowsthatthesmallest-numbered462vertexinthetree-loopmustbeinthecycleofthetree-loop.
[]LetusmaketheusualdefinitionofCk(v)asCl(v)=C(v)andCk(v)=C(Ck-l(v))fork>1.
LEMMA2.
LetCbedefinedasinLemma1andletvbeanyvertexinatree-loopofGo(C).
Letvoandvldenotethetwoverticesinthecycleofthetree-loop.
Then,forallN>_n-2,oneofthetwonumbersCN(v)andCN+I(v)equalsVoandtheotherequalsVx.
PROOF.
Theresultfollowseasilyfromthefactthatthepathfromvtothenearerofv0andvlisoflengthatmostn-2.
[]Thetwolemmasabovearethebasisofthemethodusedinthealgorithmtoidentifyverticesinthesameconnectedcomponent.
ThefunctionCsetsuptree-loopsineachconnectedcomponent,thefunctionCNiscom-putediteratively,andthenD(v)~--min{CN(v),CN+I(v)}setsupclubs(supervertices)withrootsv0.
Thereare,ofcourse,numerousbookkeepingdetailstobesettled,andwetakeuptheseintheproofofthefollowingtheorem.
THEOREM.
AlgorithmCONNECTcomputesthecon-nectedcomponentsoftheundirectedgraphGspecifiedbythesymmetricBooleanmatrixA.
PROOF.
Itiseasytoverifythatforthetrivialcon-nectedcomponentsconsistingofisolatedverticesLD(i)issettoiatstep1andremainsunchangedthroughouttheexecutionofthealgorithm.
Intheremainderofthisproof,weconsiderconnectedcomponentswithtwoormoreverticesonly.
LetG(D)=(V,ED)denotethedirectedgraphdefinedbyDwhereEo={(i,D(/))Ii~V}.
Aftertheexecutionofstep1,andjustpriortotheexecutionofstep2,G(D)satisfiesthefollowingproperties:(i)G(D)isasetofclubs(withdisjointvertexsets).
(ii)Therootofeachclubisthesmallest-numberedvertexintheclub.
(iii)Thevertexsetofanyclubisasubsetofthevertexsetofsomeconnectedcomponent.
WeshowthatifG(D)satisfiesproperties(i)-(iii)justpriortotheexecutionofstep2,thenafterexecutingsteps2-6,thenewfunctionD(computedatstep6)issuchthatthenewG(D)alsohasproperties(i)-(iii).
Furthermore,thenumbersofclubsineachconnectedcomponentisreducedbyafactorofatleast2,providedthattherewereatleasttwoclubsintheconnectedcomponentjustpriortostep2.
Itisinstructivetoobservewhathappensduringthefirstiterationofsteps2-6.
SinceDistheidentityfunc-tion,thefunctionCdefinedatstep2isexactlythefunctionofLemma1,andsetsup1-tree-loopsineachconnectedcomponentofG.
Step3doesnotchangeCbecausetheonlyjsatisfyingD(j)=iisiitself,andC(i)#i.
Instep4,thefunctionCiscopiedintoD,whileinstep5,CistransformedtoCNwhereN=2~g"_>n.
Step6setsD(i)tomin(CN(/),D(ClV(i))}whichisthesameasmin(C/V(i),cN+t(i)}.
ItfollowsfromLemma2thatforalli,D(i)equalsthesmallest-numberedvertexinCommunicationsAugust1979ofVolume22theACMNumber8thetree-loopthatcontainedi.
Thusthesetofverticesineachtree-loophasbeenmergedintoaclub.
Itiseasytoseethatafterthefirstiteration,G(D)satisfiesproperties(i)-(iii).
Sinceeach1-tree-loopcontainedatleasttwovertices,thenumberofclubsineachnontrivialcon-nectedcomponentisnomorethanhalfthenumberofvertices(dubs)thatitcontainedoriginally.
Asmentionedearlier,furtheriterationsofsteps2-6mergesupervertices,i.
e.
clubs.
Connectionsbetweensu-perverticesmaybedefinedasfollows.
LetVrdenotethesetofrootsofclubsinG(D)andletGr=(Vr,Er)denoteanundirectedgraphwherefori~j,(vi,vi)EErifandonlyifthereexistverticesv~andv~intheclubsofviandvj,respectively,suchthat(v~,v~~E.
Inotherwords,superverticesareneighborsifandonlyifthereisanedgeconnectingsomepairofmembervertices.
ThefunctionCissetupinsteps2and3.
Instep2,eachvertexiexaminestheclubmembershipsofitsneighborsandsetsC(i)tothesmallest-numberedneighboringclub.
Instep3,eachiEVrexaminesitsownclubmembers(specifiedbyD(j)=i)andpicksthesmallest-numberedofallthesmallest-numberedclubsthatthemembersfound.
Inshort,thefunctionC:Vr---)VrissuchthatforalliEVr,C(0equalsthesmallest-numberedvertexthatisadjacenttoiinGr.
AsinLemma1,Cdefinesacollectionofl-tree-loopsonGr.
Nextletusconsiderverticesi~Vr.
Forsuchvertices,thereisnojsuchthatD(j)=iandthusatstep3,C(/)isresettoD(/).
Hence,C:V~Vdefinesacollectionof1-tree-loopsonGbecauseeachnonrootispointingtoarootandtherootsarein1-tree-loops.
Itfollows(asinthediscussionofthefirstiterationofsteps2-6)thatafterstep6,thenewfunctionDissuchthatG(D)satisfiesproperties(i)-(iii).
Furthermore,each1-tree-loopinvolvestwoormoreverticesinGr,i.
e.
twoormoreclubs,andhenceineachconnectedcomponentthatcontainedatleasttwoclubs,thenumberofclubsisdecreasedbyafactorofatleast2.
Fromtheabovediscussion,itisclearthatthenumberofclubsineachconnectedcomponentdecreasesbyafactorofatleast2ateachiterationuntiltheconnectedcomponentconsistsofasingleclub.
Itiseasytoverifythatfurtheriterationsdonotaffectsuchsingleclubs.
Sincethereareatmostnvertices(clubs)tobeginwith,lgniterationssufficetoreduceeachconnectedcompo-nenttoasingleclub,whereclubmembershipisdefinedbyD.
[]WehaveshownthatCONNECTcomputesthecon-nectedcomponentsofthegraphGspecifiedbythesymmetricBooleanmatrixA.
ThetransitiveclosureofA,denotedbyA*,isgivenbyA*(i,j)=1ifandonlyifthereisapathinGfromitoj,i.
e.
ifandonlyifiandjareinthesameconnectedcomponent.
HenceweobtainanalgorithmforthetransitiveclosureofsymmetricmatricesbyaddingthefollowingsteptoCONNECT:7.
foralli,jfloifD(0=D(j)thenA*(i,j)~1andbychangingtheinput-outputspecificationsappro-priately.
463TimeandProcessorBoundsThemainloopoftheprogramisexecutedlgntimes,whilewithintheloop,theiterationatstep5isexecutedlgntimes.
Thusthealgorithmrequires~(log2n)timeregardlessofthenumberofprocessorsused.
Letussupposethatn2processorsareavailable.
Steps1,4,and6requireonlyO(1)timewhenever~(n)processorsareavailable,whilestep5requiresO(logn)timewiththesameprocessorrequirements.
Wenowshowthatsteps2and3alsocanbeprogrammedtoexecuteintimeO(logn)togiveanO(log2n)timeboundusingn2proc-essors.
Theprogramforstep2isStep2.
Thefollowingstepsareperformedinparallelfor0_2(a)Foralli,jdoifA(i,j)=1ANDO(j)#D(i)thenTemp(i,j)~--D(j)elseTemp(i,j)~--on2(b)Fork~--0until(lgn)-1doforalli,jdoTemp(i,j)min{Temp(i,j),Temp(i,j+2*modn)}2(c)ForallidoifTemp(i,0)=~thenC(i)~D(i)elseC(i)~Temp(i,O)Hereonmeansanynumberexceedingn-1.
Instep2(a)thenumberswhoseminimumistobecomputedarestoredinthearrayTemp.
Instep2(b),theminimumisfoundasfollows.
AtthefirstiterationTemp(i,0)iscomparedwithTemp(i,1)asisTemp(i,2)withTemp(i,3),Temp(i,4)withTemp(i,5).
.
.
etc.
Attheseconditeration,Temp(i,0)iscomparedwithTemp(i,2),Temp(i,4)withTemp(i,6)etc.
Theformercomparisonfindsmin(Temp(i,j),0<_j<--3},whilethelatterfindsmin{Temp(i,j),4<_j<_7)etc.
Thus,inlgniterationstheminimumisfound.
Themethodissimplebutwaste-fulofprocessorsinthat,forexample,theresultofcomparingTemp(i,1)withTemp(i,2)isnotusedatall.
Obviously,foreachvalueofi,[n/2]processorswouldsufficeforthefirstiteration,[[n/2]/2]forthesecondetc.
Theprogramforstep3issimilarandwillnotbestatedseparately.
Thenetresultisthefollowingtheorem.
THEOREM.
AlgorithmCONNECTfindstheconnectedcomponentsofanundirectedgraphwithnverticesintimeO(log2n)usingn2processors.
COROLLARY.
Thetransitiveclosureofann*nsym-metricBooleanmatrixcanbefoundintimeO(log2n)usingnzprocessors.
ThereductioninthenumberofprocessorsthatwasobservedbyPreparataandProbertoccursasfollows.
Wepartitiontheintegers{0___jEachsuchsubset(exceptpossiblytheonewithk=[n/lgn]-1)haslgnelements.
Theideaistocomputethen2entriesofthearr~iyTempintimeO(logn)usingn[n/lgn]processors.
InordertocomputetheminimumvalueofTemp(i,j)for0_ThesearefoundintimeCommunicationsAugust1979ofVolume22theACMNumber8O(logn)viasequentialsearch.
Then,theminimumofthe[n/lgn]candidateminimaisfound(asinstep2(b)above)intimeO(logn-loglogn)using[n/lgn]processorsateachstep.
Thegrubbydetailsareasfollows.
Step2.
Thefollowingstepsareperformedinparallelfor0_2(a)ForI,,-0until(lgn)-1doforalli,kdoifA(i,l+klgn)=1ANDD(i)~D(I+klgn)thenTemp(i,1+klgn)*--D(I+klgn)elseTemp(i,l+klgn)~2(b)Forl~luntil(lgn)-1doforalli,kdoTemp(i,kIgn)~min{Temp(i,klgn),Temp(i,l+klgn)}2(c)For1~--0until(lgrn/lgn'D-1doforalli,kdoTemp(Lklgn)~min{Temp(i,klgn),Temp(i,(k+2t)lgnmodn)}2(d)ForallidoifTemp(i,0)=oothenC(i)*--D(i)elseC(i)~Temp(i,O)Intheaboveprogram,wehaveignoredthefactthatoneofthe[n/lgn]subsetsmaycontainfewerthanlgnelements.
Onewayaroundthisistopadthearrays,4,C,andDapproximately.
Anotherpossibilityistoreplacel+klgnby(l+klgn)modn.
Theprogramforstep3issimilarandwehavethefollowingtheorem.
THEOREM.
AlgorithmCONNECTfindstheconnectedcomponentsofanundirectedgraphwithnverticesintimeO(log2n)usingnrn/lgn]processors.
COROLLARY.
ThetransitiveclosureofannXnsym-metricBooleanmatrixcanbefoundintimeO(log2n)usingn[n/lgn]processors.
Remark.
In[5],itisshownthatthetransitiveclosureofanarbitrarynxnBooleanmatrixcanbefoundintimeO(log2n)usingO(nl°g27/logn)processors.
AlthoughtheexponentofnmaybereducedslightlybyusingsomerecentresultsofPan[11],itisclearthatsymmetryreducesprocessorrequirementssignificantlyforthetran-sitiveclosureproblem.
7.
Hirschberg,D.
S.
Fastparallelsortingalgorithms.
Comm.
ACM21,8(Aug.
1978),657-661.
8.
Hyafil,L.
,andKung,H.
T.
Thecomplexityofparallelevaluationoflinearrecurrences.
J.
ACM24,(July1977),513-521.
9.
Levitt,K.
N.
,andKautz,W.
H.
Cellulararraysforthesolutionofgraphproblems.
Comm.
ACM15,(Sept.
1972),789-801.
10.
Munro,I.
,]ndPaterson,M.
Optimalalgorithmsforparallelpolynomialevaluation.
J.
Comp.
Syst.
Sci.
7(1973),183-198.
11.
Pan,V.
Y.
Strassen'salgorithmisnotoptimal.
Proc.
19thAnnu.
Symp.
onFoundationsofComptr.
Sci.
,1978,pp.
166-176.
12.
Preparata,F.
P.
Newparallel-sortingschemes.
IEEETrans.
Comptrs.
C-27(July1978),669-673.
13.
Preparata,F.
P.
,andSarwate,D.
V.
Animprovedparallelprocessorboundinfastmatrixinversion.
Inf.
Proc.
Letters7(April1978),148-150.
14.
Reghbati,E.
,andCorneil,D.
C.
Parallelcomputationsingraphtheory.
SlAMJ.
Comping.
7(May1978),230-237.
15.
Savage,C.
D.
Parallelalgorithmsforgraphtheoreticproblems.
Ph.
D.
Th.
,U.
ofIllinois,Urbana,I11.
,Aug.
1977.
16.
Thompson,C.
D.
,andKung,H.
T.
Sortingonamesh-connectedparallelcomputer.
Comm.
ACM20,4(April1977),263-271.
ReceivedOctober1975;revisedOctober1978References1.
Aho,AN.
,Hopcroft,J.
E.
,andUllman,J.
D.
TheDesignandAnalysisofComputerAlgorithms,Addison-Wesley,Reading,Mass.
,1974.
2.
Batcher,K.
E.
Sortingnetworksandtheirapplications.
Proc.
AFIPS1968SJCC,Vol.
32,AFIPSPress,Montvale,N.
J.
,pp.
307-314.
3.
Baudet,G.
,andStevenson,D.
Optimalsortingalgorithmsforparallelcomputers.
1EEETrans.
Comptrs.
C-27(Jan.
1978),84-87.
4.
Brent,R.
P.
Theparallelevaluationofgeneralarithmeticexpressions.
J.
ACM21,(April1974),201-206.
5.
Chandra,A.
K.
Maximalparallelisminmatrixmultiplication.
~BMTech.
Rep.
RC6193,Sept.
1976.
6.
Csanky,L.
Fastparallelmatrixinversionalgorithms,SlAMJ.
Comping.
5(Dec.
1976),618-623.
464CommunicationsAugust1979ofVolume22theACMNumber8
K.
ManacherTechniquesEditorComputingConnectedComponentsonParallelComputersD.
S.
HirschbergRiceUniversityA.
K.
ChandraIBMThomasJ.
WatsonResearchCenterD.
V.
SarwateUniversityofIllinoismotivatedinpartbypracticalconsiderations.
Amongthemanyareastreatedintherecentliteraturearesorting[2,3,7,12,15],theevaluationofarithmeticexpressions,linearrecurrencesandpolynomials[4,8,10],matrixalgorithms[5,6,13],andgraphtheory[9,14,15].
InthispaperwepresentaparallelalgorithmCONNECTwhichdeterminestheconnectedcomponentsofanundirectedgraphwithnverticesintimeO(log2n)usingn2processors.
Next,wemodifythealgorithmtodemonstrateanobser-vationduetoF.
P.
PreparataandR.
L.
Probert,viz.
,n[n/lgn]processors1sufficetoachieveatimeboundofO(log2n).
Finally,weshowthatCONNECTcanbemodifiedtocomputethetransitiveclosureofannxnsymmetricBooleanmatrixintimeO(log2n)usingn[n/lgn]processors.
Weusethesingleinstructionstream-multipledatastream(SIMD)modelofparallelprocessors.
Itisassumedthattheprocessorshaveaccesstoacommonmemory,andthatsimultaneousaccesstothesamelocationispermittedforfetchinstructionsbutnotforstoreinstructions.
TheAlgorithmConnectWepresentaparallelalgorithmwhichusesn2processorstofindtheconnectedcomponentsofanundirectedgraphwithnverticesintimeO(log2n).
AnO0og2n)timeboundalsocanbeachievedusingonlyn[n/[log2n]]processors.
ThealgorithmcanheusedtofindthetransitiveclosureofasymmetricBooleanmatrix.
Weassumethattheprocessorshaveaccesstoacommonmemory.
Simultaneousaccesstothesamelocationispermittedforfetchinstructionsbutnotforstoreinstructions.
KeyWordsandPhrases:graphtheory,parallelprocessing,algorithms,transitiveclosure,connectedcomponentCRCategories:5.
25,5.
32,6.
22IntroductionParallelalgorithmsforsolvingvariouscomputationalproblemshavereceivedsubstantialattentionrecently,Permissiontocopywithoutfeeallorpartofthismaterialisgrantedprovidedthatthecopiesarenotmadeordistributedfordirectcommercialadvantage,theACMcopyrightnoticeandthetitleofthepublicationanditsdatoappear,andnoticeisgiventhatcopyingisbypermissionoftheAssociationforComputingMachinery.
Tocopyotherwise,ortorepublish,requiresafeeand/orspecificpermission.
TheworkofD.
S.
HirschbergwassupportedbytheNationalScienceFoundationunderGrantMCS-76-07683.
TheworkofD.
V.
SarwatewassupportedbytheJointServicesElectronicsProgramunderContractDAAG-29-78-C-0016.
Apreliminaryversionofthispaperwaspresentedatthe8thAnnualACMSymposiumontheTheoryofComputing,1976.
Authors'addresses:D.
S.
Hirschberg,DepartmentofElectricalEngineering,RiceUniversity,Houston,TX77001;A.
K.
Chandra,ComputerSciencesDepartment,IBMThomasJ.
WatsonResearchCenter,YorktownHeights,NY10598;D.
V.
Sarwate,CoordinatedScienceLaboratory,UniversityofIllinois,Urbana,IL61801.
1979ACM0001-0782/79/0800-0461$00.
75.
461LetV={0,1,2.
.
.
.
.
n-1),andletG=(V,E)denoteanundirectedgraphwithvertexsetVandedgesetE.
WerepresentGbyitsadjacencymatrixAwhichisannxnsymmetricBooleanmatrixwhereA(i,j)=1if(i,j)EEandA(i,j)=0otherwise.
Aconnectedcom-ponentofGisamaximalsubgraphofGsuchthatthereexistsapathbetweeneverypairofverticesinthesubgraph.
Eachvertexbelongstoexactlyoneconnectedcomponent,andweuseavectorDoflengthntospecifytheconnectedcomponentsofGasfollows.
IfGc--(Vc,Ec)isanyconnectedcomponent,thenforalliEV,,D(/)equalstheleastelementofV~.
TheparallelalgorithmCONNECTgivenbelowiterativelycomputesthevectorDfromtheadjacencymatrixAforanundi-rectedgraphonnvertices.
AlgorithmCONNECTInput:ThenXnadjacencymatrix.
4foranundirectedgraph.
Output:ThevectorDoflengthnsuchthatD(i)equalsthesmallest-numberedvertexintheconnectedcomponenttowhichibelongs.
Comment:Eachofthefollowingstepsisexecutedinparallelforalli,0__O,isadirectedgraphinwhicheveryvertexhasoutdegree1(i.
e.
exactlyoneedgeleaveseachvertex)andinwhichthereisexactlyonecycle,thelengthofthecyclebeingk+1.
Atree-loopisak-tree-loopforsomek.
Noticethatak-tree-loophasatleastk+1vertices.
Thereasonforthenametree-loopisthatifoneoftheedgesinthecycleisdeleted,weobtainarootedtree,therootbeingthevertexwithnoedgeleavingit.
Thedirec-tionofalltheedgesinthistreeisthereverseofthatgivenintheusualdefinition(seee.
g.
[1,p.
52]ofrootedtrees.
Weareinterestedinthesequelinl-tree-loops,whicharedefinedbythevectorCinthealgorithm,andinaspecialcaseof0-tree-loops(calledclubs)whicharedefinedbythevectorDinthealgorithm.
Definition.
Therootofa0-tree-loopisthevertexvsuchthattheedge(v,v)isthecycleoflength1.
Aclubisa0-tree-loopinwhichalltheedgesentertheroot.
LEMMA1.
LetGc=(Vc,Ec)denoteaconnectedcom-ponentofGsuchthatIVc[>-2anddefinethefunctionC:Vc---~VcbyC(i)=min(jlA[i,j]=1ANDj#i).
ThefunctionCdefinesadirectedgraphG~(C)=(Vc,E")whereE"={(i,C(i))[iEV~).
ThenG~(C)isacollectionofl-tree-loops,andthesmallest-numberedvertexineachtree-loopisinthecycleofthetree-loop.
PROOF.
FromthefactthatCisafunction,itiseasytoseethatGo(C)isacollectionoftree-loops.
SinceC(i)#i,noneofthetree-loopscanbea0-tree-loop.
Ifatree-loopinG~(C)isak-tree-loop,letVo,vl,v2.
.
.
.
.
vk,v0denotethesuccessiveverticesinthecycle(i.
e.
C(vi)-~-V/+lfori=0,1.
.
.
.
.
k-1andC(vk)=Vo)where,withoutlossofgenerality,v0=min{vo,vl.
.
.
.
.
vk).
How-ever,inthegraphG~,bothVoandv2areneighborsofvl.
HenceC(v~)=v2>Vowhichcontradictsthedefini-tionofCexceptwhenk=1.
Inthiscase,thetwoverticesintheloopareVoandvlwithC(vo)=v~andC(vl)=vo.
Asimilarargumentshowsthatthesmallest-numbered462vertexinthetree-loopmustbeinthecycleofthetree-loop.
[]LetusmaketheusualdefinitionofCk(v)asCl(v)=C(v)andCk(v)=C(Ck-l(v))fork>1.
LEMMA2.
LetCbedefinedasinLemma1andletvbeanyvertexinatree-loopofGo(C).
Letvoandvldenotethetwoverticesinthecycleofthetree-loop.
Then,forallN>_n-2,oneofthetwonumbersCN(v)andCN+I(v)equalsVoandtheotherequalsVx.
PROOF.
Theresultfollowseasilyfromthefactthatthepathfromvtothenearerofv0andvlisoflengthatmostn-2.
[]Thetwolemmasabovearethebasisofthemethodusedinthealgorithmtoidentifyverticesinthesameconnectedcomponent.
ThefunctionCsetsuptree-loopsineachconnectedcomponent,thefunctionCNiscom-putediteratively,andthenD(v)~--min{CN(v),CN+I(v)}setsupclubs(supervertices)withrootsv0.
Thereare,ofcourse,numerousbookkeepingdetailstobesettled,andwetakeuptheseintheproofofthefollowingtheorem.
THEOREM.
AlgorithmCONNECTcomputesthecon-nectedcomponentsoftheundirectedgraphGspecifiedbythesymmetricBooleanmatrixA.
PROOF.
Itiseasytoverifythatforthetrivialcon-nectedcomponentsconsistingofisolatedverticesLD(i)issettoiatstep1andremainsunchangedthroughouttheexecutionofthealgorithm.
Intheremainderofthisproof,weconsiderconnectedcomponentswithtwoormoreverticesonly.
LetG(D)=(V,ED)denotethedirectedgraphdefinedbyDwhereEo={(i,D(/))Ii~V}.
Aftertheexecutionofstep1,andjustpriortotheexecutionofstep2,G(D)satisfiesthefollowingproperties:(i)G(D)isasetofclubs(withdisjointvertexsets).
(ii)Therootofeachclubisthesmallest-numberedvertexintheclub.
(iii)Thevertexsetofanyclubisasubsetofthevertexsetofsomeconnectedcomponent.
WeshowthatifG(D)satisfiesproperties(i)-(iii)justpriortotheexecutionofstep2,thenafterexecutingsteps2-6,thenewfunctionD(computedatstep6)issuchthatthenewG(D)alsohasproperties(i)-(iii).
Furthermore,thenumbersofclubsineachconnectedcomponentisreducedbyafactorofatleast2,providedthattherewereatleasttwoclubsintheconnectedcomponentjustpriortostep2.
Itisinstructivetoobservewhathappensduringthefirstiterationofsteps2-6.
SinceDistheidentityfunc-tion,thefunctionCdefinedatstep2isexactlythefunctionofLemma1,andsetsup1-tree-loopsineachconnectedcomponentofG.
Step3doesnotchangeCbecausetheonlyjsatisfyingD(j)=iisiitself,andC(i)#i.
Instep4,thefunctionCiscopiedintoD,whileinstep5,CistransformedtoCNwhereN=2~g"_>n.
Step6setsD(i)tomin(CN(/),D(ClV(i))}whichisthesameasmin(C/V(i),cN+t(i)}.
ItfollowsfromLemma2thatforalli,D(i)equalsthesmallest-numberedvertexinCommunicationsAugust1979ofVolume22theACMNumber8thetree-loopthatcontainedi.
Thusthesetofverticesineachtree-loophasbeenmergedintoaclub.
Itiseasytoseethatafterthefirstiteration,G(D)satisfiesproperties(i)-(iii).
Sinceeach1-tree-loopcontainedatleasttwovertices,thenumberofclubsineachnontrivialcon-nectedcomponentisnomorethanhalfthenumberofvertices(dubs)thatitcontainedoriginally.
Asmentionedearlier,furtheriterationsofsteps2-6mergesupervertices,i.
e.
clubs.
Connectionsbetweensu-perverticesmaybedefinedasfollows.
LetVrdenotethesetofrootsofclubsinG(D)andletGr=(Vr,Er)denoteanundirectedgraphwherefori~j,(vi,vi)EErifandonlyifthereexistverticesv~andv~intheclubsofviandvj,respectively,suchthat(v~,v~~E.
Inotherwords,superverticesareneighborsifandonlyifthereisanedgeconnectingsomepairofmembervertices.
ThefunctionCissetupinsteps2and3.
Instep2,eachvertexiexaminestheclubmembershipsofitsneighborsandsetsC(i)tothesmallest-numberedneighboringclub.
Instep3,eachiEVrexaminesitsownclubmembers(specifiedbyD(j)=i)andpicksthesmallest-numberedofallthesmallest-numberedclubsthatthemembersfound.
Inshort,thefunctionC:Vr---)VrissuchthatforalliEVr,C(0equalsthesmallest-numberedvertexthatisadjacenttoiinGr.
AsinLemma1,Cdefinesacollectionofl-tree-loopsonGr.
Nextletusconsiderverticesi~Vr.
Forsuchvertices,thereisnojsuchthatD(j)=iandthusatstep3,C(/)isresettoD(/).
Hence,C:V~Vdefinesacollectionof1-tree-loopsonGbecauseeachnonrootispointingtoarootandtherootsarein1-tree-loops.
Itfollows(asinthediscussionofthefirstiterationofsteps2-6)thatafterstep6,thenewfunctionDissuchthatG(D)satisfiesproperties(i)-(iii).
Furthermore,each1-tree-loopinvolvestwoormoreverticesinGr,i.
e.
twoormoreclubs,andhenceineachconnectedcomponentthatcontainedatleasttwoclubs,thenumberofclubsisdecreasedbyafactorofatleast2.
Fromtheabovediscussion,itisclearthatthenumberofclubsineachconnectedcomponentdecreasesbyafactorofatleast2ateachiterationuntiltheconnectedcomponentconsistsofasingleclub.
Itiseasytoverifythatfurtheriterationsdonotaffectsuchsingleclubs.
Sincethereareatmostnvertices(clubs)tobeginwith,lgniterationssufficetoreduceeachconnectedcompo-nenttoasingleclub,whereclubmembershipisdefinedbyD.
[]WehaveshownthatCONNECTcomputesthecon-nectedcomponentsofthegraphGspecifiedbythesymmetricBooleanmatrixA.
ThetransitiveclosureofA,denotedbyA*,isgivenbyA*(i,j)=1ifandonlyifthereisapathinGfromitoj,i.
e.
ifandonlyifiandjareinthesameconnectedcomponent.
HenceweobtainanalgorithmforthetransitiveclosureofsymmetricmatricesbyaddingthefollowingsteptoCONNECT:7.
foralli,jfloifD(0=D(j)thenA*(i,j)~1andbychangingtheinput-outputspecificationsappro-priately.
463TimeandProcessorBoundsThemainloopoftheprogramisexecutedlgntimes,whilewithintheloop,theiterationatstep5isexecutedlgntimes.
Thusthealgorithmrequires~(log2n)timeregardlessofthenumberofprocessorsused.
Letussupposethatn2processorsareavailable.
Steps1,4,and6requireonlyO(1)timewhenever~(n)processorsareavailable,whilestep5requiresO(logn)timewiththesameprocessorrequirements.
Wenowshowthatsteps2and3alsocanbeprogrammedtoexecuteintimeO(logn)togiveanO(log2n)timeboundusingn2proc-essors.
Theprogramforstep2isStep2.
Thefollowingstepsareperformedinparallelfor0_
Instep2(a)thenumberswhoseminimumistobecomputedarestoredinthearrayTemp.
Instep2(b),theminimumisfoundasfollows.
AtthefirstiterationTemp(i,0)iscomparedwithTemp(i,1)asisTemp(i,2)withTemp(i,3),Temp(i,4)withTemp(i,5).
.
.
etc.
Attheseconditeration,Temp(i,0)iscomparedwithTemp(i,2),Temp(i,4)withTemp(i,6)etc.
Theformercomparisonfindsmin(Temp(i,j),0<_j<--3},whilethelatterfindsmin{Temp(i,j),4<_j<_7)etc.
Thus,inlgniterationstheminimumisfound.
Themethodissimplebutwaste-fulofprocessorsinthat,forexample,theresultofcomparingTemp(i,1)withTemp(i,2)isnotusedatall.
Obviously,foreachvalueofi,[n/2]processorswouldsufficeforthefirstiteration,[[n/2]/2]forthesecondetc.
Theprogramforstep3issimilarandwillnotbestatedseparately.
Thenetresultisthefollowingtheorem.
THEOREM.
AlgorithmCONNECTfindstheconnectedcomponentsofanundirectedgraphwithnverticesintimeO(log2n)usingn2processors.
COROLLARY.
Thetransitiveclosureofann*nsym-metricBooleanmatrixcanbefoundintimeO(log2n)usingnzprocessors.
ThereductioninthenumberofprocessorsthatwasobservedbyPreparataandProbertoccursasfollows.
Wepartitiontheintegers{0___j
Theideaistocomputethen2entriesofthearr~iyTempintimeO(logn)usingn[n/lgn]processors.
InordertocomputetheminimumvalueofTemp(i,j)for0_
Then,theminimumofthe[n/lgn]candidateminimaisfound(asinstep2(b)above)intimeO(logn-loglogn)using[n/lgn]processorsateachstep.
Thegrubbydetailsareasfollows.
Step2.
Thefollowingstepsareperformedinparallelfor0_
Onewayaroundthisistopadthearrays,4,C,andDapproximately.
Anotherpossibilityistoreplacel+klgnby(l+klgn)modn.
Theprogramforstep3issimilarandwehavethefollowingtheorem.
THEOREM.
AlgorithmCONNECTfindstheconnectedcomponentsofanundirectedgraphwithnverticesintimeO(log2n)usingnrn/lgn]processors.
COROLLARY.
ThetransitiveclosureofannXnsym-metricBooleanmatrixcanbefoundintimeO(log2n)usingn[n/lgn]processors.
Remark.
In[5],itisshownthatthetransitiveclosureofanarbitrarynxnBooleanmatrixcanbefoundintimeO(log2n)usingO(nl°g27/logn)processors.
AlthoughtheexponentofnmaybereducedslightlybyusingsomerecentresultsofPan[11],itisclearthatsymmetryreducesprocessorrequirementssignificantlyforthetran-sitiveclosureproblem.
7.
Hirschberg,D.
S.
Fastparallelsortingalgorithms.
Comm.
ACM21,8(Aug.
1978),657-661.
8.
Hyafil,L.
,andKung,H.
T.
Thecomplexityofparallelevaluationoflinearrecurrences.
J.
ACM24,(July1977),513-521.
9.
Levitt,K.
N.
,andKautz,W.
H.
Cellulararraysforthesolutionofgraphproblems.
Comm.
ACM15,(Sept.
1972),789-801.
10.
Munro,I.
,]ndPaterson,M.
Optimalalgorithmsforparallelpolynomialevaluation.
J.
Comp.
Syst.
Sci.
7(1973),183-198.
11.
Pan,V.
Y.
Strassen'salgorithmisnotoptimal.
Proc.
19thAnnu.
Symp.
onFoundationsofComptr.
Sci.
,1978,pp.
166-176.
12.
Preparata,F.
P.
Newparallel-sortingschemes.
IEEETrans.
Comptrs.
C-27(July1978),669-673.
13.
Preparata,F.
P.
,andSarwate,D.
V.
Animprovedparallelprocessorboundinfastmatrixinversion.
Inf.
Proc.
Letters7(April1978),148-150.
14.
Reghbati,E.
,andCorneil,D.
C.
Parallelcomputationsingraphtheory.
SlAMJ.
Comping.
7(May1978),230-237.
15.
Savage,C.
D.
Parallelalgorithmsforgraphtheoreticproblems.
Ph.
D.
Th.
,U.
ofIllinois,Urbana,I11.
,Aug.
1977.
16.
Thompson,C.
D.
,andKung,H.
T.
Sortingonamesh-connectedparallelcomputer.
Comm.
ACM20,4(April1977),263-271.
ReceivedOctober1975;revisedOctober1978References1.
Aho,AN.
,Hopcroft,J.
E.
,andUllman,J.
D.
TheDesignandAnalysisofComputerAlgorithms,Addison-Wesley,Reading,Mass.
,1974.
2.
Batcher,K.
E.
Sortingnetworksandtheirapplications.
Proc.
AFIPS1968SJCC,Vol.
32,AFIPSPress,Montvale,N.
J.
,pp.
307-314.
3.
Baudet,G.
,andStevenson,D.
Optimalsortingalgorithmsforparallelcomputers.
1EEETrans.
Comptrs.
C-27(Jan.
1978),84-87.
4.
Brent,R.
P.
Theparallelevaluationofgeneralarithmeticexpressions.
J.
ACM21,(April1974),201-206.
5.
Chandra,A.
K.
Maximalparallelisminmatrixmultiplication.
~BMTech.
Rep.
RC6193,Sept.
1976.
6.
Csanky,L.
Fastparallelmatrixinversionalgorithms,SlAMJ.
Comping.
5(Dec.
1976),618-623.
464CommunicationsAugust1979ofVolume22theACMNumber8
- rected27eee.com相关文档
- business27eee.com
- coordinates27eee.com
- 器件27eee.com
- generalized27eee.com
- 振荡器27eee.com
- Compliance27eee.com
VoLLcloud6折限量,香港CMI云服务器三网直连-200M带宽
vollcloud LLC首次推出6折促销,本次促销福利主要感恩与回馈广大用户对于我们的信任与支持,我们将继续稳步前行,为广大用户们提供更好的产品和服务,另外,本次促销码共限制使用30个,个人不限购,用完活动结束,同时所有vps产品支持3日内无条件退款和提供免费试用。需要了解更多产品可前往官网查看!vollcloud优惠码:VoLLcloud终生6折促销码:Y5C0V7R0YW商品名称CPU内存S...
bgpto:独立服务器夏季促销,日本机器6.5折、新加坡7.5折,20M带宽,低至$93/月
bgp.to对日本机房、新加坡机房的独立服务器在搞特价促销,日本独立服务器低至6.5折优惠,新加坡独立服务器低至7.5折优惠,所有优惠都是循环的,终身不涨价。服务器不限制流量,支持升级带宽,免费支持Linux和Windows server中文版(还包括Windows 10). 特色:自动部署,无需人工干预,用户可以在后台自己重装系统、重启、关机等操作!官方网站:https://www.bgp.to...

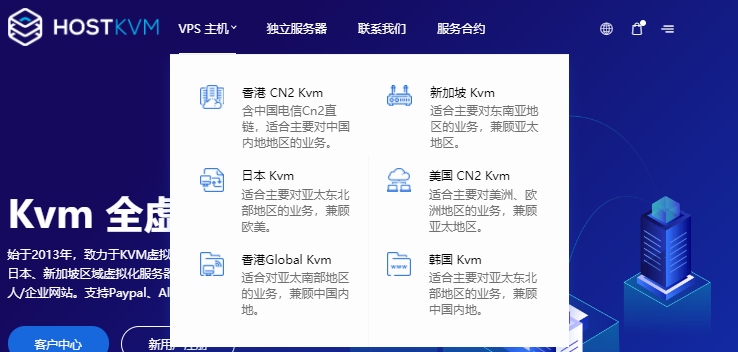
HostKvm四月优惠:VPS主机全场八折,香港/美国洛杉矶机房$5.2/月起
HostKvm是一家成立于2013年的国外主机服务商,主要提供基于KVM架构的VPS主机,可选数据中心包括日本、新加坡、韩国、美国、中国香港等多个地区机房,均为国内直连或优化线路,延迟较低,适合建站或者远程办公等。本月商家针对全场VPS主机提供8折优惠码,优惠后美国洛杉矶VPS月付5.2美元起。下面列出几款不同机房VPS主机产品配置信息。套餐:美国US-Plan0CPU:1cores内存:1GB硬...
27eee.com为你推荐
-
百度关键词工具常见百度关键词挖掘方法分别是什么请列举?www.e12.com.cn上海高中除了四大名校,接下来哪所高中最好?顺便讲下它的各方面情况mole.61.com谁知道摩尔庄园的网址啊125xx.com115xx.com是什么意思www.zjs.com.cn请问宅急送客服电话号码是多少?lcoc.toptop weenie 是什么?dadi.tv1223tv影院首页地址是什么?1223tv影院在哪里可以找到?dadi.tvApple TV是干嘛的?怎么用?多少钱?关键词分析怎么样分析关键词?邯郸纠风网邯郸媒体曝光电话多少