ostringstream#include<sstream.h>是什么作用
ostringstream 时间:2021-05-30 阅读:()
希尔排序的C++程序
// all_sort.cpp : Defines the entry point for the console application. // #include "stdafx.h" #include <iostream> #include <climits> #include <ctime> using namespace std; template<class T> void DirectSort1(T arr[],int n) //直接插入排序 { //元素从1开始存储,n表示数组中含有元素个数,此处即为最后一个元素的下标 for(int i=2;i<=n;i++) { if(arr[i]<arr[i-1]) { arr[0]=arr[i]; //设置监视哨 int j; for(j=i-1;arr[0]<arr[j];j--) arr[j+1]=arr[j]; arr[j+1]=arr[0]; } } } template<class T> void DirectSort2(T arr[],int left,int right) { //数组存储从0开始,不设置监视哨,left,right分别代表数组第一后最后一个元素的下标 for(int i=left+1;i<=right;i++) if(arr[i]<arr[i-1]) //当且仅当待排序元素比前面非递减有序序列最后一个元素小时才进行比较移动操作 { int j=i-1; T temp=arr[i]; do{ arr[j+1]=arr[j]; j--; }while(j>=left && arr[j]>temp); arr[j+1]=temp; } } template<class T> void BinInsertSort(T arr[],int n) //折半排序 { for(int i=2;i<=n;i++) { arr[0]=arr[i]; //设置监视哨 int low=1,high=i-1; //设置上下限 while(low<=high) //折半定位到插入位置 { int mid=(low+high)/2; if(arr[0]<arr[mid]) high=mid-1; else low=mid+1; } for(int j=i-1;j>=high+1;j--) arr[j+1]=arr[j]; //循环后移 arr[high+1]=arr[0]; //插入到定位位置 } } template<class T> struct Node { T data; int next; }; template<class T> void LinkDirSort(Node<T> arr[],int n) //链表实现直接插入排序——减少移动次数 { arr[0].data=INT_MAX; arr[0].next=1; arr[1].next=0; //元素从1开始存储,n表示数组中含有元素个数——此处即为最后一个元素的下标 for(int i=2;i<=n;i++) { int j,k; for(j=0,k=arr[0].next;arr[k].data<=arr[i].data;j=k,k=arr[k].next) ; arr[j].next=i; arr[i].next=k; } } template<class T> void ShellInsert(T arr[],int n,int dk) //n为元素个数,dk为增量 { for(int i=dk+1;i<=n;i++) //当dk==1时为直接插入排序,希尔排序可以减少直接插入排序的比较和移动次数 { if(arr[i]<arr[i-dk]) { arr[0]=arr[i]; //设置监视哨 int j; for(j=i-dk;j>0&&arr[0]<arr[j];j-=dk) //注意这里要确保j>0 arr[j+dk]=arr[j]; arr[j+dk]=arr[0]; } } } template<class T> void ShellSort(T arr[],int n) //希尔排序可形象比喻为:先进行大范围调节在进行小范围调节 { int dk=n/2; for(;dk>=1;dk/=2) //依次减小增量,当增量较少为1时进行直接插入排序(小调节) ShellInsert(arr,n,dk); //希尔插入 } template<class T> void BubbleSort(T arr[],int n) //冒泡排序 { //这里可以不像前面一样设置监视哨,元素直接从0开始,n仍然表示元素个数 //由小到大排序 for(int i=n;i>1;i--) //进行n-1趟排序 for(int j=0;j<i-1;j++) if(arr[j]>arr[j+1]) //如果相邻元素前面的比后面的大则进行冒泡 swap(arr[j],arr[j+1]); } template<class T> void SelectionSort(T arr[],int n) { //元素直接从0开始,n仍然表示元素个数,由小到大排序 for(int i=0;i<n-1;i++) //进行n-1趟排序 { int k=i; //设定待比元素 for(int j=i+1;j<n;j++) //j从待比元素后一个位置开始 if(arr[k]>arr[j]) //如果待比元素比后面元素大,将k指向小的元素 k=j; swap(arr[i],arr[k]); //将最小元素放在指定位置,这里可以不进行i!=k比较 } } //快速排序的不同实现 template<class T> int Partition1(T arr[],int low,int high) { int i=low,j=high-1; T pivot=arr[high]; //这里我们是把基准选在末端 for(;i<j;) //i<j判断不能取等号,当出现i==j时说明i j指向的元素都等于pivot,此时可以定位pivot了 { while( arr[i]<pivot) i++; //不能把i<j 判断放在下面两个循环控制中,而在for中不出现,如这样做:当最后一个元素最大时,函数却返回high-1 这肯定错 while( arr[j]>pivot) j--; if(i<j) { swap(arr[i],arr[j]); i++;j--; } else break; } if(arr[i]>pivot) //流程回到这里说明arr[i]>=pivot,当然arr[i]==pivot时没必要交换 { arr[high]=arr[i]; arr[i]=pivot; } return i; } template<class T> void QuickSort1(T arr[],int left,int right) { if(left<right) { int pos=Partition1(arr,left,right); QuickSort1(arr,left,pos-1); QuickSort1(arr,pos+1,right); } } template<class T> int Partition2(T arr[],int low,int high) { int pivotpos=low; T pivot=arr[low]; for(int i=low+1;i<=high;i++) { if(arr[i]<pivot) { pivotpos++; if(pivotpos!=i) swap(arr[pivotpos],arr[i]); } } arr[low]=arr[pivotpos]; arr[pivotpos]=pivot; return pivotpos; } template<class T> void QuickSort2(T arr[],int left,int right) { if(left<right) //区间长度大于1则划分 { int pos=Partition(arr,left,right); QuickSort(arr,left,pos-1); QuickSort(arr,pos+1,right); } } //实验表明在排序区间大小在5-25之间时,之间插入排序效率比普通快速排序高,而且直接插入排序在序列基本有序时效率非常高,所以我们借此改进快速排序 //方法:1,选取序列前中后三元素的中值最为基准元素,并把它放在后端,这样有利于防止快速排序退化。2,快速排序在序列元素很少时效率不及一般排序高,故我们采取在快速排序划分区间,使区间足够小时(这时序列也基本有序了)采取直接插入排序完成最后排序。
这两种方法可以使快速排序效率提高20%-25% const int M_M=15; //区间足够小的上限 template<class T> T& median3(T arr[],int left,int right) { int mid=(left+right)/2,k=left; //使k指向最小元素 if(arr[mid]<arr[k]) k=mid; if(arr[right]<arr[k]) k=right; //三者中最小元素放在arr[left]中 if(left!=k) swap(arr[left],arr[k]); if(mid!=right && arr[mid]<arr[right]) swap(arr[mid],arr[right]); //中间元素放在arr[right]中 return arr[right]; } template<class T> int Partition3(T arr[],int low,int high) { int i=low,j=high-1; T pivot=median3(arr,low,high); //这里我们是把基准选在末端(此时末端经median调整,已成为前中后三元素的中间值) //这里没必要用一个判断if(low<high),因为QuickSort中已经保证high-low>=1(这里是指上面的快速排序)下面的保证了Length>=M_M+1,及区间长度大于等于2。
//当然当区间长度大于2,for循环执行回进行调整,若等于2,他会在后面的if(arr[i]>pivot)中进行比较调整 for(;i<j;) //i<j判断不能取等号,当出现i==j时说明i j指向的元素都等于pivot,此时可以定位pivot了 { while( arr[i]<pivot) i++; //不能把i<j 判断放在下面两个循环控制中,而在for中不出现,如这样做:当最后一个元素最大时,函数却返回high-1 这肯定错 while( arr[j]>pivot) j--; if(i<j) { swap(arr[i],arr[j]); i++;j--; } else break; } if(arr[i]>pivot) //流程回到这里说明arr[i]>=pivot,当然arr[i]==pivot时没必要交换 { arr[high]=arr[i]; arr[i]=pivot; } return i; } template<class T> void QuickSort3(T arr[],int left,int right) { if(right-left<=M_M) return; int pos=Partition1(arr,left,right); QuickSort1(arr,left,pos-1); QuickSort1(arr,pos+1,right); } template<class T> void HybridSort(T arr[],int left,int right) { QuickSort3(arr,left,right); //利用快速排序进行划分,是序列基本有序 DirectSort2(arr,left,right); } //基数排序(MSD和LSD) //MSD const int radix=10; //基数 const int N=3; //假定是三位数 const int M=5; //进行直接插入排序的序列长度上限 template<class T> int getDigit1(T& elem,int d) { string s; int allbit[N+1],i,j; for(int i=1;i<=N;i++) allbit[i]=0; ostringstream oss; oss<< elem; s=oss.str(); for(i=1,j=s.length()-1;j>=0;i++,j--) //按elem得到的字符串反向放到各位上 allbit[i]=s[j]-48; return allbit[d]; } template<class T> void MSDradixSort(T arr[],int left,int right,int d) { //MSD排序,从高位到底对序列进行划分排序,d是第几位数,d=1时时最低位 //left和right是待排序列的始端和终端 int i,j,p1,p2,count[radix]; if(d<=0) return; if(right-left+1<=M) { DirectSort2(arr,left,right); return;} //当序列长度小于等于M时进行直接插入排序 T* auxArry=new T[right-left+1]; //动态分配辅助数组 for(j=0;j<radix;j++) count[j]=0; for(i=left;i<=right;i++) //统计各桶元素个数 count[getDigit1(arr[i],d)]++; for(i=1;i<radix;i++) //安排各桶元素存放位置 count[i]=count[i]+count[i-1]; for(j=left;j<=right;j++) //得到按d位非递减有序的序列 { i=getDigit1(arr[j],d); auxArry[count[i]-1]=arr[j]; count[i]--; } for(i=left,j=0;i<=right;i++,j++) //返回到原来数组中 arr[i]=auxArry[j]; delete []auxArry; for(j=0;j<radix;j++) { p1=count[j]; p2=count[j+1]-1; MSDradixSort(arr,p1,p2,d-1); //递归排序 } } //LSD(用静态链表实现,若用数组实现可以放在上面的MSD) const int DefaultSize=10; /*const int N=3; //排序码的位数假定为三位 const int radix=10; //基数为10 */ //这里的N 和radix和上面的一样 template<class T> struct Element //元素类型 { T key; //关键字 int link; //链接指针 // field other; 其他数据域 Element():link(0){} Element(T k,int n=0):key(k),link(n){} }; template<class T> class StaticLinkedList //静态链表类型(会建立循环链表) { public: StaticLinkedList(int sz=DefaultSize):maxSize(sz),n(0){ vec=new Element<T>[maxSize]; vec[0].link=1; } StaticLinkedList(Element<T> arr[],int nn); ~StaticLinkedList(){ delete []vec;} Element<T>& operator [] (int i) { return vec[i];} const Element<T>& operator [] (int i) const { return vec[i]; } int Length() const { return n;} //静态链表长度 void Display(ostream& out); private: Element<T>* vec; //存储待排序元素的向量 int maxSize,n; //最大尺寸和当前大小 }; template<class T> void StaticLinkedList<T>::Display(ostream& out) { for(int i=vec[0].link;i!=0;i=vec[i].link) cout << vec[i].key << " "; cout << endl; } template<class T> StaticLinkedList<T>::StaticLinkedList(Element<T> arr[],int nn):maxSize(2*nn),n(nn) { vec=new Element<T>[maxSize]; for(int i=1;i<=n;i++) vec[i]=arr[i-1]; vec[0].link=1; //vec[0]作为附加头结点 } template<class T> int getDigit2(Element<T>& e,int d) //这里的getDigit2与上面的getDigit1有所不同,故用数字加以区别 { //将key类型转换为字符串 int allbit[N]={0},i,j; //假定位数是三位 ostringstream oss; string dgs; oss << e.key; dgs=oss.str(); //得到关键字各位的整数表示 for(i=dgs.length()-1,j=N-1;i>=0;i--,j--) allbit[j]=dgs[i]-48; return allbit[d-1]; } //LSD基数排序 template<class T> void LSDradixSort(StaticLinkedList<T>& L,int d) //d表示关键字的位数 { int i,j,k,last,current,n=L.Length(); int front[radix],rear[radix]; //分别存放各桶的首尾指针 for(int i=0;i<n;i++) L[i].link=i+1; L[n].link=0; //形成循环链表 current=1; for(i=d;i>=1;i--) { for(j=0;j<radix;j++) front[j]=0; while(current!=0) { //得到各桶中的链表 k=getDigit2(L[current],i); if(front[k]==0) front[k]=current; else L[rear[k]].link=current; rear[k]=current; current=L[current].link; } j=0; while(front[j]==0) j++; //得到第一个非空桶头指针 L[0].link=current=front[j]; last=rear[j]; for(k=j+1;k<radix;k++) //得到按关键字d为排序的静态循环链表 { if(front[k]!=0) { L[last].link=front[k]; last=rear[k]; } } L[last].link=0; } } //锦标赛排序,利用胜者树实现 template<class T> class WinnerTree { public: static const T maxValue; WinnerTree(int sz=20):maxSize(sz),n(0){ t=new int[maxSize];} ~WinnerTree(){ delete []t;} int GetFirst() { return t[1];} //得到胜者的下标 bool Initial(T arr[],int size); bool RePlay(int i); void Play(int k,int lc,int rc); void Update() { e[t[1]]=maxValue;} //更新,即输出最终胜者,并将其调整为最大值,使其再也不能胜其他选手 T Winner() const { return (t[1]<=n)?e[t[1]]:0;} //t[i]内存储的是胜者的下标 int Winner(int i) const { return (t[i]<n)?t[i]:0;} int Winner(int a,int b) { return (e[a]<=e[b])?a:b;} //由于调用它的函数没有用常成员形式,故其不能为常成员 private: int maxSize; //允许的最大选手数 int n; //当前大小(允许的最大外部节点数 ) int lowExt; //最远层外部节点数 int offset; //按深度满节点数 int* t; //胜者树数组 T* e; //选手数组 }; template<class T> const T WinnerTree<T>::maxValue=INT_MAX; template<class T> bool WinnerTree<T>::Initial(T arr[],int size) { if(size>maxSize || size<2) return false; n=size; e=arr; int i,s; for(s=1;2*s<=n-1;s+=s); //计算2^log(n-1) lowExt=2*(n-s); offset=2*s-1; //处理最外层外部节点(最外层外部节点的个数肯定是偶数) for(i=2;i<=lowExt;i+=2) Play((i+offset)/2,i-1,i); //处理其他外部节点 if(n%2==0) //如果其他外部节点个数是偶数,则外部节点不需要与胜者节点比较 i=lowExt+2; else //是奇数,次外层外部节点的第一个节点与最远层内部节点的最后节点比较,这样比较后,剩下的外部节点数就为偶数了 { Play(n/2,t[n-1],lowExt+1); i=lowExt+3; } for(;i<=n;i+=2) //i为最左剩余节点,处理其余外部节点 Play((i-lowExt+n-1)/2,i-1,i); return true; } template<class T> void WinnerTree<T>::Play(int k,int lc,int rc) { t[k]=Winner(lc,rc); //在e[lc]和e[rc]中选出胜者 while(k>1 && k%2!=0) //内部节点的右子女编号都为偶数(根节点从1编号的完全二叉树),从右子女处向上比赛,直到根节点 { t[k/2]=Winner(t[k-1],t[k]); k/=2; } } template<class T> bool WinnerTree<T>::RePlay(int i) { //针对元素i值的改变,重新调整胜者树 if(i<=0 || i>n) return false; int k,lc,rc; if(i<=lowExt) //在最远层外部节点的情况 { k=(i+offset)/2; //得到父节点 lc=2*k-offset; //的到相应的左右子女 rc=lc+1; } else //在次外层外部节点上的情况 { k=(i-lowExt+n-1)/2; //得到父节点 if(2*k==n-1){ lc=t[n-1]; rc=i;} //如果其左子女为最远层最左端的内部节点 else { lc=2*k-n+1+lowExt; rc=lc+1;} } t[k]=Winner(lc,rc); k/=2; for(;k>=1;k/=2) //继续向父节点比赛直到根 if(2*k+1>n-1) t[k]=Winner(t[2*k],lowExt+1); //如果此时恰为内部节点与外部节点的比较情况 else t[k]=Winner(t[2*k],t[2*k+1]); return true; } template<class T> void TournamentSort(T a[],int left,int right) //锦标赛排序算法 { //建立胜者树WT,并将a[]复制到胜者树中,对他们进行排序,并把它重新返回到数组a[]中 //left和right分别表示待排序数组的起点和终点 int size=right-left+1; WinnerTree<T> WT(size); //胜者树对象 T *data=new T[size+1]; //存储输入数据,这相当于一个临时数组,因为在Initial中其对e未进行深复制,故不能直接将a[]传给Initial int i; for( i=1;i<=size;i++) data[i]=a[i+left-1]; //选手数组从1开始 WT.Initial(data,size); //初始化 for(i=0;i<size;i++) { a[i+left]=WT.Winner(); //输出胜者 WT.Update(); //修改胜者的值 WT.RePlay(WT.GetFirst()); if(WT.Winner()==WinnerTree<T>::maxValue) break; } delete []data; } //归并排序 template<class T> void merge(T arr1[],T arr2[],int left,int mid,int right) { //left,right 分别为arr1[]的始端和终端,mid为复制到arr2[]中后划分的中间点 for(int i=left;i<=right;i++) arr2[i]=arr1[i]; //将数组arr1[]复制到arr2[]中 int s1=left,s2=mid+1,t=left; while(s1<=mid && s2<=right) { if(arr2[s1]<=arr2[s2]) arr1[t++]=arr2[s1++]; else arr1[t++]=arr2[s2++]; } while(s1<=mid) arr1[t++]=arr2[s1++]; //若第一个表未检测完,复制第一个表 while(s2<=right) arr1[t++]=arr2[s2++]; //若第二表未检测完,复制第二个表 } template<class T> void mergeSort(T arr1[],T arr2[],int left,int right) { //要求arr2[]与arr1[]数组同类型等大 if(left>=right) return; int mid=(left+right)/2; //划分 mergeSort(arr1,arr2,left,mid); mergeSort(arr1,arr2,mid+1,right); //归并 merge(arr1,arr2,left,mid,right); } int _tmain(int argc, _TCHAR* argv[]) { int* parr=new int[1000]; srand(time(NULL)); for(int i=0;i<1000;i++) parr[i]=rand()%1000; HybridSort(parr,0,999); for(int i=0;i<1000;i++) { cout << parr[i] << " "; if((i+1)%20==0) //每隔20个输出换行号 cout << endl; } cout<< endl; delete []parr; int arr[]={1,3,2,4,6,5,7}; DirectSort2(arr,0,6); for(int i=0;i<=6;i++) cout << arr[i] << " "; cout << endl; return 0; }
c++中istringstream stream(line); 什么意思
流都很类似 比如:输入输出流 就是cin cout 从控制台读入写出 字符串流也类似,只是重定向到字符串 istringstream 是从字符串读 ostringstream是写到字符串中去,用法跟cin cout完全一样#include<sstream.h>是什么作用
我想你要是学C语言吧,,要学好先看看书, include有包含,包括,引用之意。#include<>说明下面的程序要引用<> 中的文件。
我也是刚学,,等下午看看给你个细致答案】 貌似C语言中的简称都是英文单词的前几个字
#include<sstream.h>是什么作用
C++的sstream标准库介绍 C++引入了ostringstream、istringstream、stringstream这三个类,要使用他们创建对象就必须包含sstream.h头文件。istringstream类用于执行C++风格的串流的输入操作。
ostringstream类用于执行C风格的串流的输出操作。
stringstream类同时可以支持C风格的串流的输入输出操作。
istringstream类是从istream(输入流类)和stringstreambase(c++字符串流基类)派生而来, ostringstream是从ostream(输出流类)和stringstreambase(c++字符串流基类)派生而来, stringstream则是从iostream(输入输出流类)和和stringstreambase(c++字符串流基类)派生而来。
C++的sstream标准库介绍C++的sstream标准库介绍
- ostringstream#include<sstream.h>是什么作用相关文档
- ostringstreamC++中ostringstream和ostream有什么区别,菜鸟求问
- ostringstreams1.str() ostr c++中什么意思
- ostringstreamstringbuf类是干什么用的解决方法
- ostringstreamc++怎样把double转为string
酷番云-618云上秒杀,香港1核2M 29/月,高防服务器20M 147/月 50M 450/月,续费同价!
官方网站:点击访问酷番云官网活动方案:优惠方案一(限时秒杀专场)有需要海外的可以看看,比较划算29月,建议年付划算,月付续费不同价,这个专区。国内节点可以看看,性能高IO为主, 比较少见。平常一般就100IO 左右。优惠方案二(高防专场)高防专区主要以高防为主,节点有宿迁,绍兴,成都,宁波等,节点挺多,都支持防火墙自助控制。续费同价以下专场。 优惠方案三(精选物理机)西南地区节点比较划算,赠送5...

搬瓦工VPS:新增荷兰机房“联通”线路的VPS,10Gbps带宽,可在美国cn2gia、日本软银、荷兰“联通”之间随意切换
搬瓦工今天正式对外开卖荷兰阿姆斯特丹机房走联通AS9929高端线路的VPS,官方标注为“NL - China Unicom Amsterdam(ENUL_9)”,三网都走联通高端网络,即使是在欧洲,国内访问也就是飞快。搬瓦工的依旧是10Gbps带宽,可以在美国cn2 gia、日本软银与荷兰AS9929之间免费切换。官方网站:https://bwh81.net优惠码:BWH3HYATVBJW,节约6...
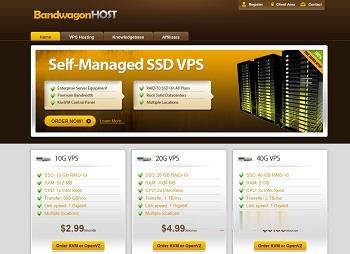
半月湾hmbcloud升级500Mbps带宽,原生VPS,$4.99/月
关于半月湾HMBCloud商家之前也有几篇那文章介绍过这个商家的产品,对于他们家的其他产品我都没有多加留意,而是对他们家的DC5机房很多人还是比较喜欢的,这个比我们有些比较熟悉的某商家DC6 DC9机房限时,而且半月湾HMBCloud商家是相对便宜的。关于半月湾DC5机房的方案选择和介绍:1、半月湾三网洛杉矶DC5 CN2 GIA同款DC6 DC9 1G内存 1TB流量 月$4.992、亲测选择半...
ostringstream为你推荐
-
xda论坛XDA论坛是中文网站吗?wazeMWC是什么?csonline2csol2房间人数是多少?能超过32人吗?求大神解答,尽可能详细,我需要CSOL2的情报谢谢。我mac地址克隆怎么克隆MAC地址?chrome系统Chrome OS是什么系统?y码亚洲码男女尺码是多少?qq博客怎么开QQ博客啊!华为总裁女儿为啥姓孟总裁文女主姓孟,女主父母抱错孩子,后来将错就错,养父母对女主很好腾讯年终奖腾讯外聘员工与正式员工的区别是什么?12种颜色十二种颜色的英文怎么读?