文章编号:10000887(2019)01007514
崔建斌 时间:2021-03-28 阅读:()
应用数学和力学编委会,ISSN10000887矩形到任意多边形区域的SchwarzChristoffel变换数值解法王玉风,姬安召,崔建斌(陇东学院能源工程学院,甘肃庆阳745000)摘要:运用SchwarzChristoffel变换方法,建立多边形区域到带状区域共形映射数学模型.
对于模型中的约束条件和奇异积分问题,根据Riemann(黎曼)原理,建立复参数与实参数互逆变换,消除非线性系统的约束条件;经过合理积分路径的确定,模型中的奇异积分转化为GaussJacobi(高斯雅可比)型积分;采用LevenbergMarquardt算法对非线性系统模型进行求解.
根据第一类椭圆函数性质,建立了矩形区域到带状区域共形映射数学模型,通过复参数椭圆函数的计算,得到矩形边界与带状区域边界的关系.
最后,对8点对称多边形区域与27点不规则条带状区域计算,将不规则封闭区域边界映射到矩形区域边界,矩形区域内的正交网格,通过变换之后在多边形区域内依然满足正交性,为研究不规则区域到规则区域映射的数值计算奠定基础.
关键词:SchwarzChristoffel变换;复参数椭圆函数;LevenbergMarquardt算法;矩形区域;多边形区域中图分类号:O242.
1文献标志码:ADOI:10.
21656/10000887.
390050引言在解决实际工程问题的过程中,SchwarzChristoffel变换(以下简称SC变换)模型有着重要的作用,SC变换能够把一个二维空间上复杂边界几何体映射到另一个二维空间上形状简单的几何体,从而可以简化工程中复杂边界问题的处理.
SC变换在油气地下渗流力学、岩土力学、流体力学和电磁学等研究领域有着广泛的应用.
目前有关SC变换数值计算方法有一些新的研究成果,王刚等[12]对多边形区域到上半平面映射和槽型区域映射方法进行研究,采用NewtonRaphson(牛顿拉夫森)迭代法进行求解.
祝江鸿等[34]采用SC变换Laurent级数模型导出地下开挖隧洞断面到单位圆映射的计算方法,但对于复杂开挖洞面,级数构成项较多,求解复杂.
皇甫鹏鹏等[5]、朱大勇等[6]和王润富[7]都以SC变换级数模型建立了多边形区域到单位圆映射模型,但级数模型构成复杂,计算量大,精度难以控制.
徐趁肖等[8]研究了复杂边界单连通区域共形映射模型,采用复变三角插值理论,利用法线迭代收敛方法,将任意复杂边界单连通区域问题映射到单位圆区域进行求解,但三角差值中涉及到复杂的级数计算.
王志良等[9]和王振武等[10]在研究浅埋隧道围岩应力场计算与地下矩形洞室应力分布复变函数解的过程中,57应用数学和力学,第40卷第1期2019年1月1日出版AppliedMathematicsandMechanicsVol.
40,No.
1,Jan.
1,2019收稿日期:20180129;修订日期:20180423基金项目:甘肃省自然科学基金(1606RJZM092;17JR5RM355);甘肃省高等学校科研项目(2017B61)作者简介:王玉风(1986—),女,讲师,硕士(通讯作者.
Email:yinyu413@163.
com).
采用共形映射公式为Laurent级数表示形式,其系数的求解方法复杂.
李明等[11]和袁林等[12]在矩形巷道围岩应力与变形黏弹性研究的过程中,建立了矩形巷道到单位圆的共形映射变换,但只考虑了矩形4个顶点与单位圆周的映射关系.
施高萍等[13]和陈凯等[14]在进行矩形巷道孔边应力的弹性分析时,建立了单位圆外域共形映射到洞室外域的映射函数,并以Laurent级数有限项对该问题进行了求解.
何峰等[15]和赵凯等[16]在矩形巷道围岩应力分布特征研究时,将圆形区域共形映射到矩形区域上,但只考虑了矩形3个顶点与圆形边界的对应关系.
文献[17]研究了多边形区域到条带状区域变换的理论模型,并建立带状区域到矩形映射数学模型.
通过上述研究成果可知,多边形区域到圆形、矩形区域的映射在求解不规则边界问题中有着重要的作用,尽管采用级数法可以将复杂区域边界映射到简单规则区域,但计算复杂,级数项及其系数确定较困难.
本文借鉴前人研究成果,对多边形区域到矩形区域映射的数学模型[17]进行数值计算方法研究.
采用一次参数变换,变换映射模型积分形式,建立其与GaussJacobi型积分的关系,提出了在积分路径中搜寻奇异点,进而寻求合理的积分子路径,在子路径采用修正GaussJacobi积分进行求解.
通过上述方法解决了计算过程中出现的奇异积分问题,同时也提高了积分精度,结合LevenbergMarquardt最优化算法求解非线性积分方程组,完成了从多边形区域到带状区域的映射的计算,然后结合第一类Jacobi椭圆函数,建立了带状区域与矩形区域的映射关系,通过求解复参数第一类Jacobi椭圆函数,完成带状区域到矩形区域映射的数值计算.
1基本模型在复平面w上有N(N≥4)边形,它的顶点与内角分别为wk和παk(k=1,2,…,N).
将带状区域边界上的点映射到w平面多边形区域顶点的SC变换[17]公式为w=A∫z0∏Nj=0fj(ξ)dξ+C,(1)其中,A为伸缩系数,C为变换中心,παk为w平面多边形内角,z为带状区域边界点,fj(ξ)为分段函数,具体表达式如下:fj(ξ)=e(z/2)(θ+-θ-),j=0,-i*sinhπ2(z-zj)éêêùúú{}αj-1,1≤j≤M,-i*sinh-π2(z-zj)éêêùúú{}αj-1,M+1≤j≤N,ìí(2)其中,i为虚数单位,M为带状区域下边界点的个数,N为多边形区域顶点的总个数,θ+为带状区域左边的无限远点的角度,θ-为带状区域右边的无限远点的角度,则θ+=θ-=π.
上半平面变换为矩形区域可由第一类椭圆积分函数表示,若已知矩形基本参数,则矩形映射到上半平面可由其反函数表示,即第一类椭圆函数.
借助第一类椭圆函数,将图1中的带状区域映射到矩形区域,映射变换[1718]可由式(3)表示:z=1πln(sn(u|l)),(3)其中,u为矩形区域,l为椭圆函数的模,由选择变换的矩形顶点决定.
映射点的对应关系如图1所示.
但在实际工程问题研究中,一般多边形区域是已知的,需求解与多边形顶点对应的矩形顶67王玉风姬安召崔建斌点及边界上的映射点.
根据Riemann原理,要确定式(1),则参数zk(k=1,2,…,N)中有3个点必须选定.
这样不妨假定z1=0,即选定映射为矩形长边的第一个顶点.
第二点取映射为矩形长边的第二个顶点,如图1中的z2点,该点的取值为映射模量,由选定矩形的长边与短边比值决定.
第三点取映射为矩形顶点的第四点,该点落在虚轴上,取值等于i,如图1中的z5=i.
但也可根据实际工程问题的需要,选择其他点.
在上述假定的条件下,式(1)中zk(k=1,2,…,N)满足下述条件:z=Re(zk)Re(zk+1)∪Im(zk)=i,{(4)即z必须位于带状区域边界上,点位次序为逆时针顺序.
图1矩形区域到带状区域变换示意图Fig.
1Therectangulardomaintothestripdomaintransformationdiagram若选定矩形长边第一个顶点位于坐标原点时,则式(1)中的C等于0,这样有利于问题的简化,因此可得多边形顶点wk(k=1,2,…,N)为wk=A∫zk0∏Nj=0fj(ξ)dξ.
(5)根据式(3),采用相邻两点之间的边长比值可消去伸缩系数,这样可以减少未知量的求解,因此可得wk+1-wkw2-w1=∫zk+1zk∏Nj=0fj(ξ)dξ∫z2z1∏Nj=0fj(ξ)dξ,k=2,3,…,N-2.
(6)令Ik=∫zk+1zk∏Nj=0fj(ξ)dξ,k=1,2,…,N-2,则式(6)可表示为Ik=I1wk+1-wkw2-w1,k=2,3,…,N-1.
(7)根据式(7),可得N-3个关系式,其中未知量为zk(k=1,2,…,N-3).
通过求解式(7)非线性积分方程组,可求得未知参数zk.
根据式(5)可求得伸缩系数A:A=w2-w1∫z2z1∏Nj=0fj(ξ)dξ.
(8)77矩形到任意多边形区域的SchwarzChristoffel变换数值解法2SchwarzChristoffel积分2.
1GaussJacobi型积分根据以上分析,为了求解带状区域到多边形区域映射参数问题式(7),必须计算式(6)的积分.
根据实际问题分析可知,式(6)积分路径在带状区域边界上,在带状区域的上下边界上含有无穷远点,无穷远点的处理方法可参考文献[18].
积分起点zk和终点zk+1为奇点,为了求解式(6)的奇异积分,对Ik做一次参数变换:令ξ=2zk+1-zk(z-zk+1)+1,代入式(7)可得Ik=zk+1-zk2·-iπzk+1-zk()4éêêùúúαk-1·∫1-1(1-ξ)0(1+ξ)αk-1fk(ξ)dξ,(9)其中fk(ξ)=e(1/2)(θ+-θ-)[(ξ-1)(zk+1-zk)/2+zk+1]*∏k-1j=1-i*sinhπ2ξ(zk+1-zk)+zk+zk+12-zjè÷éêêùúú{}αj-1*∏Mj=k+1-i*sinhπ2ξ(zk+1-zk)+zk+zk+12-zjè÷éêêùúú{}αj-1*∏Nj=M+1-i*sinh-π2ξ(zk+1-zk)+zk+zk+12-zjè÷éêêùúú{}αj-1.
为了将式(9)处理为GaussJacobi型积分,对fk(ξ)表达式中的第k个因子采用Taylor(泰勒)级数展开,取其线性部分.
保证求解变量z满足式(4)情况下,式(9)积分起点和终点都存在奇异点,起点奇异点为(1+ξ)αk-1项,终点奇异点为fk(ξ)表达式中的第k个因子.
因此,对于上式直接采用GaussJacobi型积分显然不合理,若对带状区域上边界或下边界对应点进行积分时,可将积分区间以区间的中点为界划分为两个子区间,进行两段积分,每段积分保证只含有一个奇异点,即(1+ξ)αk-1项.
通过上述修改,每个子区间能够满足GaussJacobi型积分式(9)条件.
根据文献[19],式(9)可表示为Ik≈∑nq=1Qqfk(xq),(10)其中,xq为权函数(1-t)0(1+t)αi-1在区间[-1,1]正交多项式的零点,Qq为权值,n为正交多项式的次数,根据文献[20],其值由积分Ik的精度决定,有关xq和Qq的求解参见文献[21].
2.
2合理积分路径的确定在采用迭代法求解式(7)时,积分Ik计算才是关键,文献[20]中研究结果表明可以通过增加正交多项式的次数提高积分精度.
本文通过试验研究表明积分路径长度对积分的精度也有一定程度的影响,因此为了保证积分精度,必须确定合理的积分路径长度.
在迭代过程中,当αk-1崔建斌Ik=∫zmidzk∏Nj=0fk(ξ)dξ+∫zk+1zmid∏Nj=0fk(ξ)dξ,式中,zmid为路径(zk,zk+1)的中点.
第2步确定积分路径长度,合理积分路径长度由下式确定:L=min1,minαzj-zkzmid-zkè÷{},j=1,2,…,N,式中,L为合理积分路径长度,m;α为积分路径长度加权因子,一般取α∈{0.
5,1,2},α取值较大时,则积分路径长度较长,但积分精度有所下降,反之,积分路径长度较短,精度有所增加,但计算时间也相应增加,本文取α=1.
第3步若L崔建斌变换的思路与第5步相似,在指数运算过程中,需要对这些变换点的实部做指数运算.
具体计算公式如下:r0,j=ln-eπxd+1+1-eπxd+2+eπxd+1è÷,j=d-2,ln-eπxj+3+eπxj+2-eπxj+4+eπxj+3è÷,j=k-3,ln-eπxN+eπxN-11+eπxNè÷,j=N-3,ìí其中,k=d-2,d-1,…,N-3;x表示变换点的实部.
通过上述6步的变换,建立N个复参数与N-3个实参数的关系.
3.
3实数到复参数变换进行实参数变换主要是因为采用Newton法、拟Newton法、共轭梯度法和LevenbergMarquardt等算法求解非线性方程组式(7)时,其Ik运算结果均为实数,而未知数为复参数.
若直接采用Ik的计算结果与其导数直接校正下一步的结果,无法保证满足式(4)的约束条件,因此必须建立实参数与复参数之间的对应关系,并且还能够将实参数的结果通过逆变换还原到复参数[17],同时未知数zk也满足式(4)的条件,其具体步骤如下.
第1步令Z′0=[0,0,…,0]N,此时已经包含z1=0,下面步骤对Z′0中的元素进行更新.
第2步第2个点到第b-1个点变换:z′0,k=∑kj=1er0,j,k=2,3,…,b-1,其中,z′0,k为第k个经过逆变换的复参数.
第3步第c+1个点到第d-1个点变换:z′0,k=i+∑k-2j=d-3er0,j,其中,k=c+1,c+2,…,d-1.
这里特别需要注意,j是从d-3倒序至k-2.
第4步b,c和d点的变换.
对于b点的变换,由无约束条件变换的第4步和初始化可得r0,b-1=12ln[(zb-zb-1)(xc-xc+1)],(13)其中,xc与xc+1分别为c点与c+1点的实部.
因为r0,b-1在无约束条件变换的第4步已经算出,根据初始化规则,结合图2,可得zb=xc,因此从式(13)可解出zb,即可得b点逆变换的计算公式:z′0,b=zb-1+xc+12+zb-1-xc+12è÷2+e2r0,b-1,其中,zb-1=Re(z′0,b-1),xc+1=Re(z′0,c+1),在第3与第4步已求出.
c点变换,z′0,c=z′0,b+i,d点变换,z′0,d=i.
第5步第b+1个点到第c-1个点变换.
在无约束变换过程中对初值做了对数变换,为了将其还原,首先令18矩形到任意多边形区域的SchwarzChristoffel变换数值解法hk=1-∑c-2k=be-∑kj=br0,j,k=b,1+∑kk=be-∑kj=br0,j-∑c-2k=k+1e-∑kj=br0,j,k=b+1,b+2,…,c-2,1+∑c-2k=be-∑kj=br0,j,k=c-1,ìí则z′0,k可表示为z′0,k=z′0,b-Relnhkhc-1è÷πéêêùúú.
第d+1个点到第N个点变换与上述方法类似,只需将求和部分的起点b改为d-2,终点c-2改为N-3即可.
可以证明,通过上述变换,z′0,k=zk.
3.
4LevenbergMarquardt算法参数优化由于非线性方程组的求解算法很多,鉴于篇幅有限,本文只采用了LevenbergMarquardt算法[25]求解式(7)非线性方程组.
LevenbergMarquardt算法中涉及到两个参数ρ与σ,根据图3,ρ与σ取值与迭代次数N、绝对误差e的关系曲线可以看出,ρ与σ取值对收敛速度有影响,通过反复的数值试验得出:ρ对收敛速度的影响很小,取ρ∈[0.
1,0.
9],而σ对收敛的速度的影响较大,取σ∈[0.
1,0.
5].
在参数ρ与σ满足上述取值时,对如图4所示规则的多边形区域进行计算,迭代45次就可以达到10-9次方的计算精度.
这里推荐ρ=0.
5,σ=0.
2.
图3LevenbergMarquardt算法中参数、迭代次数与绝对误差关系曲线Fig.
3Therelationshipcurvesofthenumberofiterations,theabsoluteerrorandtheparameterintheLevenbergMarquardtalgorithm3.
5第一类椭圆积分计算通过上述求解,基本完成了带状区域到多边形区域映射的计算,得到了带状区域边界与多边形区域边界的对应关系.
然而,要得到矩形边界的对应点,必须根据椭圆函数的模[17]进行第一类椭圆积分计算.
因为带状区域的宽度为1,而z1,zb,zc和zd决定了矩形左半部分,则右半部分可以通过解析延拓得到[18],因此椭圆函数的模取e-2πRe(zb-z1),得到矩形长宽参数,也就确定了矩形的4个顶点,椭圆积分计算方法可参见文献[26].
本文计算矩形长宽参数也是为了控制复参数椭圆函数计算,因为椭圆函数为一个双周期纯亚函数,其周期与矩形的长宽有关[18],若矩形的4个顶点确定之后,则椭圆函数周期也就确定了.
后续进行复参数第一类椭圆函数计算时,必须保证除矩形4个顶点之外,其他点受这4个顶点约束,按照逆时针顺序落在矩形边28王玉风姬安召崔建斌界上.
(a)矩形区域(b)对称多边形区域(a)Therectangulardomain(b)Thepolygonaldomain图4多边形区域到矩形映射变换Fig.
4Mappingtransformationofthepolygonaldomaintotherectangulardomain3.
6复参数第一类椭圆函数计算通过计算式(3),可得到带状区域到矩形区域的映射关系,但通过式(7)的求解,得到参数z为带状区域的复参数.
在文献[26]中,采用级数法、椭圆函数加法定理与精细积分相结合的方法对实参数的椭圆函数数值计算方法做了研究,现有部分计算类软件仅支持实参数椭圆函数的计算.
本文涉及到复参数椭圆函数的计算,借助Landen变换[27],可将第一类复参数椭圆函数数值算法描述如下.
第1步输入矩形区域边界u,输入由椭圆积分得到的矩形4个顶点.
若z中含有矩形上半平面的点,用矩形的宽度减去该点,将其变换到矩形的下半平面.
第2步若l10-3,令u=u1+l,k=(1-1-l)/(1+1-l)[]2,进行第1步递归调用,计算sn(u|l),dn(u|l),cn(u|l),否则进行第3步.
第4步令p=132*l4è÷6+42*l4è÷5+14*l4è÷4+5*l4è÷3+2*l4è÷2+1*l4è÷1,l=p2,u=u/1+l(),进行第1步递归调用,计算sn(u|l),dn(u|l),cn(u|l),否则进行第5步.
第5步计算椭圆函数sn(u|l)=(1+l)*sn′(u|l)1+l*[sn′(u|l)]2,38矩形到任意多边形区域的SchwarzChristoffel变换数值解法cn(u|l)=cn′(u|l)*cn′(u|l)1+l*[cn′(u|l)]2,dn(u|l)=1-l*[sn′(u|l)]21+l*[sn′(u|l)]2.
通过上述数值计算方法可以看出,在已知矩形区域边界时,可以将矩形区域映射到带状区域.
但文中的带状区域边界已经求出,因此,必须事先给出矩形边界初始化值u,通过函数sn(u|l)得到z值,根据所求z值与多边形区域到带状区域的z值相比较,若对应点位误差满足终止条件,则停止计算,否则采用Newton法矫正初始化值u,然后再次迭代计算z值,直到满足所需精度为止.
4精度评定通过上述分析,在求得变换参数u之后,将其代入式(3),求出带状区域边界z值,然后将z值代入式(6),可得w平面上|wk+1-wk|的计算值,最后利用已知的多边形区域顶点信息,可求解|wk+1-wk|的真值,根据真值与计算值,采用边长绝对误差进行精度评定:Δ=max(wk+1-wk)-A∫zk+1zk∏Nj=0fj(ξ)dξ(){},(14)其中k=1,2,…,N-1.
5算例分析平面封闭多边形区域如图4所示,为8个顶点的封闭多边形.
在变换时,选择多边形区域的第1,2,3,8共4个顶点,如图4(b)所示,这4个点分别对应矩形的4个顶点.
经过映射变换,将对称的多边形区域变换到矩形区域,顶点的对应关系如图4(a)实心方形点所示.
具体参数设置如下,在计算非线性方程组时,正交多项式次数为8,积分路径长度的加权因子α=1,非线性方程组的绝对误差为10-14,LevenbergMarquardt算法中的ρ=0.
5,σ=0.
2,在得到带状区域的映射点后,由矩形到带状区域的椭圆函数计算时设置的限差为10-14.
最后通过精度评定式(14)得到图4映射变换的精度为9.
60*10-13,具体的计算结果见表1.
表1多边形区域到矩形区域映射计算结果Table1Calculationresultsofthepolygonalregionstorectangularregionsmapping№.
polygonalregionvertexrectangularboundarypointnote1-1.
00+i*0.
001.
573159024665885selectthe1stvertexoftherectangle21.
00+i*0.
001.
573159024665885+i*3.
949032996567393selectthe2ndvertexoftherectangle33.
00+i*4.
00-1.
573159024665885+i*3.
949032996567393selectthe3rdvertexoftherectangle40.
75+i*4.
00-1.
573159024665885+i*3.
75308811495945450.
50+i*2.
00-1.
573159024665885+i*2.
9338960521378446-0.
50+i*2.
00-1.
573159024665885+i*1.
0151369444296447-0.
75+i*4.
00-1.
573159024665885+i*0.
19594488160795548-3.
00+i*4.
00-1.
573159024665885selectthe4thvertexoftherectangleA2.
182283881680463对于非对称区域,本文选取不规则条带状区域,将其边界离散,形成如图5所示的多边形区域.
在条带区域向矩形区域映射过程中,首先在带状区域中选取两点,这两点对应矩形的长48王玉风姬安召崔建斌边两个端点,然后按照逆时针方向选取其他两点,对应矩形的短边两个端点.
在图5不规则条带状区域中,选取第1点与第13点作为矩形的长边两个端点,其他两个点为第14点与第27点,作为矩形的短边两个端点.
在映射过程中,尽可能保证带状区域的长边方向与矩形区域的长边一致,这样能够避免在计算积分式(7)中产生群聚现象,因为映射变换过程要严格保证点位的次序,如果矩形短边上对应的点过多,可能导致某些映射点分布过于集中,从而导致式(7)积分值太小或趋近于0而发生群聚现象.
图5带状区域映射变换Fig.
5Mappingtransformationofthestripdomain通过上述两个示例可以看出,带状区域到矩形区域的映射,映射函数在映射区域上满足CauchyRiemann条件,因此矩形区域的正交网格映射到多边形区域上,网格仍然满足正交性,如图4、图5所示.
6结论1)矩形区域到多边形区域共形映射变换模型求解难点在于奇异积分计算、初值处理与复参数椭圆函数的计算.
从常规GaussJacobi型积分出发,对带状区域到多边形区域映射的模型进行一次参数变换,变换积分方程形式,以积分路径中的奇异点为界,寻求合理积分子路径,在子路径采用修正GaussJacobi积分方法有效地克服奇异积分计算的困难.
2)对于初值条件的处理,通过建立复参数与实参数函数关系,对其进行互逆运算,消除了约束条件,从而将常规非线性方程组求解LevenbergMarquardt算法应用到复参数奇异积分方程组的求解中.
3)在矩形区域到带状区域的映射变换过程中涉及的Jacobi椭圆函数,采用Landen变换,完成了复参数Jacobi椭圆函数的计算.
4)LevenbergMarquardt算法在求解多边形区域到带状区域映射的非线性系统是可行的,当参数ρ与σ选择适当,LevenbergMarquardt算法收敛较快.
5)通过8个顶点对称多边形到矩形映射,27个顶点的条带状区域到矩形映射的计算表明,本文给出的从矩形区域到多边形区域共形映射的数值算法具有可操作性.
参考文献(References):[1]王刚,许汉珍,顾王明,等.
数值许瓦尔兹克力斯托夫变换与数值高斯雅可比型积分[J].
海军工程大学学报,1994,1(2):2534.
(WANGGang,XUHanzhen,GUWangming,etal.
Numeri58矩形到任意多边形区域的SchwarzChristoffel变换数值解法calSchwarzChristoffeltransformationandnumericalGaussJacobiquadrature[J].
JournalofNavalAcademyofEngineering,1994,1(2):2534.
(inChinese))[2]王刚,陆小刚,顾王明.
槽形内域中的数值许瓦尔兹克力斯托夫保角变换[J].
海军工程大学学报,1995,1(4):1623.
(WANGGang,LUXiaogang,GUWangming.
NumericalSchwarzChristoffelconformalmappinginchannelregion[J].
JournalofNavalAcademyofEngineering,1995,1(4):1623.
(inChinese))[3]祝江鸿.
隧洞围岩应力复变函数分析法中的解析函数求解[J].
应用数学和力学,2013,34(4):345354.
(ZHUJianghong.
Analyticfunctionsinstressanalysisofthesurroundingrockforcavernswiththecomplexvariabletheory[J].
AppliedMathematicsandMechanics,2013,34(4):345354.
(inChinese))[4]祝江鸿,杨建辉,施高萍,等.
单位圆外域到任意开挖断面隧洞外域共形映射的计算方法[J].
岩土力学,2014,35(1):175183.
(ZHUJianghong,YANGJianhui,SHIGaoping,etal.
Calculatingmethodforconformalmappingfromexteriorofunitcircletoexteriorofcavernwitharbitraryexcavationcrosssection[J].
RockandSoilMechanics,2014,35(1):175183.
(inChinese))[5]皇甫鹏鹏,伍法权,郭松峰.
基于边界点搜索的洞室外域映射函数求解法[J].
岩石力学,2011,32(5):14181424.
(HUNAGFUPengpeng,WUFaquan,GUOSongfeng.
Anewmethodforcalculatingmappingfunctionofexternalareaofcavernwitharbitraryshapebasedonsearchingpointsonboundary[J].
RockandSoilMechanics,2011,32(5):14181424.
(inChinese))[6]朱大勇,钱七虎,周早生.
复杂形状洞室映射函数的新解法[J].
岩石力学与工程学报,1999,18(3):279282.
(ZHUDayong,QIANQihu,ZHOUZaosheng.
Newmethodforcalculatingmappingfunctionofopeningwithcomplexshape[J].
ChineseJournalofRockMechanicsandEngineering,1999,18(3):279282.
(inChinese))[7]王润富.
一种保角映射法及其微机实现[J].
河海大学学报,1991,19(1):8690.
(WANGRunfu.
Amethodofconformalmappinganditscomputerimplementation[J].
JournalofHohaiUniversity,1991,19(1):8690.
(inChinese))[8]徐趁肖,朱衡君,齐红元.
复杂边界单连通域共形映射解析建模研究[J].
工程数学学报,2002,19(4):135138.
(XUChenxiao,ZHUHengjun,QIHongyuan.
Analyticallymodelingofcomplicatedboundarysimplyconnectedregionconformalmapping[J].
JournalofEngineeringMathematics,2002,19(4):135138.
(inChinese))[9]王志良,申林方,姚激.
浅埋隧道围岩应力场的计算复变函数求解法[J].
岩土力学,2010,31(1):8690.
(WANGZhiliang,SHENLinfang,YAOJi.
Calculationofstressfieldinsurroundingrocksofshallowtunnelusingcomputationalfunctionofcomplexvariablemethod[J].
RockandSoilMechanics,2010,31(1):8690.
(inChinese))[10]王振武,牛铮铮,冯秀苓.
地下矩形洞室应力分布的复变函数解[J].
北华航天工业学院学报,2010,20(4):8690.
(WANGZhenwu,NIUZhengzheng,FENGXiuling.
Asemianalyticalelasticstresssolutionforperimeterstressesofrocksaroundarectangular[J].
JournalofNorthChinaInstituteofAerospaceEngineering,2010,20(4):8690.
(inChinese))[11]李明,茅献彪.
基于复变函数的矩形巷道围岩应力与变形粘弹性分析[J].
力学季刊,2011,32(2):195202.
(LIMing,MAOXianbiao.
Basedonthecomplexvariablefunctionsofrectangularroadwaysurroundingrockstressanddeformationviscoelasticanalysis[J].
ChineseQuarterlyofMechanics,2011,32(2):195202.
(inChinese))[12]袁林,高召宁,孟祥瑞.
基于复变函数法的矩形巷道应力集中系数黏弹性分析[J].
煤矿安全,2013,44(2):196200.
(YUANLin,GAOZhaoning,MENGXiangrui.
Viscoelasticanalysisof68王玉风姬安召崔建斌stressconcentrationcoefficientinrectangularroadwaybasedoncomplexvariablefunction[J].
SafetyinCoalMines,2013,44(2):196200.
(inChinese))[13]施高萍,祝江鸿,李保海,等.
矩形巷道孔边应力的弹性分析[J].
岩土力学,2014,35(9):25872601.
(SHIGaoping,ZHUJianghong,LIBaohai,etal.
Elasticanalysisofholeedgestressofrectangularroadway[J].
RockandSoilMechanics,2014,35(9):25872601.
(inChinese))[14]陈凯,唐治,崔乃鑫,等.
矩形巷道围岩应力解析解[J].
安全与环境学报,2015,15(3):124128.
(CHENKai,TANGZhi,CUINaixin,atel.
Analyticalsolutionofrectangularroadwaysurroundingrockstress[J].
JournalofSafetyandEnvironment,2015,15(3):124128.
(inChinese))[15]何峰,唐治,朱小景,等.
矩形巷道围岩应力分布特征[J].
数学的实践与认识,2015,45(20):128134.
(HEFeng,TANGZhi,ZHUXiaojing,etal.
Stressdistributioncharacteristicsofrectangularroadwaysurroundingrocks[J].
MathematicsinPracticeandTheory,2015,45(20):128134.
(inChinese))[16]赵凯,刘长武,张国良.
用弹性力学的复变函数法求解矩形硐室周边应力[J].
采矿与安全工程学报,2007,24(3):361365.
(ZHAOKai,LIUChangwu,ZHANGGuoliang.
Solutionforperimeterstressesofrocksaroundarectangularchamberusingthecomplexfunctionofelasticmechanics[J].
JournalofMiningandSafetyEngineering,2007,24(3):361365.
(inChinese))[17]HOWELLLH,TREFETHENLN.
AmodifiedSchwarzChristoffeltransformationforelongatedregions[J].
SocietyforIndustrialandAppliedMathematics,1990,11(5):928949.
[18]拉夫连季耶夫МА,沙巴特БВ.
复变函数论方法[M].
6版.
施祥林,夏定中,吕乃刚,译.
北京:高等教育出版社,2006.
(ЛАВРЕНТЬЕВМА,ШАБАТБВ.
MethodsoftheTheoryofComplexFunction[M].
6thed.
SHIXiangling,XIADingzhong,LNaigang,transl.
Beijing:HigherEducationPress,2006.
(Chineseversion))[19]COSTAMAGNAE.
AnewapproachtostandardSchwarzChristoffelformulacalculations[J].
MicrowaveandOpticalTechnologyLetters,2002,32(3):196199.
[20]DRISCOLLTA.
Algorithm843:improvementstotheSchwarzChristoffeltoolboxforMATLAB[J].
ACMTransactionsonMathematicalSoftware,2005,31(2):239251.
[21]崔建斌,姬安召,鲁洪江,等.
SchwarzChristoffel变换数值解法[J].
山东大学学报(理学版),2016,51(4):104111.
(CUIJianbin,JIAnzhao,LUHongjiang,etal.
NumericalsolutionofSchwarzChristoffeltransform[J].
JournalofShandongUniversity(NaturalScience),2015,51(4):104111.
(inChinese))[22]崔建斌,姬安召,王玉风,等.
单位圆到任意多边形区域的SchwarzChristoffel变换数值解法[J].
浙江大学学报(理学版),2017,44(2):161167.
(CUIJianbin,JIAnzhao,WANGYufeng,etal.
NumericalsolutionmethodforSchwarzChristoffeltransformfromunitcircletoarbitrarypolygonarea[J].
JournalofZhejiangUniversity(ScienceEdition),2017,44(2):161167.
(inChinese))[23]NATARAJANS,BORDASS,MAHAPATRADR.
NumericalintegrationoverarbitrarypolygonaldomainsbasedonSchwarzChristoffelconformalmapping[J].
InternationalJournalforNumericalMethodsinEngineering,2009,80(1):103134.
[24]CROWDYD.
TheSchwarzChristoffelmappingtoboundedmultiplyconnectedpolygonaldomains[J].
ProceedingsMathematicalPhysical&EngineeringScience,2005,146(2061):26532678.
[25]刘浩.
大规模非线性方程组和无约束优化方法研究[D].
博士学位论文.
南京:南京航空航天大78矩形到任意多边形区域的SchwarzChristoffel变换数值解法学,2008.
(LIUHao.
Researchonmethodsforlargescalenonlinearequationsandunconstrainedoptimization[D].
PhDThesis.
Nanjing:NanjingUniversityofAeronauticsandAstronautics,2008.
(inChinese))[26]姚征.
椭圆函数的精细积分改进算法[J].
数值计算与计算机应用,2008,29(4):251260.
(YAOZheng.
Theimprovedpreciseintegrationmethodforellipticfunctions[J].
JournalonNumericalMethodsandComputerApplications,2008,29(4):251260.
(inChinese))[27]ABRAMOWITZM,STEGUNIA.
HandbookofMathematicalFunctionsWithFormulas,Graphs,andMathematicalTables[M].
WashingtonDC:DoverPublications,1996.
NumericalSolutionofSchwarzChristoffelTransformationFromRectanglestoArbitraryPolygonalDomainsWANGYufeng,JIAnzhao,CUIJianbin(SchoolofEnergyEngineering,LongdongUniversity,Qingyang,Gansu745000,P.
R.
China)Abstract:WiththeSchwarzChristoffeltransformationmethod,amathematicalmodelofconformalmappingfrompolygonaldomainstostripdomainswasestablished.
Forconstraintconditionsandsingularintegralproblemsinthemodel,thereciprocaltransformationbetweencomplexparametersandrealparameterswasconductedbasedontheRiemannprinciple,whicheliminatesconstraintconditionsofthenonlinearsystem.
Bymeansofreasonableintegrationpaths,thesingularintegralinthemodelwastransformedintotheGaussJacobiintegral,andthenonlinearsystemmodelwassolvedwiththeLevenbergMarquardtalgorithm.
Accordingtothefirstclassellipticfunctioncharacteristics,themathematicalmodelofconformalmappingfromrectangulardomainstostripdomainswasbuilt,andtherelationshipbetweentherectangularboundaryandthestripboundarywasobtainedthroughcalculationofthecomplexparameterellipticfunction.
Atlast,an8pointpolygonaldomainanda27pointirregularstripdomainwerecalculatedtomaptheirregularcloseddomainboundarytotherectangulardomainboundary.
Theorthogonalgridintherectangulardomainstillmeetsorthogonalityinthepolygonaldomainaftermapping.
Thisstudyprovidesafoundationfornumericalcalculationofmappingfromirregulardomainstoregularones.
Keywords:SchwarzChristoffeltransformation;complexparameterellipticfunction;LevenbergMarquardtalgorithm;rectangulardomain;polygonaldomain88王玉风姬安召崔建斌引用本文/Citethispaper:王玉风,姬安召,崔建斌.
矩形到任意多边形区域的SchwarzChristoffel变换数值解法[J].
应用数学和力学,2019,40(1):7588.
WANGYufeng,JIAnzhao,CUIJianbin.
NumericalsolutionofSchwarzChristoffeltransformationfromrectanglestoarbitrarypolygonaldomains[J].
AppliedMathematicsandMechanics,2019,40(1):7588.
对于模型中的约束条件和奇异积分问题,根据Riemann(黎曼)原理,建立复参数与实参数互逆变换,消除非线性系统的约束条件;经过合理积分路径的确定,模型中的奇异积分转化为GaussJacobi(高斯雅可比)型积分;采用LevenbergMarquardt算法对非线性系统模型进行求解.
根据第一类椭圆函数性质,建立了矩形区域到带状区域共形映射数学模型,通过复参数椭圆函数的计算,得到矩形边界与带状区域边界的关系.
最后,对8点对称多边形区域与27点不规则条带状区域计算,将不规则封闭区域边界映射到矩形区域边界,矩形区域内的正交网格,通过变换之后在多边形区域内依然满足正交性,为研究不规则区域到规则区域映射的数值计算奠定基础.
关键词:SchwarzChristoffel变换;复参数椭圆函数;LevenbergMarquardt算法;矩形区域;多边形区域中图分类号:O242.
1文献标志码:ADOI:10.
21656/10000887.
390050引言在解决实际工程问题的过程中,SchwarzChristoffel变换(以下简称SC变换)模型有着重要的作用,SC变换能够把一个二维空间上复杂边界几何体映射到另一个二维空间上形状简单的几何体,从而可以简化工程中复杂边界问题的处理.
SC变换在油气地下渗流力学、岩土力学、流体力学和电磁学等研究领域有着广泛的应用.
目前有关SC变换数值计算方法有一些新的研究成果,王刚等[12]对多边形区域到上半平面映射和槽型区域映射方法进行研究,采用NewtonRaphson(牛顿拉夫森)迭代法进行求解.
祝江鸿等[34]采用SC变换Laurent级数模型导出地下开挖隧洞断面到单位圆映射的计算方法,但对于复杂开挖洞面,级数构成项较多,求解复杂.
皇甫鹏鹏等[5]、朱大勇等[6]和王润富[7]都以SC变换级数模型建立了多边形区域到单位圆映射模型,但级数模型构成复杂,计算量大,精度难以控制.
徐趁肖等[8]研究了复杂边界单连通区域共形映射模型,采用复变三角插值理论,利用法线迭代收敛方法,将任意复杂边界单连通区域问题映射到单位圆区域进行求解,但三角差值中涉及到复杂的级数计算.
王志良等[9]和王振武等[10]在研究浅埋隧道围岩应力场计算与地下矩形洞室应力分布复变函数解的过程中,57应用数学和力学,第40卷第1期2019年1月1日出版AppliedMathematicsandMechanicsVol.
40,No.
1,Jan.
1,2019收稿日期:20180129;修订日期:20180423基金项目:甘肃省自然科学基金(1606RJZM092;17JR5RM355);甘肃省高等学校科研项目(2017B61)作者简介:王玉风(1986—),女,讲师,硕士(通讯作者.
Email:yinyu413@163.
com).
采用共形映射公式为Laurent级数表示形式,其系数的求解方法复杂.
李明等[11]和袁林等[12]在矩形巷道围岩应力与变形黏弹性研究的过程中,建立了矩形巷道到单位圆的共形映射变换,但只考虑了矩形4个顶点与单位圆周的映射关系.
施高萍等[13]和陈凯等[14]在进行矩形巷道孔边应力的弹性分析时,建立了单位圆外域共形映射到洞室外域的映射函数,并以Laurent级数有限项对该问题进行了求解.
何峰等[15]和赵凯等[16]在矩形巷道围岩应力分布特征研究时,将圆形区域共形映射到矩形区域上,但只考虑了矩形3个顶点与圆形边界的对应关系.
文献[17]研究了多边形区域到条带状区域变换的理论模型,并建立带状区域到矩形映射数学模型.
通过上述研究成果可知,多边形区域到圆形、矩形区域的映射在求解不规则边界问题中有着重要的作用,尽管采用级数法可以将复杂区域边界映射到简单规则区域,但计算复杂,级数项及其系数确定较困难.
本文借鉴前人研究成果,对多边形区域到矩形区域映射的数学模型[17]进行数值计算方法研究.
采用一次参数变换,变换映射模型积分形式,建立其与GaussJacobi型积分的关系,提出了在积分路径中搜寻奇异点,进而寻求合理的积分子路径,在子路径采用修正GaussJacobi积分进行求解.
通过上述方法解决了计算过程中出现的奇异积分问题,同时也提高了积分精度,结合LevenbergMarquardt最优化算法求解非线性积分方程组,完成了从多边形区域到带状区域的映射的计算,然后结合第一类Jacobi椭圆函数,建立了带状区域与矩形区域的映射关系,通过求解复参数第一类Jacobi椭圆函数,完成带状区域到矩形区域映射的数值计算.
1基本模型在复平面w上有N(N≥4)边形,它的顶点与内角分别为wk和παk(k=1,2,…,N).
将带状区域边界上的点映射到w平面多边形区域顶点的SC变换[17]公式为w=A∫z0∏Nj=0fj(ξ)dξ+C,(1)其中,A为伸缩系数,C为变换中心,παk为w平面多边形内角,z为带状区域边界点,fj(ξ)为分段函数,具体表达式如下:fj(ξ)=e(z/2)(θ+-θ-),j=0,-i*sinhπ2(z-zj)éêêùúú{}αj-1,1≤j≤M,-i*sinh-π2(z-zj)éêêùúú{}αj-1,M+1≤j≤N,ìí(2)其中,i为虚数单位,M为带状区域下边界点的个数,N为多边形区域顶点的总个数,θ+为带状区域左边的无限远点的角度,θ-为带状区域右边的无限远点的角度,则θ+=θ-=π.
上半平面变换为矩形区域可由第一类椭圆积分函数表示,若已知矩形基本参数,则矩形映射到上半平面可由其反函数表示,即第一类椭圆函数.
借助第一类椭圆函数,将图1中的带状区域映射到矩形区域,映射变换[1718]可由式(3)表示:z=1πln(sn(u|l)),(3)其中,u为矩形区域,l为椭圆函数的模,由选择变换的矩形顶点决定.
映射点的对应关系如图1所示.
但在实际工程问题研究中,一般多边形区域是已知的,需求解与多边形顶点对应的矩形顶67王玉风姬安召崔建斌点及边界上的映射点.
根据Riemann原理,要确定式(1),则参数zk(k=1,2,…,N)中有3个点必须选定.
这样不妨假定z1=0,即选定映射为矩形长边的第一个顶点.
第二点取映射为矩形长边的第二个顶点,如图1中的z2点,该点的取值为映射模量,由选定矩形的长边与短边比值决定.
第三点取映射为矩形顶点的第四点,该点落在虚轴上,取值等于i,如图1中的z5=i.
但也可根据实际工程问题的需要,选择其他点.
在上述假定的条件下,式(1)中zk(k=1,2,…,N)满足下述条件:z=Re(zk)Re(zk+1)∪Im(zk)=i,{(4)即z必须位于带状区域边界上,点位次序为逆时针顺序.
图1矩形区域到带状区域变换示意图Fig.
1Therectangulardomaintothestripdomaintransformationdiagram若选定矩形长边第一个顶点位于坐标原点时,则式(1)中的C等于0,这样有利于问题的简化,因此可得多边形顶点wk(k=1,2,…,N)为wk=A∫zk0∏Nj=0fj(ξ)dξ.
(5)根据式(3),采用相邻两点之间的边长比值可消去伸缩系数,这样可以减少未知量的求解,因此可得wk+1-wkw2-w1=∫zk+1zk∏Nj=0fj(ξ)dξ∫z2z1∏Nj=0fj(ξ)dξ,k=2,3,…,N-2.
(6)令Ik=∫zk+1zk∏Nj=0fj(ξ)dξ,k=1,2,…,N-2,则式(6)可表示为Ik=I1wk+1-wkw2-w1,k=2,3,…,N-1.
(7)根据式(7),可得N-3个关系式,其中未知量为zk(k=1,2,…,N-3).
通过求解式(7)非线性积分方程组,可求得未知参数zk.
根据式(5)可求得伸缩系数A:A=w2-w1∫z2z1∏Nj=0fj(ξ)dξ.
(8)77矩形到任意多边形区域的SchwarzChristoffel变换数值解法2SchwarzChristoffel积分2.
1GaussJacobi型积分根据以上分析,为了求解带状区域到多边形区域映射参数问题式(7),必须计算式(6)的积分.
根据实际问题分析可知,式(6)积分路径在带状区域边界上,在带状区域的上下边界上含有无穷远点,无穷远点的处理方法可参考文献[18].
积分起点zk和终点zk+1为奇点,为了求解式(6)的奇异积分,对Ik做一次参数变换:令ξ=2zk+1-zk(z-zk+1)+1,代入式(7)可得Ik=zk+1-zk2·-iπzk+1-zk()4éêêùúúαk-1·∫1-1(1-ξ)0(1+ξ)αk-1fk(ξ)dξ,(9)其中fk(ξ)=e(1/2)(θ+-θ-)[(ξ-1)(zk+1-zk)/2+zk+1]*∏k-1j=1-i*sinhπ2ξ(zk+1-zk)+zk+zk+12-zjè÷éêêùúú{}αj-1*∏Mj=k+1-i*sinhπ2ξ(zk+1-zk)+zk+zk+12-zjè÷éêêùúú{}αj-1*∏Nj=M+1-i*sinh-π2ξ(zk+1-zk)+zk+zk+12-zjè÷éêêùúú{}αj-1.
为了将式(9)处理为GaussJacobi型积分,对fk(ξ)表达式中的第k个因子采用Taylor(泰勒)级数展开,取其线性部分.
保证求解变量z满足式(4)情况下,式(9)积分起点和终点都存在奇异点,起点奇异点为(1+ξ)αk-1项,终点奇异点为fk(ξ)表达式中的第k个因子.
因此,对于上式直接采用GaussJacobi型积分显然不合理,若对带状区域上边界或下边界对应点进行积分时,可将积分区间以区间的中点为界划分为两个子区间,进行两段积分,每段积分保证只含有一个奇异点,即(1+ξ)αk-1项.
通过上述修改,每个子区间能够满足GaussJacobi型积分式(9)条件.
根据文献[19],式(9)可表示为Ik≈∑nq=1Qqfk(xq),(10)其中,xq为权函数(1-t)0(1+t)αi-1在区间[-1,1]正交多项式的零点,Qq为权值,n为正交多项式的次数,根据文献[20],其值由积分Ik的精度决定,有关xq和Qq的求解参见文献[21].
2.
2合理积分路径的确定在采用迭代法求解式(7)时,积分Ik计算才是关键,文献[20]中研究结果表明可以通过增加正交多项式的次数提高积分精度.
本文通过试验研究表明积分路径长度对积分的精度也有一定程度的影响,因此为了保证积分精度,必须确定合理的积分路径长度.
在迭代过程中,当αk-1崔建斌Ik=∫zmidzk∏Nj=0fk(ξ)dξ+∫zk+1zmid∏Nj=0fk(ξ)dξ,式中,zmid为路径(zk,zk+1)的中点.
第2步确定积分路径长度,合理积分路径长度由下式确定:L=min1,minαzj-zkzmid-zkè÷{},j=1,2,…,N,式中,L为合理积分路径长度,m;α为积分路径长度加权因子,一般取α∈{0.
5,1,2},α取值较大时,则积分路径长度较长,但积分精度有所下降,反之,积分路径长度较短,精度有所增加,但计算时间也相应增加,本文取α=1.
第3步若L崔建斌变换的思路与第5步相似,在指数运算过程中,需要对这些变换点的实部做指数运算.
具体计算公式如下:r0,j=ln-eπxd+1+1-eπxd+2+eπxd+1è÷,j=d-2,ln-eπxj+3+eπxj+2-eπxj+4+eπxj+3è÷,j=k-3,ln-eπxN+eπxN-11+eπxNè÷,j=N-3,ìí其中,k=d-2,d-1,…,N-3;x表示变换点的实部.
通过上述6步的变换,建立N个复参数与N-3个实参数的关系.
3.
3实数到复参数变换进行实参数变换主要是因为采用Newton法、拟Newton法、共轭梯度法和LevenbergMarquardt等算法求解非线性方程组式(7)时,其Ik运算结果均为实数,而未知数为复参数.
若直接采用Ik的计算结果与其导数直接校正下一步的结果,无法保证满足式(4)的约束条件,因此必须建立实参数与复参数之间的对应关系,并且还能够将实参数的结果通过逆变换还原到复参数[17],同时未知数zk也满足式(4)的条件,其具体步骤如下.
第1步令Z′0=[0,0,…,0]N,此时已经包含z1=0,下面步骤对Z′0中的元素进行更新.
第2步第2个点到第b-1个点变换:z′0,k=∑kj=1er0,j,k=2,3,…,b-1,其中,z′0,k为第k个经过逆变换的复参数.
第3步第c+1个点到第d-1个点变换:z′0,k=i+∑k-2j=d-3er0,j,其中,k=c+1,c+2,…,d-1.
这里特别需要注意,j是从d-3倒序至k-2.
第4步b,c和d点的变换.
对于b点的变换,由无约束条件变换的第4步和初始化可得r0,b-1=12ln[(zb-zb-1)(xc-xc+1)],(13)其中,xc与xc+1分别为c点与c+1点的实部.
因为r0,b-1在无约束条件变换的第4步已经算出,根据初始化规则,结合图2,可得zb=xc,因此从式(13)可解出zb,即可得b点逆变换的计算公式:z′0,b=zb-1+xc+12+zb-1-xc+12è÷2+e2r0,b-1,其中,zb-1=Re(z′0,b-1),xc+1=Re(z′0,c+1),在第3与第4步已求出.
c点变换,z′0,c=z′0,b+i,d点变换,z′0,d=i.
第5步第b+1个点到第c-1个点变换.
在无约束变换过程中对初值做了对数变换,为了将其还原,首先令18矩形到任意多边形区域的SchwarzChristoffel变换数值解法hk=1-∑c-2k=be-∑kj=br0,j,k=b,1+∑kk=be-∑kj=br0,j-∑c-2k=k+1e-∑kj=br0,j,k=b+1,b+2,…,c-2,1+∑c-2k=be-∑kj=br0,j,k=c-1,ìí则z′0,k可表示为z′0,k=z′0,b-Relnhkhc-1è÷πéêêùúú.
第d+1个点到第N个点变换与上述方法类似,只需将求和部分的起点b改为d-2,终点c-2改为N-3即可.
可以证明,通过上述变换,z′0,k=zk.
3.
4LevenbergMarquardt算法参数优化由于非线性方程组的求解算法很多,鉴于篇幅有限,本文只采用了LevenbergMarquardt算法[25]求解式(7)非线性方程组.
LevenbergMarquardt算法中涉及到两个参数ρ与σ,根据图3,ρ与σ取值与迭代次数N、绝对误差e的关系曲线可以看出,ρ与σ取值对收敛速度有影响,通过反复的数值试验得出:ρ对收敛速度的影响很小,取ρ∈[0.
1,0.
9],而σ对收敛的速度的影响较大,取σ∈[0.
1,0.
5].
在参数ρ与σ满足上述取值时,对如图4所示规则的多边形区域进行计算,迭代45次就可以达到10-9次方的计算精度.
这里推荐ρ=0.
5,σ=0.
2.
图3LevenbergMarquardt算法中参数、迭代次数与绝对误差关系曲线Fig.
3Therelationshipcurvesofthenumberofiterations,theabsoluteerrorandtheparameterintheLevenbergMarquardtalgorithm3.
5第一类椭圆积分计算通过上述求解,基本完成了带状区域到多边形区域映射的计算,得到了带状区域边界与多边形区域边界的对应关系.
然而,要得到矩形边界的对应点,必须根据椭圆函数的模[17]进行第一类椭圆积分计算.
因为带状区域的宽度为1,而z1,zb,zc和zd决定了矩形左半部分,则右半部分可以通过解析延拓得到[18],因此椭圆函数的模取e-2πRe(zb-z1),得到矩形长宽参数,也就确定了矩形的4个顶点,椭圆积分计算方法可参见文献[26].
本文计算矩形长宽参数也是为了控制复参数椭圆函数计算,因为椭圆函数为一个双周期纯亚函数,其周期与矩形的长宽有关[18],若矩形的4个顶点确定之后,则椭圆函数周期也就确定了.
后续进行复参数第一类椭圆函数计算时,必须保证除矩形4个顶点之外,其他点受这4个顶点约束,按照逆时针顺序落在矩形边28王玉风姬安召崔建斌界上.
(a)矩形区域(b)对称多边形区域(a)Therectangulardomain(b)Thepolygonaldomain图4多边形区域到矩形映射变换Fig.
4Mappingtransformationofthepolygonaldomaintotherectangulardomain3.
6复参数第一类椭圆函数计算通过计算式(3),可得到带状区域到矩形区域的映射关系,但通过式(7)的求解,得到参数z为带状区域的复参数.
在文献[26]中,采用级数法、椭圆函数加法定理与精细积分相结合的方法对实参数的椭圆函数数值计算方法做了研究,现有部分计算类软件仅支持实参数椭圆函数的计算.
本文涉及到复参数椭圆函数的计算,借助Landen变换[27],可将第一类复参数椭圆函数数值算法描述如下.
第1步输入矩形区域边界u,输入由椭圆积分得到的矩形4个顶点.
若z中含有矩形上半平面的点,用矩形的宽度减去该点,将其变换到矩形的下半平面.
第2步若l10-3,令u=u1+l,k=(1-1-l)/(1+1-l)[]2,进行第1步递归调用,计算sn(u|l),dn(u|l),cn(u|l),否则进行第3步.
第4步令p=132*l4è÷6+42*l4è÷5+14*l4è÷4+5*l4è÷3+2*l4è÷2+1*l4è÷1,l=p2,u=u/1+l(),进行第1步递归调用,计算sn(u|l),dn(u|l),cn(u|l),否则进行第5步.
第5步计算椭圆函数sn(u|l)=(1+l)*sn′(u|l)1+l*[sn′(u|l)]2,38矩形到任意多边形区域的SchwarzChristoffel变换数值解法cn(u|l)=cn′(u|l)*cn′(u|l)1+l*[cn′(u|l)]2,dn(u|l)=1-l*[sn′(u|l)]21+l*[sn′(u|l)]2.
通过上述数值计算方法可以看出,在已知矩形区域边界时,可以将矩形区域映射到带状区域.
但文中的带状区域边界已经求出,因此,必须事先给出矩形边界初始化值u,通过函数sn(u|l)得到z值,根据所求z值与多边形区域到带状区域的z值相比较,若对应点位误差满足终止条件,则停止计算,否则采用Newton法矫正初始化值u,然后再次迭代计算z值,直到满足所需精度为止.
4精度评定通过上述分析,在求得变换参数u之后,将其代入式(3),求出带状区域边界z值,然后将z值代入式(6),可得w平面上|wk+1-wk|的计算值,最后利用已知的多边形区域顶点信息,可求解|wk+1-wk|的真值,根据真值与计算值,采用边长绝对误差进行精度评定:Δ=max(wk+1-wk)-A∫zk+1zk∏Nj=0fj(ξ)dξ(){},(14)其中k=1,2,…,N-1.
5算例分析平面封闭多边形区域如图4所示,为8个顶点的封闭多边形.
在变换时,选择多边形区域的第1,2,3,8共4个顶点,如图4(b)所示,这4个点分别对应矩形的4个顶点.
经过映射变换,将对称的多边形区域变换到矩形区域,顶点的对应关系如图4(a)实心方形点所示.
具体参数设置如下,在计算非线性方程组时,正交多项式次数为8,积分路径长度的加权因子α=1,非线性方程组的绝对误差为10-14,LevenbergMarquardt算法中的ρ=0.
5,σ=0.
2,在得到带状区域的映射点后,由矩形到带状区域的椭圆函数计算时设置的限差为10-14.
最后通过精度评定式(14)得到图4映射变换的精度为9.
60*10-13,具体的计算结果见表1.
表1多边形区域到矩形区域映射计算结果Table1Calculationresultsofthepolygonalregionstorectangularregionsmapping№.
polygonalregionvertexrectangularboundarypointnote1-1.
00+i*0.
001.
573159024665885selectthe1stvertexoftherectangle21.
00+i*0.
001.
573159024665885+i*3.
949032996567393selectthe2ndvertexoftherectangle33.
00+i*4.
00-1.
573159024665885+i*3.
949032996567393selectthe3rdvertexoftherectangle40.
75+i*4.
00-1.
573159024665885+i*3.
75308811495945450.
50+i*2.
00-1.
573159024665885+i*2.
9338960521378446-0.
50+i*2.
00-1.
573159024665885+i*1.
0151369444296447-0.
75+i*4.
00-1.
573159024665885+i*0.
19594488160795548-3.
00+i*4.
00-1.
573159024665885selectthe4thvertexoftherectangleA2.
182283881680463对于非对称区域,本文选取不规则条带状区域,将其边界离散,形成如图5所示的多边形区域.
在条带区域向矩形区域映射过程中,首先在带状区域中选取两点,这两点对应矩形的长48王玉风姬安召崔建斌边两个端点,然后按照逆时针方向选取其他两点,对应矩形的短边两个端点.
在图5不规则条带状区域中,选取第1点与第13点作为矩形的长边两个端点,其他两个点为第14点与第27点,作为矩形的短边两个端点.
在映射过程中,尽可能保证带状区域的长边方向与矩形区域的长边一致,这样能够避免在计算积分式(7)中产生群聚现象,因为映射变换过程要严格保证点位的次序,如果矩形短边上对应的点过多,可能导致某些映射点分布过于集中,从而导致式(7)积分值太小或趋近于0而发生群聚现象.
图5带状区域映射变换Fig.
5Mappingtransformationofthestripdomain通过上述两个示例可以看出,带状区域到矩形区域的映射,映射函数在映射区域上满足CauchyRiemann条件,因此矩形区域的正交网格映射到多边形区域上,网格仍然满足正交性,如图4、图5所示.
6结论1)矩形区域到多边形区域共形映射变换模型求解难点在于奇异积分计算、初值处理与复参数椭圆函数的计算.
从常规GaussJacobi型积分出发,对带状区域到多边形区域映射的模型进行一次参数变换,变换积分方程形式,以积分路径中的奇异点为界,寻求合理积分子路径,在子路径采用修正GaussJacobi积分方法有效地克服奇异积分计算的困难.
2)对于初值条件的处理,通过建立复参数与实参数函数关系,对其进行互逆运算,消除了约束条件,从而将常规非线性方程组求解LevenbergMarquardt算法应用到复参数奇异积分方程组的求解中.
3)在矩形区域到带状区域的映射变换过程中涉及的Jacobi椭圆函数,采用Landen变换,完成了复参数Jacobi椭圆函数的计算.
4)LevenbergMarquardt算法在求解多边形区域到带状区域映射的非线性系统是可行的,当参数ρ与σ选择适当,LevenbergMarquardt算法收敛较快.
5)通过8个顶点对称多边形到矩形映射,27个顶点的条带状区域到矩形映射的计算表明,本文给出的从矩形区域到多边形区域共形映射的数值算法具有可操作性.
参考文献(References):[1]王刚,许汉珍,顾王明,等.
数值许瓦尔兹克力斯托夫变换与数值高斯雅可比型积分[J].
海军工程大学学报,1994,1(2):2534.
(WANGGang,XUHanzhen,GUWangming,etal.
Numeri58矩形到任意多边形区域的SchwarzChristoffel变换数值解法calSchwarzChristoffeltransformationandnumericalGaussJacobiquadrature[J].
JournalofNavalAcademyofEngineering,1994,1(2):2534.
(inChinese))[2]王刚,陆小刚,顾王明.
槽形内域中的数值许瓦尔兹克力斯托夫保角变换[J].
海军工程大学学报,1995,1(4):1623.
(WANGGang,LUXiaogang,GUWangming.
NumericalSchwarzChristoffelconformalmappinginchannelregion[J].
JournalofNavalAcademyofEngineering,1995,1(4):1623.
(inChinese))[3]祝江鸿.
隧洞围岩应力复变函数分析法中的解析函数求解[J].
应用数学和力学,2013,34(4):345354.
(ZHUJianghong.
Analyticfunctionsinstressanalysisofthesurroundingrockforcavernswiththecomplexvariabletheory[J].
AppliedMathematicsandMechanics,2013,34(4):345354.
(inChinese))[4]祝江鸿,杨建辉,施高萍,等.
单位圆外域到任意开挖断面隧洞外域共形映射的计算方法[J].
岩土力学,2014,35(1):175183.
(ZHUJianghong,YANGJianhui,SHIGaoping,etal.
Calculatingmethodforconformalmappingfromexteriorofunitcircletoexteriorofcavernwitharbitraryexcavationcrosssection[J].
RockandSoilMechanics,2014,35(1):175183.
(inChinese))[5]皇甫鹏鹏,伍法权,郭松峰.
基于边界点搜索的洞室外域映射函数求解法[J].
岩石力学,2011,32(5):14181424.
(HUNAGFUPengpeng,WUFaquan,GUOSongfeng.
Anewmethodforcalculatingmappingfunctionofexternalareaofcavernwitharbitraryshapebasedonsearchingpointsonboundary[J].
RockandSoilMechanics,2011,32(5):14181424.
(inChinese))[6]朱大勇,钱七虎,周早生.
复杂形状洞室映射函数的新解法[J].
岩石力学与工程学报,1999,18(3):279282.
(ZHUDayong,QIANQihu,ZHOUZaosheng.
Newmethodforcalculatingmappingfunctionofopeningwithcomplexshape[J].
ChineseJournalofRockMechanicsandEngineering,1999,18(3):279282.
(inChinese))[7]王润富.
一种保角映射法及其微机实现[J].
河海大学学报,1991,19(1):8690.
(WANGRunfu.
Amethodofconformalmappinganditscomputerimplementation[J].
JournalofHohaiUniversity,1991,19(1):8690.
(inChinese))[8]徐趁肖,朱衡君,齐红元.
复杂边界单连通域共形映射解析建模研究[J].
工程数学学报,2002,19(4):135138.
(XUChenxiao,ZHUHengjun,QIHongyuan.
Analyticallymodelingofcomplicatedboundarysimplyconnectedregionconformalmapping[J].
JournalofEngineeringMathematics,2002,19(4):135138.
(inChinese))[9]王志良,申林方,姚激.
浅埋隧道围岩应力场的计算复变函数求解法[J].
岩土力学,2010,31(1):8690.
(WANGZhiliang,SHENLinfang,YAOJi.
Calculationofstressfieldinsurroundingrocksofshallowtunnelusingcomputationalfunctionofcomplexvariablemethod[J].
RockandSoilMechanics,2010,31(1):8690.
(inChinese))[10]王振武,牛铮铮,冯秀苓.
地下矩形洞室应力分布的复变函数解[J].
北华航天工业学院学报,2010,20(4):8690.
(WANGZhenwu,NIUZhengzheng,FENGXiuling.
Asemianalyticalelasticstresssolutionforperimeterstressesofrocksaroundarectangular[J].
JournalofNorthChinaInstituteofAerospaceEngineering,2010,20(4):8690.
(inChinese))[11]李明,茅献彪.
基于复变函数的矩形巷道围岩应力与变形粘弹性分析[J].
力学季刊,2011,32(2):195202.
(LIMing,MAOXianbiao.
Basedonthecomplexvariablefunctionsofrectangularroadwaysurroundingrockstressanddeformationviscoelasticanalysis[J].
ChineseQuarterlyofMechanics,2011,32(2):195202.
(inChinese))[12]袁林,高召宁,孟祥瑞.
基于复变函数法的矩形巷道应力集中系数黏弹性分析[J].
煤矿安全,2013,44(2):196200.
(YUANLin,GAOZhaoning,MENGXiangrui.
Viscoelasticanalysisof68王玉风姬安召崔建斌stressconcentrationcoefficientinrectangularroadwaybasedoncomplexvariablefunction[J].
SafetyinCoalMines,2013,44(2):196200.
(inChinese))[13]施高萍,祝江鸿,李保海,等.
矩形巷道孔边应力的弹性分析[J].
岩土力学,2014,35(9):25872601.
(SHIGaoping,ZHUJianghong,LIBaohai,etal.
Elasticanalysisofholeedgestressofrectangularroadway[J].
RockandSoilMechanics,2014,35(9):25872601.
(inChinese))[14]陈凯,唐治,崔乃鑫,等.
矩形巷道围岩应力解析解[J].
安全与环境学报,2015,15(3):124128.
(CHENKai,TANGZhi,CUINaixin,atel.
Analyticalsolutionofrectangularroadwaysurroundingrockstress[J].
JournalofSafetyandEnvironment,2015,15(3):124128.
(inChinese))[15]何峰,唐治,朱小景,等.
矩形巷道围岩应力分布特征[J].
数学的实践与认识,2015,45(20):128134.
(HEFeng,TANGZhi,ZHUXiaojing,etal.
Stressdistributioncharacteristicsofrectangularroadwaysurroundingrocks[J].
MathematicsinPracticeandTheory,2015,45(20):128134.
(inChinese))[16]赵凯,刘长武,张国良.
用弹性力学的复变函数法求解矩形硐室周边应力[J].
采矿与安全工程学报,2007,24(3):361365.
(ZHAOKai,LIUChangwu,ZHANGGuoliang.
Solutionforperimeterstressesofrocksaroundarectangularchamberusingthecomplexfunctionofelasticmechanics[J].
JournalofMiningandSafetyEngineering,2007,24(3):361365.
(inChinese))[17]HOWELLLH,TREFETHENLN.
AmodifiedSchwarzChristoffeltransformationforelongatedregions[J].
SocietyforIndustrialandAppliedMathematics,1990,11(5):928949.
[18]拉夫连季耶夫МА,沙巴特БВ.
复变函数论方法[M].
6版.
施祥林,夏定中,吕乃刚,译.
北京:高等教育出版社,2006.
(ЛАВРЕНТЬЕВМА,ШАБАТБВ.
MethodsoftheTheoryofComplexFunction[M].
6thed.
SHIXiangling,XIADingzhong,LNaigang,transl.
Beijing:HigherEducationPress,2006.
(Chineseversion))[19]COSTAMAGNAE.
AnewapproachtostandardSchwarzChristoffelformulacalculations[J].
MicrowaveandOpticalTechnologyLetters,2002,32(3):196199.
[20]DRISCOLLTA.
Algorithm843:improvementstotheSchwarzChristoffeltoolboxforMATLAB[J].
ACMTransactionsonMathematicalSoftware,2005,31(2):239251.
[21]崔建斌,姬安召,鲁洪江,等.
SchwarzChristoffel变换数值解法[J].
山东大学学报(理学版),2016,51(4):104111.
(CUIJianbin,JIAnzhao,LUHongjiang,etal.
NumericalsolutionofSchwarzChristoffeltransform[J].
JournalofShandongUniversity(NaturalScience),2015,51(4):104111.
(inChinese))[22]崔建斌,姬安召,王玉风,等.
单位圆到任意多边形区域的SchwarzChristoffel变换数值解法[J].
浙江大学学报(理学版),2017,44(2):161167.
(CUIJianbin,JIAnzhao,WANGYufeng,etal.
NumericalsolutionmethodforSchwarzChristoffeltransformfromunitcircletoarbitrarypolygonarea[J].
JournalofZhejiangUniversity(ScienceEdition),2017,44(2):161167.
(inChinese))[23]NATARAJANS,BORDASS,MAHAPATRADR.
NumericalintegrationoverarbitrarypolygonaldomainsbasedonSchwarzChristoffelconformalmapping[J].
InternationalJournalforNumericalMethodsinEngineering,2009,80(1):103134.
[24]CROWDYD.
TheSchwarzChristoffelmappingtoboundedmultiplyconnectedpolygonaldomains[J].
ProceedingsMathematicalPhysical&EngineeringScience,2005,146(2061):26532678.
[25]刘浩.
大规模非线性方程组和无约束优化方法研究[D].
博士学位论文.
南京:南京航空航天大78矩形到任意多边形区域的SchwarzChristoffel变换数值解法学,2008.
(LIUHao.
Researchonmethodsforlargescalenonlinearequationsandunconstrainedoptimization[D].
PhDThesis.
Nanjing:NanjingUniversityofAeronauticsandAstronautics,2008.
(inChinese))[26]姚征.
椭圆函数的精细积分改进算法[J].
数值计算与计算机应用,2008,29(4):251260.
(YAOZheng.
Theimprovedpreciseintegrationmethodforellipticfunctions[J].
JournalonNumericalMethodsandComputerApplications,2008,29(4):251260.
(inChinese))[27]ABRAMOWITZM,STEGUNIA.
HandbookofMathematicalFunctionsWithFormulas,Graphs,andMathematicalTables[M].
WashingtonDC:DoverPublications,1996.
NumericalSolutionofSchwarzChristoffelTransformationFromRectanglestoArbitraryPolygonalDomainsWANGYufeng,JIAnzhao,CUIJianbin(SchoolofEnergyEngineering,LongdongUniversity,Qingyang,Gansu745000,P.
R.
China)Abstract:WiththeSchwarzChristoffeltransformationmethod,amathematicalmodelofconformalmappingfrompolygonaldomainstostripdomainswasestablished.
Forconstraintconditionsandsingularintegralproblemsinthemodel,thereciprocaltransformationbetweencomplexparametersandrealparameterswasconductedbasedontheRiemannprinciple,whicheliminatesconstraintconditionsofthenonlinearsystem.
Bymeansofreasonableintegrationpaths,thesingularintegralinthemodelwastransformedintotheGaussJacobiintegral,andthenonlinearsystemmodelwassolvedwiththeLevenbergMarquardtalgorithm.
Accordingtothefirstclassellipticfunctioncharacteristics,themathematicalmodelofconformalmappingfromrectangulardomainstostripdomainswasbuilt,andtherelationshipbetweentherectangularboundaryandthestripboundarywasobtainedthroughcalculationofthecomplexparameterellipticfunction.
Atlast,an8pointpolygonaldomainanda27pointirregularstripdomainwerecalculatedtomaptheirregularcloseddomainboundarytotherectangulardomainboundary.
Theorthogonalgridintherectangulardomainstillmeetsorthogonalityinthepolygonaldomainaftermapping.
Thisstudyprovidesafoundationfornumericalcalculationofmappingfromirregulardomainstoregularones.
Keywords:SchwarzChristoffeltransformation;complexparameterellipticfunction;LevenbergMarquardtalgorithm;rectangulardomain;polygonaldomain88王玉风姬安召崔建斌引用本文/Citethispaper:王玉风,姬安召,崔建斌.
矩形到任意多边形区域的SchwarzChristoffel变换数值解法[J].
应用数学和力学,2019,40(1):7588.
WANGYufeng,JIAnzhao,CUIJianbin.
NumericalsolutionofSchwarzChristoffeltransformationfromrectanglestoarbitrarypolygonaldomains[J].
AppliedMathematicsandMechanics,2019,40(1):7588.
- 文章编号:10000887(2019)01007514相关文档
- 会议室崔建斌
- 西安文理学院外国语学院第十八周党政主要工作安排
- 西安文理学院外国语学院第二周党政主要工作安排
- 驾驶人崔建斌
- 本公司崔建斌
- 新星崔建斌
新网,域名7月盛夏1核心2G内存.COM域名仅19.9元/首年,主机9.9元/月,企业邮箱0元体验
新网好不好?新网域名便宜吗?新网怎么样?新网是国内老牌知名域名注册商,企业正规化运营,资质齐全,与阿里云万网和腾讯云DNSPOD同为国内服务商巨头。近日新网发布了最新的七月放价季优惠活动,主要针对域名、云主机、企业邮箱、SSL证书等多款云产品推送了超值的优惠,其中.com顶级域名仅19.9元/首年,.cn域名仅16元/首年,云主机1核心2G内存3Mbps带宽仅9.9元/月,企业邮箱更是免费送1年,...

DMIT$10.9/月,日本VPS/三网直连/1核1.5G内存/20GB存储/1Gbps端口
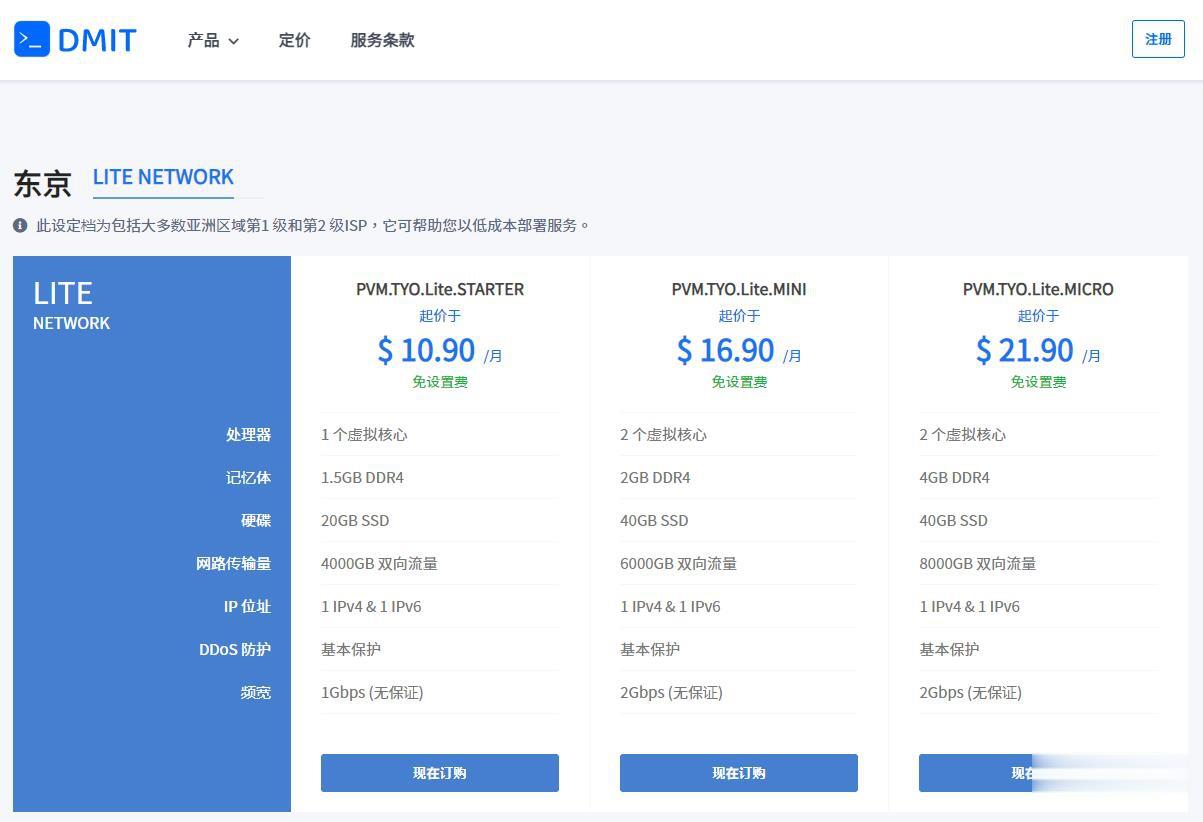
优惠码年付一次性5折优惠码:TYO-Lite-Open-Beta-1y-50OFF永久8折优惠码:TYO-Lite-Open-Beta-Recur-20OFF日本vpsCPU内存SSD流量带宽价格购买1核1.5G20 GB4 TB1Gbps$10.9/月购买2核2 G40 GB6 TB1Gbps$16.9/月购买2核4 G60 GB8 TB1Gbps$21.9/月购买4核4 G80 GB12 TB...
CheapWindowsVPS$4.5/月,美国VPS/免费Windows系统/1Gbps不限流量/,可选美洲、欧洲、亚洲等8大机房
国外商家提供Windows系统的并不常见,CheapWindowsVPS 此次提供的 2 款 VPS 促销套餐,提供 5 折永久优惠码,优惠后月付 4.5 美元起,价格还是挺诱人的,VPS 不限流量,接入 1Gbps 带宽,8 个机房皆可选,其中洛杉矶机房还提供亚洲优化网络供选择,操作系统有 Windows 10 专业版、2012 R2、2016、Linux等。Cheap Windows VPS是...
崔建斌为你推荐
-
关键字数据库:什么是关键字?巫正刚阿迪三叶草彩虹板鞋的鞋带怎么穿?详细点,最后有图解。高分求www.522av.com现在怎样在手机上看AV斗城网女追男有多易?喜欢你,可我不知道你喜不喜欢我!!平安夜希望有他陪我过lcoc.top日本Ni-TOP是什么意思?www.ijinshan.com驱动人生是电脑自带的还是要安装啊!?在哪里呢?没有找到555sss.com不能在线播放了??555javlibrary.com大家有没有在线图书馆WWW。QUESTIA。COM的免费帐号www.k8k8.com谁能给我几个街污网站我去自己学汴京清谈汴京平,众争趋赀货,璋独无所取,惟载书数千卷而还什么意思