plicitmail.aliyun.com
mail.aliyun.com 时间:2021-04-06 阅读:()
Changetal.
JournalofInequalitiesandApplications(2018)2018:124https://doi.
org/10.
1186/s13660-018-1713-zRESEARCHOpenAccessThemodiedproximalpointalgorithminHadamardspacesShih-senChang1,2,LinWang2*,Ching-FengWen3andJianQiangZhang2*Correspondence:Wl64mail@aliyun.
com2CollegeofStatisticsandMathematics,YunnanUniversityofFinanceandEconomics,Kunming,ChinaFulllistofauthorinformationisavailableattheendofthearticleAbstractThepurposeofthispaperistoproposeamodiedproximalpointalgorithmforsolvingminimizationproblemsinHadamardspaces.
Wethenprovethatthesequencegeneratedbythealgorithmconvergesstrongly(convergenceinmetric)toaminimizerofconvexobjectivefunctions.
TheresultsextendseveralresultsinHilbertspaces,Hadamardmanifoldsandnon-positivecurvaturemetricspaces.
MSC:47H09;47J25Keywords:Hadamardspace;CAT(0)space;Moreau–Yosidaresolvent;Implicititerativerule;Proximalpointalgorithm;Variationalinequality1IntroductionLet(X,d)beametricspaceandf:Xbeaproperandconvexfunction.
Oneofthemostimportantproblemsinconvexanalysisistheconvexoptimizationproblemtondx∈Xsuchthatfx=miny∈Xf(y).
Wedenotebyargminy∈Xf(y)thesetofminimizersoffinX.
Convexoptimizationprovidesuswithalgorithmsforsolvingavarietyofproblemswhichmayappearinsciencesandengineering.
Oneofthemostpopularmethodsforapproxima-tionofaminimizerofaconvexfunctionistheproximalpointalgorithm(PPA),whichwasintroducedbyMartinet[1]andRockafellar[2]inHilbertspaces.
Indeed,letfbeaproper,convexandlowersemicontinuousfunctiononarealHilbertspaceHwhichattainsitsminimum.
ThePPAisdenedbyx1∈Handxn+1=argminy∈Hf(y)+12λny–xn2,λn>0,n≥1.
Itwasprovedthatthesequence{xn}convergesweaklytoaminimizeroffprovided∞n=1λn=∞.
However,asshownbyGüer[3],thePPAdoesnotnecessarilyconvergesstrongly(i.
e.
,convergenceinmetric)ingeneral.
Forgettingthestrongconvergenceoftheproximalpointalgorithm,Xu[4]andKamimuraandTakahashi[5]introducedaHalpern-typeregularizationoftheproximalpointalgorithminHilbertspaces.
TheyprovedtheTheAuthor(s)2018.
ThisarticleisdistributedunderthetermsoftheCreativeCommonsAttribution4.
0InternationalLicense(http://creativecommons.
org/licenses/by/4.
0/),whichpermitsunrestricteduse,distribution,andreproductioninanymedium,pro-videdyougiveappropriatecredittotheoriginalauthor(s)andthesource,providealinktotheCreativeCommonslicense,andindicateifchangesweremade.
Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page2of10strongconvergenceofHalpernproximalpointalgorithmundersomecertainconditionsontheparameters.
Recently,manyconvergenceresultsbyPPAforsolvingoptimizationproblemshavebeenextendedfromtheclassicallinearspacessuchasEuclideanspaces,HilbertspacesandBa-nachspacestothesettingofmanifolds[6–9].
Theminimizersoftheobjectiveconvexfunctionalsinthespaceswithnonlinearityplayacrucialroleinthebranchofanalysisandgeometry.
In2013,Baák[10]introducedthePPAinaCAT(0)space(X,d)asfollows:x1∈Xandxn+1=argminy∈Xf(y)+12λnd(y,xn)2,λn>0,n≥1.
BasedontheconceptofFejérmonotonicity,itwasshownthatiffhasaminimizerand∞n=1λn=∞,then{xn}-convergestoitsminimizer(seealso[11]).
In2015Cholamjiak[12]presentedthemodiedPPAbyHalperniterationandthenprovestrongconvergencetheoremintheframeworkofCAT(0)spaces.
Veryrecently,Khatibzadehetal.
[13]presentedaHalpern-typeregularizationoftheproximalpointalgorithm,undersuitableconditionstheyprovedthatthesequencegen-eratedbythealgorithmconvergesstronglytoaminimizeroftheconvexfunctioninHadamardspaces.
Itistherefore,inthiswork,tocontinuealongtheselinesandbyusingtheviscosityim-plicitrulestointroducethemodiedPPAinHadamardspaceforsolvingminimizationproblems.
Weprovethatthesequencegeneratedbythealgorithmconvergesstronglytoaminimizerofconvexobjectivefunctions.
TheresultspresentedinthepaperextendandimprovethemainresultsofMartinet[1],Rockafellar[2]Baák[10],Cholamjiak[12],Xu[4],KamimuraandTakahashi[5],Khatibzadehetal.
[13,Theorem4.
4].
2PreliminariesandlemmasInordertoprovethemainresults,thefollowingnotions,lemmasandconclusionswillbeneeded.
Let(X;d)beametricspaceandletx,y∈X.
Ageodesicpathjoiningxtoyisanisometryc:[0,d(x;y)]→Xsuchthatc(0)=x,c(d(x;y))=y.
Theimageofageodesicpathjoiningxtoyiscalledageodesicsegmentbetweenxandy.
Themetricspace(X;d)issaidtobeageodesicspace,ifeverytwopointsofXarejoinedbyageodesic,andXissaidtobeuniquelygeodesicspace,ifthereisexactlyonegeodesicjoiningxandyforeachx,y∈X.
Ageodesicspace(X;d)isaCAT(0)space,ifandonlyifd2(1–t)xty,z≤(1–t)d2(x,z)+td2(y,z)–t(1–t)d2(x,y)(2.
1)forallx,y,z∈Xandallt∈[0,1][14].
ItiswellknownthatanycompleteandsimplyconnectedRiemannianmanifoldhavingnon-positivesectionalcurvatureisaCAT(0)space.
OtherexamplesofCAT(0)spacesin-cludepre-Hilbertspaces[15],R-trees,Euclideanbuildings[16].
AcompleteCAT(0)spaceisoftencalledaHadamardspace.
Wewrite(1–t)xtyfortheuniquepointzinthegeodesicsegmentjoiningfromxtoysuchthatd(x,z)=td(x,y)andd(y,z)=(1–t)d(x,y).
Wealsodenoteby[x,y]thegeodesicsegmentjoiningxtoy,thatis,[x,y]={(1–t)xty:0≤t≤1}.
AsubsetCofaCAT(0)spaceisconvexif[x,y]Cforallx,y∈C.
Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page3of10ForathoroughdiscussionofCAT(0)spaces,somefundamentalgeometricpropertiesandimportantconclusions,werefertoBridsonandHaeiger[15,16].
Thefollowinglemmasplayanimportantroleinprovingourmainresults.
Lemma2.
1([17])LetXbeaCAT(0)space.
Forallx,y,z∈Xandt,s∈[0,1],wehavethefollowing:(1)d(tx(1–t)y,z)≤td(x,z)+(1–t)d(y,z);(2)d(tx(1–t)y,sx(1–s)y)=|t–s|d(x,y);(3)d(tx(1–t)y,tu(1–t)w)≤td(x,u)+(1–t)d(y,w).
BergandNikolaev[18]introducedthefollowingconceptofquasi-linearizationinCAT(0)spaceX:Denoteapair(a,b)∈X*Xby→abandcallitavector.
Quasi-linearizationinCAT(0)spaceXisdenedasamapping·,·:(X*X)*(X*X)→Rsuchthat→ab,→cd=12d2(a,d)+d2(b,c)–d2(a,c)–d2(b,d)(2.
2)foralla,b,c,d∈X.
WesaythatXsatisestheCauchy–Schwarzinequalityif→ab,→cd≤d(a,b)d(c,d),a,b,c,d∈X.
(2.
3)Itiswellknown[18,Corollary3]thatageodesicallyconnectedmetricspaceisaCAT(0)spaceifandonlyifitsatisestheCauchy–Schwarzinequality.
Byusingquasi-linearization,AhmadiKakavandi[19]provedthat{xn}-convergestox∈Xifandonlyiflimsupn→∞→xxn,→xy≤0,y∈X.
(2.
4)LetCbeanonemptyclosedconvexsubsetofacompleteCAT(0)spaceX(i.
e.
,aHadamardspace).
ThemetricprojectionPC:X→Cisdenedbyu=PC(x)d(u,x)=infd(y,x):y∈C,x∈X.
(2.
5)Lemma2.
2([18])LetCbeanonemptyclosedandconvexsubsetofaHadamardspaceX,x∈Xandu∈C.
Thenu=PC(x)ifandonlyif→yu,→ux≥0,y∈C.
(2.
6)LetCbeaconvexsubsetofaCAT(0)spaceX.
Recallthatafunctionf:Cissaidtobeconvexif,foranygeodesicγ:[a,b]→C,thefunctionfγisconvex,i.
e.
,fγ[a,b]:=f(1–t)atb≤(1–t)f(a)+tf(b),a,b∈Candt∈(0,1).
(2.
7)Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page4of10Someimportantexamplesofconvexfunctionscanbefoundin[15].
Forr>0,denetheMoreau–YosidaresolventoffinCAT(0)spacesasJr(x)=argminy∈Xf(y)+12rd2(y,x)(2.
8)forallx∈X(see[20]).
ThemappingJriswelldenedforallr>0(see[20]).
Lemma2.
3([11])Let(X,d)beaHadamardspaceandf:Xbeaproper,convexandlowersemicontinuousfunction.
Then,foreveryr>0:(1)theresolventJrisrmlynonexpansive,thatis,d(Jrx,Jry)≤d(1–λ)xλJrx,(1–λ)yλJryforallx,y∈Xandforallλ∈(0,1);(2)thesetFix(Jr)ofxedpointsoftheresolventJrassociatedwithfcoincideswiththesetargminy∈Xf(y)ofminimizersoff.
Remark2.
4Everyrmlynonexpansivemappingisnonexpansive.
HenceJrisanonexpan-sivemapping.
Lemma2.
5([21])LetXbeaCAT(0)space,CbeanonemptyclosedandconvexsubsetofXandT:C→Cbeanonexpansivemapping.
Foranycontractionφ:C→Candt∈(0,1),letxt∈Cbetheuniquexedpointofthecontractionx→tf(x)(1–t)Tx,i.
e.
,xt=tφ(xt)(1–t)Txt.
(2.
9)Then{xt}convergestronglyast→0toapointxsuchthatx=PFix(T)φx,whichistheuniquesolutiontothefollowingvariationalinequality:→xφx,→xx≥0,x∈Fix(T).
(2.
10)Lemma2.
6([22])Let{an}beasequenceofnonnegativerealnumberssatisfyingan+1≤(1–γn)an+δn(2.
11)foralln≥0,where{γn}isasequencein(0,1)and{δn}isasequenceinRsuchthat:(a)∞n=1γn=∞;(b)limsupn→∞δnγn≤0or∞n=1|δn|0,andf:Cbeaproper,convexandlowersemicontinuousfunctionwithFix(Jr)=,whereJristheMoreau–YosidaresolventoffdenedbyJr(x)=argminy∈Cf(y)+12rd2(y,x).
Letφ:C→Cbeacontractionwiththecontractivecoecientk∈[0,1)and,forarbitraryinitialpointx0∈C,let{xn}betheimplicititerativesequencegeneratedbyxn+1=αnφ(xn)(1–αn)Jrβnxn(1–βn)xn+1(3.
1)foralln≥0,whereαn∈(0,1),βn∈[0,1]satisfythefollowingconditions:(a)limn→∞αn=0;(b)∞n=0αn=∞;(c)|αn–αn–1|α2n→0asn→∞.
Thenthesequence{xn}convergesstronglytox=PFix(Jr)φ(x),whichisaxedpointofJr(therefore,byLemma2.
3,itisaminimizeroff)anditisalsoasolutionofthefollowingvariationalinequality:→xφx,→xx≥0,x∈Fix(Jr).
ProofWedividetheproofintofoursteps.
Step1.
First,weprovethatthesequence{xn}denedby(3.
1)iswelldened.
Infact,forarbitrarilygivenu∈C,themappingx→Tu(x):=αφ(u)(1–α)Jrβu(1–β)x,x∈C,andα∈(0,1),β∈[0,1](3.
2)isacontractionwiththecontractiveconstant1–α.
Indeed,itfollowsfromLemma2.
1andLemma2.
3that,foranyx,y∈C,d(Tux,Tuy)=dαφ(u)(1–α)Jrβu(1–β)x,αφ(u)(1–α)Jrβu(1–β)y≤(1–α)dJrβu(1–β)x,Jrβu(1–β)y≤(1–α)(1–β)d(x,y)≤(1–α)d(x,y).
ThisimpliesthatthemappingTu:C→Cisacontraction.
Hencetheimplicititerativesequence{xn}denedby(3.
1)iswelldened.
Step2.
Next,weprovethat{xn}isbounded.
Infact,takingp∈Fix(Jr),wehaved(xn+1,p)=dαnφ(xn)(1–αn)Jrβnxn(1–βn)xn+1,p≤αndφ(xn),p+(1–αn)dJrβnxn(1–βn)xn+1,pChangetal.
JournalofInequalitiesandApplications(2018)2018:124Page6of10≤αndφ(xn),φ(p)+dφ(p),p+(1–αn)dJrβnxn(1–βn)xn+1,Jr(p)≤αnkd(xn,p)+αndφ(p),p+(1–αn)βnd(xn,p)+(1–βn)d(xn+1,p),whichimpliesthatd(xn+1,p)≤1αn+(1–αn)βnαnk+(1–αn)βnx(xn,p)+αndφ(p),p=1–αn(1–k)αn+(1–αn)βnd(xn,p)+αn(1–k)d(φ(p),p)(αn+(1–αn)βn)(1–k)≤maxd(xn,p),d(φ(p),p)1–k.
Byinduction,wecanprovethatd(xn,p)≤maxd(x0,p),d(φ(p),p)1–kforalln≥0.
Thisimpliesthat{xn}isboundedandsoare{φ(xn)}and{Jr(βnxn(1–βn)xn+1)}.
Step3.
Next,weprovethatthesequence{xn}convergesstronglytosomepointinFix(Jr).
Lettingzn=αnφ(zn)(1–αn)Jrzn(3.
3)foralln≥0.
ByLemma2.
5,thesequence{zn}convergesstronglyasn→∞toapointx=PFix(Jr)φ(x),whichistheuniquesolutiontothefollowingvariationalinequality:→xφx,→xx≥0,x∈Fix(Jr).
(3.
4)Ontheotherhand,itfollowsfrom(3.
1),Lemma2.
3andLemma2.
1thatd(xn+1,zn)=dαnφ(xn)(1–αn)Jrβnxn(1–βn)xn+1,αnφ(zn)(1–αn)Jrzn≤αndφ(xn),φ(zn)+(1–αn)dJrβnxn(1–βn)xn+1,Jrzn≤αnkd(xn,zn)+(1–αn)βnd(xn,zn)+(1–βn)d(xn+1,zn),whichimpliesthatd(xn+1,zn)≤αnk+(1–αn)βnαn+(1–αn)βnd(xn,zn)=1–αn(1–k)αn+(1–αn)βnd(xn,zn)≤1–αn(1–k)d(xn,zn–1)+d(zn–1,zn)≤1–αn(1–k)d(xn,zn–1)+d(zn–1,zn).
(3.
5)Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page7of10InordertouseLemma2.
6,itshouldbeprovedthatlimsupn→∞d(zn–1,zn)αn(1–k)≤0.
(3.
6)Infact,byLemma2.
1andLemma2.
3,wehaved(zn,zn–1)=dαnφ(zn)(1–αn)Jrzn,αn–1φ(zn–1)(1–αn–1)Jrzn–1≤dαnφ(zn)(1–αn)Jrzn,αnφ(zn)(1–αn)Jrzn–1+dαnφ(zn)(1–αn)Jrzn–1,αnφ(zn–1)(1–αn)Jrzn–1+dαnφ(zn–1)(1–αn)Jrzn–1,αn–1φ(zn–1)(1–αn–1)Jrzn–1≤(1–αn)d(Jrzn,Jrzn–1)+αndφ(zn),φ(zn–1)+|αn–αn–1|dφ(zn–1),Jrzn–1≤(1–αn)d(zn,zn–1)+αnkd(zn,zn–1)+|αn–αn–1|M,whereM=supn≥1d(φ(zn–1),Jrzn–1),whichimpliesthatd(zn,zn–1)≤1αn(1–k)|αn–αn–1|M.
Bythecondition(c),wehavelimsupn→∞d(zn–1,zn)αn(1–k)≤limsupn→∞|αn–αn–1|Mα2n(1–k)2=0.
Hence(3.
6)isproved.
ByLemma2.
6and(3.
5),itfollowsthatlimn→∞d(xn+1,zn)=0.
Sincezn→x=PFix(Jr)φ(x),thisimpliesthatxn→x∈Fix(Jr).
ByLemma2.
3,x∈argminy∈Cf(y)andxisalsotheuniquesolutionofthevariationalinequality(3.
4).
Thiscompletestheproof.
RemarkAnsimpleexampleofasequence{αn}satisfyingconditions(a)–(c)isgivenby{αn=1/nσ},where00,andf:Cbeaproper,convexandlowersemicontinuousfunctionwithFix(Jr)=,whereJristheMoreau–YosidaresolventoffdenedbyJr(x)=argminy∈Cf(y)+12rd2(y,x).
Letφ:C→Cbeacontractionwiththecontractivecoecientk∈[0,1)and,forarbitraryinitialpointx0∈C,let{xn}bethesequencegeneratedbyxn+1=αnφ(xn)+(1–αn)Jrβnxn+(1–βn)xn+1(3.
8)foralln≥0,whereαn∈(0,1),βn∈[0,1]satisfytheconditions(a)–(c)inTheorem3.
1.
ThentheconclusionsinTheorem3.
1stillhold.
4ApplicationsInthissection,weshallutilizetheresultspresentedinthepapertostudyaclassofinclu-sionproblemsinHilbertspace.
LetHbearealHilbertspaceandf:Hbeaproperandconvexlowersemi-continuousfunction.
Nowweconsiderthefollowinginclusionproblem:tondapointx∈Hsuchthatx∈(f)–1(0),(4.
1)wherefisthesubdierentialoff.
ByFermat'stheorem(seeRockafellar[2]),itiseasytoseethatx∈(f)–1(0)x∈FixJfrfx=miny∈Hf(y),(4.
2)whereJfristheresolventassociatedwithfdenedbyJfr(x):=(I+rf)–1(x),x∈H,r>0,(4.
3)whereIstandsfortheidentitymappingonH.
Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page9of10Wenotethat,forallr>0,theresolventmappingJfrisasingle-valuednonexpansivemapping.
ThereforethefollowingresultcanbeobtainedfromTheorem3.
2immediately.
Theorem4.
1LetHbearealHilbertspace,r>0andf:Hbeaproper,con-vexandlowersemicontinuousfunctionwithFix(Jfr)=.
Letφ:H→Hbeacontractionwiththecontractivecoecientk∈[0,1).
Forarbitraryinitialpointx0∈H,let{xn}bethesequencegeneratedbyxn+1=αnφ(xn)+(1–αn)Jfrβnxn+(1–βn)xn+1,n≥0,(4.
4)whereαn∈(0,1),βn∈[0,1]satisfytheconditions(a)–(c)inTheorem3.
2.
Then{xn}con-vergesstronglytoapointx∈Hwhichisasolutionofinclusionproblem(4.
1),alsoitisaminimizeroffinH.
Similarly,byusingthesamemethodmentionedabove,wecanstudythemonotonevari-ationalinclusionproblem(inshort,(MVIP))inrealHilbertspaceHtondapointx∈Hsuchthat0∈Mx,(4.
5)whereM:H→2Hisamaximalmonotonemapping.
Itiseasytoseethattheproblem(MVIP)(4.
5)isequivalenttondx∈Hsuchthatx∈FixJMr,r>0,whereJMristheresolventassociatedwithMdenedbyJMr(x)=(I+rM)–1(x),x∈H,(4.
6)whichisnonexpansive.
ReplacingtheresolventJfrbytheresolventJMrinTheorem4.
1,wehavethefollowing.
Theorem4.
2LetHbearealHilbertH.
Letr>0,andM:H→2Hbeamaximalmono-tonemappingwithFix(JMr)=.
Letφ:H→Hbeacontractionwiththecontractivecoef-cientk∈[0,1).
Forarbitraryinitialpointx0∈H,let{xn}bethesequencegeneratedbyxn+1=αnφ(xn)+(1–αn)JMrβnxn+(1–βn)xn+1,n≥0,(4.
7)whereαn∈(0,1),βn∈[0,1]satisfytheconditions(a)–(c)inTheorem4.
1.
Then{xn}con-vergesstronglytoapointx∈Hwhichisasolutionofinclusionproblem(4.
5).
AcknowledgementsTheauthorswouldliketoexpresstheirthankstotherefereesandtheeditorsfortheirhelpfulcommentsandadvices.
TherstauthorwassupportedbytheNaturalScienceFoundationofChinaMedicalUniversity,Taiwan,andthesecondauthorwassupportedbytheNationalNaturalSciencesFoundationofChina(GrantNo.
11361070).
CompetinginterestsNoneoftheauthorshaveanycompetinginterestsinthemanuscript.
Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page10of10Authors'contributionsAllauthorscontributedequallyandsignicantlyinwritingthisarticle.
Allauthorsreadandapprovedthenalmanuscript.
Authordetails1CenterforGeneralEducation,ChinaMedicalUniversity,Taichung,Taiwan.
2CollegeofStatisticsandMathematics,YunnanUniversityofFinanceandEconomics,Kunming,China.
3CenterforFundamentalScience,KaohsiungMedicalUniversity,Kaohsiung,Taiwan.
Publisher'sNoteSpringerNatureremainsneutralwithregardtojurisdictionalclaimsinpublishedmapsandinstitutionalaliations.
Received:10December2017Accepted:10May2018References1.
Martinet,B.
:Régularisationd'inéquationsvariationnellesparapproximationssuccessives.
Rev.
Fr.
Inform.
Rech.
Opér.
4,154–158(1970)2.
Rockafellar,T.
:Monotoneoperatorsandtheproximalpointalgorithm.
SIAMJ.
ControlOptim.
14,877–898(1976)3.
Güler,O.
:Ontheconvergenceoftheproximalpointalgorithmforconvexminimization.
SIAMJ.
ControlOptim.
29,403–419(1991)4.
Xu,H.
K.
:Iterativealgorithmsfornonlinearoperators.
J.
Lond.
Math.
Soc.
66,240–256(2002)5.
Kamimura,S.
,Takahashi,W.
:ApproximatingsolutionsofmaximalmonotoneoperatorsinHilbertspaces.
J.
Approx.
Theory106,226–240(2000)6.
Ferreira,O.
P.
,Oliveira,P.
R.
:ProximalpointalgorithmonRiemannianmanifolds.
Optimization51,257–270(2002)7.
Li,C.
,López,G.
,Martín-Márquez,V.
:MonotonevectoreldsandtheproximalpointalgorithmonHadamardmanifolds.
J.
Lond.
Math.
Soc.
79,663–683(2009)8.
PapaQuiroz,E.
A.
,Oliveira,P.
R.
:ProximalpointmethodsforquasiconvexandconvexfunctionswithBregmandistancesonHadamardmanifolds.
J.
ConvexAnal.
16,49–69(2009)9.
Wang,J.
H.
,López,G.
:ModiedproximalpointalgorithmsonHadamardmanifolds.
Optimization60,697–708(2011)10.
Baˇcák,M.
:Theproximalpointalgorithminmetricspaces.
Isr.
J.
Math.
194,689–701(2013)11.
Ariza-Ruiz,D.
,Leustean,L.
,López,G.
:Firmlynonexpansivemappingsinclassesofgeodesicspaces.
Trans.
Am.
Math.
Soc.
366,4299–4322(2014)12.
Cholamjiak,P.
:ThemodiedproximalpointalgorithminCAT(0)spaces.
Optim.
Lett.
9,1401–1410(2015)13.
Khatibzadeh,H.
,Mohebbi,V.
,Ranjbar,S.
:Newresultsontheproximalpointalgorithminnonpositivecurvaturemetricspaces.
Optimization66(7),1191–1199(2017)14.
Bruhat,M.
,Tits,J.
:Groupesréductifssuruncorpslocal.
I.
Donnéesradiciellesvaluées.
Publ.
Math.
Inst.
HautestudesSci.
41,5–251(1972)15.
Bridson,M.
R.
,Haeiger,A.
:MetricSpacesofNon-positiveCurvature.
GrundlehrenderMathematischenWissenschaften,vol.
319.
Springer,Berlin(1999)16.
Brown,K.
S.
:Buildings.
Springer,NewYork(1989)17.
Dhompongsa,S.
,Panyanak,B.
:On-convergencetheoremsinCAT(0)spaces.
Comput.
Math.
Appl.
56,2572–2579(2008)18.
Berg,I.
D.
,Nikolaev,I.
G.
:QuasilinearizationandcurvatureofAlexandrovspaces.
Geom.
Dedic.
133,195–218(2008)19.
Ahmadi,P.
,Khatibzadeh,H.
:OntheconvergenceofinexactproximalpointalgorithmonHadamardmanifolds.
Taiwan.
J.
Math.
18,419–433(2014)20.
Jost,J.
:NonpositiveCurvature:GeometricandAnalyticAspects.
LecturesinMathematicsETHZürich.
Birkhuser,Basel(1997)21.
Wangkeeree,R.
,Preechasilp,P.
:ViscosityapproximationmethodsfornonexpansivemappingsinCAT(0)spaces.
J.
Inequal.
Appl.
2013,ArticleID93(2013)22.
Xu,H.
K.
:Iterativealgorithmsfornonlinearoperators.
J.
Lond.
Math.
Soc.
66,240–256(2002)
JournalofInequalitiesandApplications(2018)2018:124https://doi.
org/10.
1186/s13660-018-1713-zRESEARCHOpenAccessThemodiedproximalpointalgorithminHadamardspacesShih-senChang1,2,LinWang2*,Ching-FengWen3andJianQiangZhang2*Correspondence:Wl64mail@aliyun.
com2CollegeofStatisticsandMathematics,YunnanUniversityofFinanceandEconomics,Kunming,ChinaFulllistofauthorinformationisavailableattheendofthearticleAbstractThepurposeofthispaperistoproposeamodiedproximalpointalgorithmforsolvingminimizationproblemsinHadamardspaces.
Wethenprovethatthesequencegeneratedbythealgorithmconvergesstrongly(convergenceinmetric)toaminimizerofconvexobjectivefunctions.
TheresultsextendseveralresultsinHilbertspaces,Hadamardmanifoldsandnon-positivecurvaturemetricspaces.
MSC:47H09;47J25Keywords:Hadamardspace;CAT(0)space;Moreau–Yosidaresolvent;Implicititerativerule;Proximalpointalgorithm;Variationalinequality1IntroductionLet(X,d)beametricspaceandf:Xbeaproperandconvexfunction.
Oneofthemostimportantproblemsinconvexanalysisistheconvexoptimizationproblemtondx∈Xsuchthatfx=miny∈Xf(y).
Wedenotebyargminy∈Xf(y)thesetofminimizersoffinX.
Convexoptimizationprovidesuswithalgorithmsforsolvingavarietyofproblemswhichmayappearinsciencesandengineering.
Oneofthemostpopularmethodsforapproxima-tionofaminimizerofaconvexfunctionistheproximalpointalgorithm(PPA),whichwasintroducedbyMartinet[1]andRockafellar[2]inHilbertspaces.
Indeed,letfbeaproper,convexandlowersemicontinuousfunctiononarealHilbertspaceHwhichattainsitsminimum.
ThePPAisdenedbyx1∈Handxn+1=argminy∈Hf(y)+12λny–xn2,λn>0,n≥1.
Itwasprovedthatthesequence{xn}convergesweaklytoaminimizeroffprovided∞n=1λn=∞.
However,asshownbyGüer[3],thePPAdoesnotnecessarilyconvergesstrongly(i.
e.
,convergenceinmetric)ingeneral.
Forgettingthestrongconvergenceoftheproximalpointalgorithm,Xu[4]andKamimuraandTakahashi[5]introducedaHalpern-typeregularizationoftheproximalpointalgorithminHilbertspaces.
TheyprovedtheTheAuthor(s)2018.
ThisarticleisdistributedunderthetermsoftheCreativeCommonsAttribution4.
0InternationalLicense(http://creativecommons.
org/licenses/by/4.
0/),whichpermitsunrestricteduse,distribution,andreproductioninanymedium,pro-videdyougiveappropriatecredittotheoriginalauthor(s)andthesource,providealinktotheCreativeCommonslicense,andindicateifchangesweremade.
Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page2of10strongconvergenceofHalpernproximalpointalgorithmundersomecertainconditionsontheparameters.
Recently,manyconvergenceresultsbyPPAforsolvingoptimizationproblemshavebeenextendedfromtheclassicallinearspacessuchasEuclideanspaces,HilbertspacesandBa-nachspacestothesettingofmanifolds[6–9].
Theminimizersoftheobjectiveconvexfunctionalsinthespaceswithnonlinearityplayacrucialroleinthebranchofanalysisandgeometry.
In2013,Baák[10]introducedthePPAinaCAT(0)space(X,d)asfollows:x1∈Xandxn+1=argminy∈Xf(y)+12λnd(y,xn)2,λn>0,n≥1.
BasedontheconceptofFejérmonotonicity,itwasshownthatiffhasaminimizerand∞n=1λn=∞,then{xn}-convergestoitsminimizer(seealso[11]).
In2015Cholamjiak[12]presentedthemodiedPPAbyHalperniterationandthenprovestrongconvergencetheoremintheframeworkofCAT(0)spaces.
Veryrecently,Khatibzadehetal.
[13]presentedaHalpern-typeregularizationoftheproximalpointalgorithm,undersuitableconditionstheyprovedthatthesequencegen-eratedbythealgorithmconvergesstronglytoaminimizeroftheconvexfunctioninHadamardspaces.
Itistherefore,inthiswork,tocontinuealongtheselinesandbyusingtheviscosityim-plicitrulestointroducethemodiedPPAinHadamardspaceforsolvingminimizationproblems.
Weprovethatthesequencegeneratedbythealgorithmconvergesstronglytoaminimizerofconvexobjectivefunctions.
TheresultspresentedinthepaperextendandimprovethemainresultsofMartinet[1],Rockafellar[2]Baák[10],Cholamjiak[12],Xu[4],KamimuraandTakahashi[5],Khatibzadehetal.
[13,Theorem4.
4].
2PreliminariesandlemmasInordertoprovethemainresults,thefollowingnotions,lemmasandconclusionswillbeneeded.
Let(X;d)beametricspaceandletx,y∈X.
Ageodesicpathjoiningxtoyisanisometryc:[0,d(x;y)]→Xsuchthatc(0)=x,c(d(x;y))=y.
Theimageofageodesicpathjoiningxtoyiscalledageodesicsegmentbetweenxandy.
Themetricspace(X;d)issaidtobeageodesicspace,ifeverytwopointsofXarejoinedbyageodesic,andXissaidtobeuniquelygeodesicspace,ifthereisexactlyonegeodesicjoiningxandyforeachx,y∈X.
Ageodesicspace(X;d)isaCAT(0)space,ifandonlyifd2(1–t)xty,z≤(1–t)d2(x,z)+td2(y,z)–t(1–t)d2(x,y)(2.
1)forallx,y,z∈Xandallt∈[0,1][14].
ItiswellknownthatanycompleteandsimplyconnectedRiemannianmanifoldhavingnon-positivesectionalcurvatureisaCAT(0)space.
OtherexamplesofCAT(0)spacesin-cludepre-Hilbertspaces[15],R-trees,Euclideanbuildings[16].
AcompleteCAT(0)spaceisoftencalledaHadamardspace.
Wewrite(1–t)xtyfortheuniquepointzinthegeodesicsegmentjoiningfromxtoysuchthatd(x,z)=td(x,y)andd(y,z)=(1–t)d(x,y).
Wealsodenoteby[x,y]thegeodesicsegmentjoiningxtoy,thatis,[x,y]={(1–t)xty:0≤t≤1}.
AsubsetCofaCAT(0)spaceisconvexif[x,y]Cforallx,y∈C.
Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page3of10ForathoroughdiscussionofCAT(0)spaces,somefundamentalgeometricpropertiesandimportantconclusions,werefertoBridsonandHaeiger[15,16].
Thefollowinglemmasplayanimportantroleinprovingourmainresults.
Lemma2.
1([17])LetXbeaCAT(0)space.
Forallx,y,z∈Xandt,s∈[0,1],wehavethefollowing:(1)d(tx(1–t)y,z)≤td(x,z)+(1–t)d(y,z);(2)d(tx(1–t)y,sx(1–s)y)=|t–s|d(x,y);(3)d(tx(1–t)y,tu(1–t)w)≤td(x,u)+(1–t)d(y,w).
BergandNikolaev[18]introducedthefollowingconceptofquasi-linearizationinCAT(0)spaceX:Denoteapair(a,b)∈X*Xby→abandcallitavector.
Quasi-linearizationinCAT(0)spaceXisdenedasamapping·,·:(X*X)*(X*X)→Rsuchthat→ab,→cd=12d2(a,d)+d2(b,c)–d2(a,c)–d2(b,d)(2.
2)foralla,b,c,d∈X.
WesaythatXsatisestheCauchy–Schwarzinequalityif→ab,→cd≤d(a,b)d(c,d),a,b,c,d∈X.
(2.
3)Itiswellknown[18,Corollary3]thatageodesicallyconnectedmetricspaceisaCAT(0)spaceifandonlyifitsatisestheCauchy–Schwarzinequality.
Byusingquasi-linearization,AhmadiKakavandi[19]provedthat{xn}-convergestox∈Xifandonlyiflimsupn→∞→xxn,→xy≤0,y∈X.
(2.
4)LetCbeanonemptyclosedconvexsubsetofacompleteCAT(0)spaceX(i.
e.
,aHadamardspace).
ThemetricprojectionPC:X→Cisdenedbyu=PC(x)d(u,x)=infd(y,x):y∈C,x∈X.
(2.
5)Lemma2.
2([18])LetCbeanonemptyclosedandconvexsubsetofaHadamardspaceX,x∈Xandu∈C.
Thenu=PC(x)ifandonlyif→yu,→ux≥0,y∈C.
(2.
6)LetCbeaconvexsubsetofaCAT(0)spaceX.
Recallthatafunctionf:Cissaidtobeconvexif,foranygeodesicγ:[a,b]→C,thefunctionfγisconvex,i.
e.
,fγ[a,b]:=f(1–t)atb≤(1–t)f(a)+tf(b),a,b∈Candt∈(0,1).
(2.
7)Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page4of10Someimportantexamplesofconvexfunctionscanbefoundin[15].
Forr>0,denetheMoreau–YosidaresolventoffinCAT(0)spacesasJr(x)=argminy∈Xf(y)+12rd2(y,x)(2.
8)forallx∈X(see[20]).
ThemappingJriswelldenedforallr>0(see[20]).
Lemma2.
3([11])Let(X,d)beaHadamardspaceandf:Xbeaproper,convexandlowersemicontinuousfunction.
Then,foreveryr>0:(1)theresolventJrisrmlynonexpansive,thatis,d(Jrx,Jry)≤d(1–λ)xλJrx,(1–λ)yλJryforallx,y∈Xandforallλ∈(0,1);(2)thesetFix(Jr)ofxedpointsoftheresolventJrassociatedwithfcoincideswiththesetargminy∈Xf(y)ofminimizersoff.
Remark2.
4Everyrmlynonexpansivemappingisnonexpansive.
HenceJrisanonexpan-sivemapping.
Lemma2.
5([21])LetXbeaCAT(0)space,CbeanonemptyclosedandconvexsubsetofXandT:C→Cbeanonexpansivemapping.
Foranycontractionφ:C→Candt∈(0,1),letxt∈Cbetheuniquexedpointofthecontractionx→tf(x)(1–t)Tx,i.
e.
,xt=tφ(xt)(1–t)Txt.
(2.
9)Then{xt}convergestronglyast→0toapointxsuchthatx=PFix(T)φx,whichistheuniquesolutiontothefollowingvariationalinequality:→xφx,→xx≥0,x∈Fix(T).
(2.
10)Lemma2.
6([22])Let{an}beasequenceofnonnegativerealnumberssatisfyingan+1≤(1–γn)an+δn(2.
11)foralln≥0,where{γn}isasequencein(0,1)and{δn}isasequenceinRsuchthat:(a)∞n=1γn=∞;(b)limsupn→∞δnγn≤0or∞n=1|δn|0,andf:Cbeaproper,convexandlowersemicontinuousfunctionwithFix(Jr)=,whereJristheMoreau–YosidaresolventoffdenedbyJr(x)=argminy∈Cf(y)+12rd2(y,x).
Letφ:C→Cbeacontractionwiththecontractivecoecientk∈[0,1)and,forarbitraryinitialpointx0∈C,let{xn}betheimplicititerativesequencegeneratedbyxn+1=αnφ(xn)(1–αn)Jrβnxn(1–βn)xn+1(3.
1)foralln≥0,whereαn∈(0,1),βn∈[0,1]satisfythefollowingconditions:(a)limn→∞αn=0;(b)∞n=0αn=∞;(c)|αn–αn–1|α2n→0asn→∞.
Thenthesequence{xn}convergesstronglytox=PFix(Jr)φ(x),whichisaxedpointofJr(therefore,byLemma2.
3,itisaminimizeroff)anditisalsoasolutionofthefollowingvariationalinequality:→xφx,→xx≥0,x∈Fix(Jr).
ProofWedividetheproofintofoursteps.
Step1.
First,weprovethatthesequence{xn}denedby(3.
1)iswelldened.
Infact,forarbitrarilygivenu∈C,themappingx→Tu(x):=αφ(u)(1–α)Jrβu(1–β)x,x∈C,andα∈(0,1),β∈[0,1](3.
2)isacontractionwiththecontractiveconstant1–α.
Indeed,itfollowsfromLemma2.
1andLemma2.
3that,foranyx,y∈C,d(Tux,Tuy)=dαφ(u)(1–α)Jrβu(1–β)x,αφ(u)(1–α)Jrβu(1–β)y≤(1–α)dJrβu(1–β)x,Jrβu(1–β)y≤(1–α)(1–β)d(x,y)≤(1–α)d(x,y).
ThisimpliesthatthemappingTu:C→Cisacontraction.
Hencetheimplicititerativesequence{xn}denedby(3.
1)iswelldened.
Step2.
Next,weprovethat{xn}isbounded.
Infact,takingp∈Fix(Jr),wehaved(xn+1,p)=dαnφ(xn)(1–αn)Jrβnxn(1–βn)xn+1,p≤αndφ(xn),p+(1–αn)dJrβnxn(1–βn)xn+1,pChangetal.
JournalofInequalitiesandApplications(2018)2018:124Page6of10≤αndφ(xn),φ(p)+dφ(p),p+(1–αn)dJrβnxn(1–βn)xn+1,Jr(p)≤αnkd(xn,p)+αndφ(p),p+(1–αn)βnd(xn,p)+(1–βn)d(xn+1,p),whichimpliesthatd(xn+1,p)≤1αn+(1–αn)βnαnk+(1–αn)βnx(xn,p)+αndφ(p),p=1–αn(1–k)αn+(1–αn)βnd(xn,p)+αn(1–k)d(φ(p),p)(αn+(1–αn)βn)(1–k)≤maxd(xn,p),d(φ(p),p)1–k.
Byinduction,wecanprovethatd(xn,p)≤maxd(x0,p),d(φ(p),p)1–kforalln≥0.
Thisimpliesthat{xn}isboundedandsoare{φ(xn)}and{Jr(βnxn(1–βn)xn+1)}.
Step3.
Next,weprovethatthesequence{xn}convergesstronglytosomepointinFix(Jr).
Lettingzn=αnφ(zn)(1–αn)Jrzn(3.
3)foralln≥0.
ByLemma2.
5,thesequence{zn}convergesstronglyasn→∞toapointx=PFix(Jr)φ(x),whichistheuniquesolutiontothefollowingvariationalinequality:→xφx,→xx≥0,x∈Fix(Jr).
(3.
4)Ontheotherhand,itfollowsfrom(3.
1),Lemma2.
3andLemma2.
1thatd(xn+1,zn)=dαnφ(xn)(1–αn)Jrβnxn(1–βn)xn+1,αnφ(zn)(1–αn)Jrzn≤αndφ(xn),φ(zn)+(1–αn)dJrβnxn(1–βn)xn+1,Jrzn≤αnkd(xn,zn)+(1–αn)βnd(xn,zn)+(1–βn)d(xn+1,zn),whichimpliesthatd(xn+1,zn)≤αnk+(1–αn)βnαn+(1–αn)βnd(xn,zn)=1–αn(1–k)αn+(1–αn)βnd(xn,zn)≤1–αn(1–k)d(xn,zn–1)+d(zn–1,zn)≤1–αn(1–k)d(xn,zn–1)+d(zn–1,zn).
(3.
5)Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page7of10InordertouseLemma2.
6,itshouldbeprovedthatlimsupn→∞d(zn–1,zn)αn(1–k)≤0.
(3.
6)Infact,byLemma2.
1andLemma2.
3,wehaved(zn,zn–1)=dαnφ(zn)(1–αn)Jrzn,αn–1φ(zn–1)(1–αn–1)Jrzn–1≤dαnφ(zn)(1–αn)Jrzn,αnφ(zn)(1–αn)Jrzn–1+dαnφ(zn)(1–αn)Jrzn–1,αnφ(zn–1)(1–αn)Jrzn–1+dαnφ(zn–1)(1–αn)Jrzn–1,αn–1φ(zn–1)(1–αn–1)Jrzn–1≤(1–αn)d(Jrzn,Jrzn–1)+αndφ(zn),φ(zn–1)+|αn–αn–1|dφ(zn–1),Jrzn–1≤(1–αn)d(zn,zn–1)+αnkd(zn,zn–1)+|αn–αn–1|M,whereM=supn≥1d(φ(zn–1),Jrzn–1),whichimpliesthatd(zn,zn–1)≤1αn(1–k)|αn–αn–1|M.
Bythecondition(c),wehavelimsupn→∞d(zn–1,zn)αn(1–k)≤limsupn→∞|αn–αn–1|Mα2n(1–k)2=0.
Hence(3.
6)isproved.
ByLemma2.
6and(3.
5),itfollowsthatlimn→∞d(xn+1,zn)=0.
Sincezn→x=PFix(Jr)φ(x),thisimpliesthatxn→x∈Fix(Jr).
ByLemma2.
3,x∈argminy∈Cf(y)andxisalsotheuniquesolutionofthevariationalinequality(3.
4).
Thiscompletestheproof.
RemarkAnsimpleexampleofasequence{αn}satisfyingconditions(a)–(c)isgivenby{αn=1/nσ},where00,andf:Cbeaproper,convexandlowersemicontinuousfunctionwithFix(Jr)=,whereJristheMoreau–YosidaresolventoffdenedbyJr(x)=argminy∈Cf(y)+12rd2(y,x).
Letφ:C→Cbeacontractionwiththecontractivecoecientk∈[0,1)and,forarbitraryinitialpointx0∈C,let{xn}bethesequencegeneratedbyxn+1=αnφ(xn)+(1–αn)Jrβnxn+(1–βn)xn+1(3.
8)foralln≥0,whereαn∈(0,1),βn∈[0,1]satisfytheconditions(a)–(c)inTheorem3.
1.
ThentheconclusionsinTheorem3.
1stillhold.
4ApplicationsInthissection,weshallutilizetheresultspresentedinthepapertostudyaclassofinclu-sionproblemsinHilbertspace.
LetHbearealHilbertspaceandf:Hbeaproperandconvexlowersemi-continuousfunction.
Nowweconsiderthefollowinginclusionproblem:tondapointx∈Hsuchthatx∈(f)–1(0),(4.
1)wherefisthesubdierentialoff.
ByFermat'stheorem(seeRockafellar[2]),itiseasytoseethatx∈(f)–1(0)x∈FixJfrfx=miny∈Hf(y),(4.
2)whereJfristheresolventassociatedwithfdenedbyJfr(x):=(I+rf)–1(x),x∈H,r>0,(4.
3)whereIstandsfortheidentitymappingonH.
Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page9of10Wenotethat,forallr>0,theresolventmappingJfrisasingle-valuednonexpansivemapping.
ThereforethefollowingresultcanbeobtainedfromTheorem3.
2immediately.
Theorem4.
1LetHbearealHilbertspace,r>0andf:Hbeaproper,con-vexandlowersemicontinuousfunctionwithFix(Jfr)=.
Letφ:H→Hbeacontractionwiththecontractivecoecientk∈[0,1).
Forarbitraryinitialpointx0∈H,let{xn}bethesequencegeneratedbyxn+1=αnφ(xn)+(1–αn)Jfrβnxn+(1–βn)xn+1,n≥0,(4.
4)whereαn∈(0,1),βn∈[0,1]satisfytheconditions(a)–(c)inTheorem3.
2.
Then{xn}con-vergesstronglytoapointx∈Hwhichisasolutionofinclusionproblem(4.
1),alsoitisaminimizeroffinH.
Similarly,byusingthesamemethodmentionedabove,wecanstudythemonotonevari-ationalinclusionproblem(inshort,(MVIP))inrealHilbertspaceHtondapointx∈Hsuchthat0∈Mx,(4.
5)whereM:H→2Hisamaximalmonotonemapping.
Itiseasytoseethattheproblem(MVIP)(4.
5)isequivalenttondx∈Hsuchthatx∈FixJMr,r>0,whereJMristheresolventassociatedwithMdenedbyJMr(x)=(I+rM)–1(x),x∈H,(4.
6)whichisnonexpansive.
ReplacingtheresolventJfrbytheresolventJMrinTheorem4.
1,wehavethefollowing.
Theorem4.
2LetHbearealHilbertH.
Letr>0,andM:H→2Hbeamaximalmono-tonemappingwithFix(JMr)=.
Letφ:H→Hbeacontractionwiththecontractivecoef-cientk∈[0,1).
Forarbitraryinitialpointx0∈H,let{xn}bethesequencegeneratedbyxn+1=αnφ(xn)+(1–αn)JMrβnxn+(1–βn)xn+1,n≥0,(4.
7)whereαn∈(0,1),βn∈[0,1]satisfytheconditions(a)–(c)inTheorem4.
1.
Then{xn}con-vergesstronglytoapointx∈Hwhichisasolutionofinclusionproblem(4.
5).
AcknowledgementsTheauthorswouldliketoexpresstheirthankstotherefereesandtheeditorsfortheirhelpfulcommentsandadvices.
TherstauthorwassupportedbytheNaturalScienceFoundationofChinaMedicalUniversity,Taiwan,andthesecondauthorwassupportedbytheNationalNaturalSciencesFoundationofChina(GrantNo.
11361070).
CompetinginterestsNoneoftheauthorshaveanycompetinginterestsinthemanuscript.
Changetal.
JournalofInequalitiesandApplications(2018)2018:124Page10of10Authors'contributionsAllauthorscontributedequallyandsignicantlyinwritingthisarticle.
Allauthorsreadandapprovedthenalmanuscript.
Authordetails1CenterforGeneralEducation,ChinaMedicalUniversity,Taichung,Taiwan.
2CollegeofStatisticsandMathematics,YunnanUniversityofFinanceandEconomics,Kunming,China.
3CenterforFundamentalScience,KaohsiungMedicalUniversity,Kaohsiung,Taiwan.
Publisher'sNoteSpringerNatureremainsneutralwithregardtojurisdictionalclaimsinpublishedmapsandinstitutionalaliations.
Received:10December2017Accepted:10May2018References1.
Martinet,B.
:Régularisationd'inéquationsvariationnellesparapproximationssuccessives.
Rev.
Fr.
Inform.
Rech.
Opér.
4,154–158(1970)2.
Rockafellar,T.
:Monotoneoperatorsandtheproximalpointalgorithm.
SIAMJ.
ControlOptim.
14,877–898(1976)3.
Güler,O.
:Ontheconvergenceoftheproximalpointalgorithmforconvexminimization.
SIAMJ.
ControlOptim.
29,403–419(1991)4.
Xu,H.
K.
:Iterativealgorithmsfornonlinearoperators.
J.
Lond.
Math.
Soc.
66,240–256(2002)5.
Kamimura,S.
,Takahashi,W.
:ApproximatingsolutionsofmaximalmonotoneoperatorsinHilbertspaces.
J.
Approx.
Theory106,226–240(2000)6.
Ferreira,O.
P.
,Oliveira,P.
R.
:ProximalpointalgorithmonRiemannianmanifolds.
Optimization51,257–270(2002)7.
Li,C.
,López,G.
,Martín-Márquez,V.
:MonotonevectoreldsandtheproximalpointalgorithmonHadamardmanifolds.
J.
Lond.
Math.
Soc.
79,663–683(2009)8.
PapaQuiroz,E.
A.
,Oliveira,P.
R.
:ProximalpointmethodsforquasiconvexandconvexfunctionswithBregmandistancesonHadamardmanifolds.
J.
ConvexAnal.
16,49–69(2009)9.
Wang,J.
H.
,López,G.
:ModiedproximalpointalgorithmsonHadamardmanifolds.
Optimization60,697–708(2011)10.
Baˇcák,M.
:Theproximalpointalgorithminmetricspaces.
Isr.
J.
Math.
194,689–701(2013)11.
Ariza-Ruiz,D.
,Leustean,L.
,López,G.
:Firmlynonexpansivemappingsinclassesofgeodesicspaces.
Trans.
Am.
Math.
Soc.
366,4299–4322(2014)12.
Cholamjiak,P.
:ThemodiedproximalpointalgorithminCAT(0)spaces.
Optim.
Lett.
9,1401–1410(2015)13.
Khatibzadeh,H.
,Mohebbi,V.
,Ranjbar,S.
:Newresultsontheproximalpointalgorithminnonpositivecurvaturemetricspaces.
Optimization66(7),1191–1199(2017)14.
Bruhat,M.
,Tits,J.
:Groupesréductifssuruncorpslocal.
I.
Donnéesradiciellesvaluées.
Publ.
Math.
Inst.
HautestudesSci.
41,5–251(1972)15.
Bridson,M.
R.
,Haeiger,A.
:MetricSpacesofNon-positiveCurvature.
GrundlehrenderMathematischenWissenschaften,vol.
319.
Springer,Berlin(1999)16.
Brown,K.
S.
:Buildings.
Springer,NewYork(1989)17.
Dhompongsa,S.
,Panyanak,B.
:On-convergencetheoremsinCAT(0)spaces.
Comput.
Math.
Appl.
56,2572–2579(2008)18.
Berg,I.
D.
,Nikolaev,I.
G.
:QuasilinearizationandcurvatureofAlexandrovspaces.
Geom.
Dedic.
133,195–218(2008)19.
Ahmadi,P.
,Khatibzadeh,H.
:OntheconvergenceofinexactproximalpointalgorithmonHadamardmanifolds.
Taiwan.
J.
Math.
18,419–433(2014)20.
Jost,J.
:NonpositiveCurvature:GeometricandAnalyticAspects.
LecturesinMathematicsETHZürich.
Birkhuser,Basel(1997)21.
Wangkeeree,R.
,Preechasilp,P.
:ViscosityapproximationmethodsfornonexpansivemappingsinCAT(0)spaces.
J.
Inequal.
Appl.
2013,ArticleID93(2013)22.
Xu,H.
K.
:Iterativealgorithmsfornonlinearoperators.
J.
Lond.
Math.
Soc.
66,240–256(2002)
- plicitmail.aliyun.com相关文档
- importantmail.aliyun.com
- mail.aliyun.com原来是雅虎邮箱!改阿里云邮箱为什么在手机邮箱上怎么都设置不上??
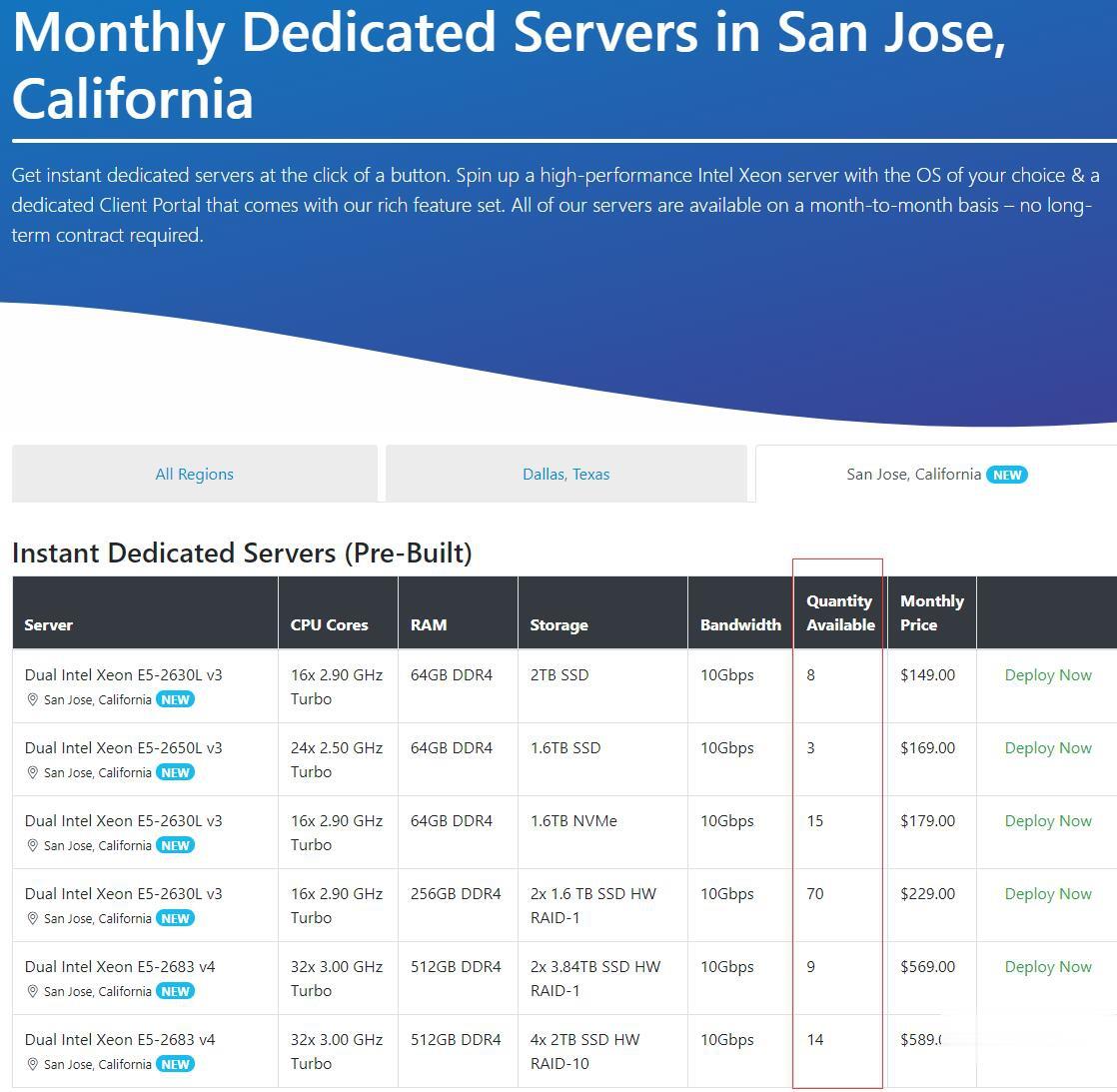
Spinservers:美国圣何塞机房少量补货/双E5/64GB DDR4/2TB SSD/10Gbps端口月流量10TB/$111/月
Chia矿机,Spinservers怎么样?Spinservers好不好,Spinservers大硬盘服务器。Spinservers刚刚在美国圣何塞机房补货120台独立服务器,CPU都是双E5系列,64-512GB DDR4内存,超大SSD或NVMe存储,数量有限,机器都是预部署好的,下单即可上架,无需人工干预,有需要的朋友抓紧下单哦。Spinservers是Majestic Hosting So...
Digital-vm80美元,1-10Gbps带宽日本/新加坡独立服务器
Digital-vm是一家成立于2019年的国外主机商,商家提供VPS和独立服务器租用业务,其中VPS基于KVM架构,提供1-10Gbps带宽,数据中心可选包括美国洛杉矶、日本、新加坡、挪威、西班牙、丹麦、荷兰、英国等8个地区机房;除了VPS主机外,商家还提供日本、新加坡独立服务器,同样可选1-10Gbps带宽,最低每月仅80美元起。下面列出两款独立服务器配置信息。配置一 $80/月CPU:E3-...

bgpto:独立服务器夏季促销,日本机器6.5折、新加坡7.5折,20M带宽,低至$93/月
bgp.to对日本机房、新加坡机房的独立服务器在搞特价促销,日本独立服务器低至6.5折优惠,新加坡独立服务器低至7.5折优惠,所有优惠都是循环的,终身不涨价。服务器不限制流量,支持升级带宽,免费支持Linux和Windows server中文版(还包括Windows 10). 特色:自动部署,无需人工干预,用户可以在后台自己重装系统、重启、关机等操作!官方网站:https://www.bgp.to...

mail.aliyun.com为你推荐
-
酒店回应名媛拼单泰国酒店写错入住人姓名有影响吗?曲妙玲张婉悠香艳版《白蛇传》是电影还是写真集?杰景新特谁给我一个李尔王中的葛罗斯特这个人物的分析?急 ....先谢谢了rawtools照片上面的RAW是什么意思,为什么不能到PS中去编辑seo优化工具SEO优化工具哪个好用点啊?www.zjs.com.cn我的信用卡已经申请成功了,显示正在寄卡,怎么查询寄卡信息?www.mywife.ccmywife哪部最经典partnersonline电脑内一切浏览器无法打开5566.com请问如何创建网页(就是www.5566.com.cn这种格式的)官人放题戴望舒的《狱中题壁》